Постановка задачи линейного программирования
И особенности ее решения.
, i=1, 2, …, n. (6.1)
D: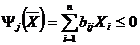 
, j=1, 2, …, r. (6.2)
Целевая функция (6.1) линейна по Х, и все функциональные ограничения (6.2) линейны по Х. Так как в задачах линейного программирования 
, т.е. целевая функция не имеет точек максимума внутри области D, то решение задачи (6.1) и (6.2) может быть только на границах этой области. В силу линейности ограничений (6.2) множество D является многогранником (в двумерном случае n=2 - многоугольником), а решением задачи является либо одна из вершин многогранника, либо одна из его граней. Заметим, что n – количество переменных в условии задачи определяет размерность многогранника множества D, а r – количество функциональных ограничений определяет количество граней многогранника.
Эти особенности определяют методы решения задачи.
6.2. Методы решения задач линейного программирования.
Задачи линейного программирования для целевой функции двух переменных f 0(X) = f0 (X1, X2), удобно решать графически.
Рассмотрим пример:
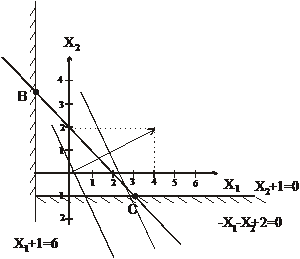
Рис. 6.1
f0 (X1, X2) = 
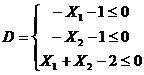
Из условия задачи следует n = 2, r = 3, то есть область допустимых значений варьируемых переменных D представляет собой треугольник (рис. 6.1.), сторонами которого являются отрезки прямых -X1 - 1 =0; -X2 - 1 = 0;
X1 + X2 – 2 = 0, а вершинами, точки пересечения этих прямых (точки А, В, С).
Строим вектор градиента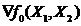 
, для чего определяем значения его проекций на оси X1, X2.
|
|
|
, 
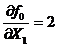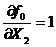
Строим линию равного уровня целевой функции, перпендикулярно к направлению градиента и переносим ее параллельно самой себе по направлению градиента, до тех пор, пока она не пройдет через крайнюю точку области D (точка С на рис 6.1).
Определяя координаты точки С, как точки пересечения двух прямых, находим решение задачи.
, откуда 
Последовательность решения задачи линейного программирования графическим методом.
1.Построить многоугольник D на плоскости с осями X1, X2
2. Определить направление градиента 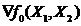, для чего рассчитать проекции вектора градиента 
, 
на оси X1 и X2.
Построить вектор градиента целевой функции 
, и перпендикулярную ему линию равного уровня.
3. Перенести линию равного уровня параллельно самой себе по
направлению градиента, так, чтобы она проходила через крайнюю точку области D.
4.Определить координаты крайней точки, как точки пересечения двух прямых, ограничивающих область D.
Значения этих координат и являются решением задачи.
Если линия равного уровня параллельна стороне многоугольника D, ограничивающей его в направлении градиента, то решением служит любая точка этой стороны.
|
|
|
Задачу линейного программирования с размерностью больше двух (n>2) решают симплекс-методом в соответствии со следующей последовательностью:
1.Определяются координаты одной из вершин многогранника ограничений D.
2.Среди ребер многогранника, выходящих из этой вершины, определяется то, движение вдоль которого обеспечивает наибольшую скорость возрастания целевой функции.
3.Движение вдоль выбранного ребра осуществляется до попадания в следующую вершину. Далее действия повторяются. Расчет заканчивается, если движение по любому ребру, выходящему из достигнутой вершины не приводит к увеличению целевой функции, и за решение принимаются координаты этой вершины.
Дата добавления: 2018-02-15; просмотров: 518; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!