Свертка частных критериев с весовыми коэффициентами.

⇐ ПредыдущаяСтр 17 из 21Следующая ⇒

В этом случае сводный критерий I представляет собой сумму частных критериев , умноженных на соответствующие весовых коэффициенты .

Весовые коэффициенты учитывают относительную важность того или иного критерия и устанавливаются путем экспертизы для конкретной задачи оптимизации. Причем их значения должны лежать в переделах от нуля до единицы, а их сумма равняться единице.

Математическая постановка задачи:

(8.1)

где ; (8.2)

Значения частных критериев при формировании сводного критерия должны быть либо безразмерными, либо иметь одинаковую размерность, для того, чтобы их суммирование имело смысл.

Геометрически, применение критерия (8.1) приводит к выбору на множестве I такого вектора у которого максимальна проекция на прямую γ, такую, что квадраты ее направляющих косинусов равны , в .частности

Использование нормативных критериев.

Пусть для каждого из частных критериев известно некоторое нормативное значение , например среднее значение I_υ для действующих аппаратов, аналогичных оптимизируемому.

Тогда отношение характеризует степень совершенства процесса с точки зрения υ - го показателя. Обозначим минимальное по υ значение через . В этом случае величина может быть критерием оптимизации, т.е.

(8.3)

В этом случае задача оптимизации состоит в максимизации того относительного частного показателя качества , который имеет наименьшее значение.

При использовании критерия (8.3) можно быть уверенным, что степень совершенства оптимизируемого процесса по любому показателю будет не ниже, чем величина , полученная в результате решения задачи (8.3).

Практически часто оказывается, что увеличение одного из показателей приводит к уменьшению другого. В этом случае использование критерия (8.3) дает такое оптимальное решение , для которого два или несколько значений окажутся одинаковыми и равными значению , полученному в результате решения задачи.

Приближение к идеалу.

Пусть известны решения m задач оптимизации вида

; υ=1, …, m (8.4)

В результате найдены предельные значения каждого из частных критериев оптимальности без учета остальных. В пространстве критериев точку с координатами называют идеалом. Когда решения задач (8.1) не одинаковы, идеал не принадлежит множеству допустимых значений критериев (см. рис. 8.1).

Однако можно на втором этапе решения поставить задачу определения такого достижимого критерия и соответствующего ему допустимого решения , для которых расстояние от идеала было бы минимальным, например

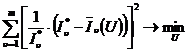(8.5) или

(8.6)

В случае выбора критерия (8.5) минимизируется квадрат расстояния от достижимой оптимальной точки на плоскости критериев до точки идеала I^*, при выборе критерия (8.6) минимизируется максимальное из расстояний от получаемой точки до точек максимума по частным критериям I₁^* или I₂^*.

Справедливый компромисс.

Выбор решения в задаче с несколькими частными критериями представляет собой компромисс, т.к. увеличение одного показателя качества часто приводит к уменьшению другого. При справедливом компромиссе стремятся к тому, чтобы в точке сумма относительных изменений всех показателей была равна нулю, т.е. в точке должно быть выполнено равенство

(8.7)

Это равенство можно преобразовать к виду

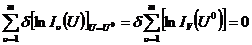(8.8)

Равенство (8.8) является необходимым условием максимума произведений , т.е. справедливый компромисс соответствует сводному критерию

(8.9)

Заканчивая рассматривать способы формирования сводных критериев оптимальности отметим, что одним из самых распространенных способов увязки частных критериев является формирование критерия оптимальности в экономических терминах.

Оптимальность по Парето.

Выбор любого сводного критерия субъективен или основан на некоторых дополнительных предположениях. Однако оптимальное решение в задаче с несколькими критериями можно получить без введения сводного критерия. Такой подход был предложен в 1904 г. итальянским экономистом В. Парето.

Оптимальным по Парето решением Uп является любое решение, если среди допустимых решений не найдётся такого U^О, для которого:

I_υ(U^O) ³ I_υ(U_п) υ= 1,…,m (8.10)

причём хотя бы для одного значения υ неравенство (8.10) строгое. Иными словами, U_п оптимально, если, изменяя его, нельзя улучшить ни одного из частных показателей, не ухудшая при этом хотя бы одного из остальных.

Оптимальным, по Парето, решениям соответствует на рис. 8.1 та часть границы множества I (выделена жирной линией), для которой любое направление движения, образующее с осью абсцисс угол от 0 до p/2, выходит за пределы множества I, например, точка I_п1.

Можно доказать, что любой из приведённых выше способов образования сводного критерия I приводит к получению одного из решений, оптимальных по Парето. В том случае, когда граница множества I, соответствующая оптимальным по Парето решениям, выпукла, все эти решения можно получить из задачи о максимуме сводного критерия (8.1) при изменении весовых коэффициентов g_υ, т.е. в пределах условий (8.2).

Действительно, для рис. 8.1 в соответствии с выражениями (8.1) и (8.2) имеем:

В случае , , 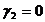получаем , а при , . Очевидно, что при уменьшении от единицы до нуля и соответствующем увеличении от нуля до единицы точка будет перемещаться по границе множества I от точки до точки .

Дата добавления: 2018-02-15; просмотров: 809; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 12 13 14 15 161718 19 20 21 Следующая ⇒

Мы поможем в написании ваших работ!