Численные методы решения задачи. (методы одномерного поиска).
(методы одномерного поиска).
Методы одномерного поиска представляют собой вычислительную процедуру, в ходе которой интервал возможных значений 
изменяется от заданного начального до конечного, не превышающего допустимую погрешность.
При использовании этих методов вычисляется значение целевой функции при 
, 
выбирается таким образом, чтобы 
, где i – номер шага поиска.
Алгоритм поиска должен включать в себя:
- правило перехода от 
к ,
- правило окончания поиска, которое связано с точностью определения , т.е. с величиной заданной допустимой погрешности.
Численные методы решения оптимизационных задач в основном представляют из себя итерационные вычислительные процедуры. Суть итерационных методов расчета заключается в том, что на каждой последующей итерации (этапе) расчета используются результаты, полученные на предыдущей итерации.
В оптимизационных задачах результаты предыдущей итерации используются для того, чтобы уменьшить область (для задач одномерного поиска-интервал), в которой будет искаться максимум на последующей итерации.
К неитерационным методам, где расчеты осуществляются в один этап, относятся методы, позволяющие работать с невыпуклыми функциями, имеющими несколько точек максимума. Одним из таких методов является метод равномерного поиска, рассматриваемый ниже.
Метод равномерного поиска
Пусть 
целевая функция, определенная на D: 
, необходимо найти 
с допустимой погрешностью e (рис. 2.5)
|
|
|
Рис. 2.5
|
делится на m равных отрезков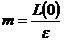 
. Если 
, т.е. ошибка задана не в абсолютных единицах, а в относительных и представляет собой определенную часть от длины исходного интервала L(0) , то 
, 
- число узловых точек.
После этого производится вычисление значений целевой функции 
во всех узловых точках и сравнивание их между собой. За решение задачи принимается значение Х в узловой точке с наибольшим значением целевой функции.
Недостатком метода является его громоздкость, например при 
, что соответствует вычислению максимума с точностью 0,1% от величины исходного интервала неопределенности, число вычислений целевой функции, равное числу узлов 
. Преимуществом же данного метода, как отмечалось выше, является его пригодность к вычислению глобального максимума невыпуклых, или, по другому, не унимодальных функций.
Ниже приведенные итерационные методы одномерного поиска, пригодны только для определения максимума выпуклых (унимодальных) функций.
Дата добавления: 2018-02-15; просмотров: 897; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!