Определение безусловного максимума функции нескольких переменных.

Постановка задачи и ее геометрическая интерпретация.

Линии равного уровня.

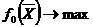 (3.1). по вектору , где  и область допустимых значений V задана условиями  (3.2).

Заметим, что в дальнейшем все области допустимых значений варьируемых переменных, задаваемые только в виде автономных ограничений  (3.2) будем обозначать буквой V, а области, где присутствуют ограничения типа связи и (или) функциональные ограничения по-прежнему буквой D.

Таким образом по постановке задачи сразу можно будет отличать задачу на нахождение целевого максимума , от задачи на нахождение безусловного максимума .

                                        Рис. 3.1.

 

Рассмотрим  - функция двух переменных (рис. 3.1). Для ее изображения необходимо трехмерное пространство, что неудобно. Поэтому функцию двух переменных обычно изображают на плоскости варьируемых переменных X₁, X₂ в виде линий равного уровня (рис. 3.2). Координаты X₁ и X₂ любой точки линии равного уровня дадут одно и то же значение целевой функции . Внутри линий равного уровня отображается точка максимума M. Чем ближе расположена линия равного уровня к точке максимума, тем большему значению целевой функции она соответствует. Так на рисунке 3.1 имеем С₂ > С₁.

Задавая границы  и  i=1,2 получаем множество допустимых значений варьируемых переменных V в виде прямоугольника (рис. 3.2).

Рис. 3.2

Если  в V имеет единственный max, то функция выпукла, иначе может быть несколько решений (локальных максимумов - точки М₁ и М₂ на рис. 3.3), среди которых необходимо выбрать наибольшее (глобальный максимум).

Методы определения максимума здесь также делятся на аналитические и численные.

                    Рис. 3.3

 

Аналитический метод решения задачи.

 Аналитический метод использует необходимое условие max функции нескольких переменных:

Для того чтобы в точке  функция 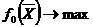, необходимо, чтобы (3.3), для всех i=1,2…n.                                    Для выделения точек максимума необходимо также проверить знаки диагональных миноров матрицы вторых производных (матрицы Гессе).

В общем случае:

                                                    (3.4)

Для функции двух переменных:

                                                                          (3.5)

                                                                 (3.6)    

где - главный определитель матрицы.

В зависимости от знака D возможны три случая:

1) D < 0 – экстремум отсутствует, точка перегиба,

2) D = 0 – требуется дополнительное исследование,

3) D > 0 – экстремум есть, причем в случае

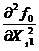 < 0 и  < 0, это max, а при 

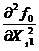 > 0 и > 0 – min.

 

Пример.

 Определить максимум функции

;

                                   

Откуда ,

< 0

< 0    ,

откуда  > 0, т.е. ,  - точка max, т.к. 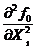 < 0 и  < 0.

 

Численные методы решения задачи

(методы многомерного поиска).

Численные методы многомерного поиска будем рассматривать на примере нахождения максимума функции двух переменных. Такие функции, как показано выше (раздел 3.1.), изображаются на плоскости  в виде линий  равного уровня.

Наложение автономных ограничений на переменные  приводит к выделению на плоскости области допустимых решений V в виде прямоугольника(рис. 3.4).

---

Дата добавления: 2018-02-15; просмотров: 577; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!