Оптимизация статического установившегося режима.
Большую часть времени аппараты работают в установившемся режиме. Этот режим может быть статическим (когда все переменные, характеризующие его, неизменны во времени) или циклическим (когда все переменные или часть из них периодически изменяются).
В статическом режиме при каждом значении вектора внешних воздействий (состав сырья, параметры окружающей среды и т.п.) нужно найти такие управления, чтобы показатель эффективности работы аппарата был максимален, т.е.
¦0 ( 
, 
) ® max (9.7)
при автономных ограничениях (9.2), функциональных ограничениях (9.5) и связях между X и U, определяемых статическими характеристиками аппарата
¦n ( , ) = 0 n = 1,…, m (9.8)
Также возможны ограничения на общий ресурс управляющих воздействий за весь период функционирования типа (9.6).
В этой задаче и уже не вектор–функции, зависящие от t, как в разделах (9.1), (9.2), а просто вектора.
Если целевые функции, определяющие задачу, непрерывны по совокупности переменных, то оптимизация статического режима представляет собой задачу нелинейного программирования.
Оптимизация циклического установившегося режима.
Для циклических режимов критерием оптимальности является среднее значение целевой функции ¦0 за период цикла T:
I = 
dt ® max (9.9)
|
|
|
Связи между переменными состояния и управляющими воздействиями характеризуют динамику процесса и имеют форму дифференциальных уравнений (9.4), автономные ограничения (9.2) остаются в силе, а ограничения на ресурс управляющих воздействий задаются в среднем за цикл, т.е.
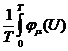dt - bm = 0 m = 1, …, r (9.10)
Они могут соответствовать ограничениям на средний расход сырья, электрической энергии и т.п.
Краевые условия типа (9.3) для дифференциальных уравнений (9.4) в циклическом режиме, как правило, не фиксированы, однако ввиду непрерывности переменных и их периодичности справедливы равенства:
Xn(T) = Xn(0) n = 1,…m (9.11)
что эквивалентно требованиям
dt = 0 n = 1,…, m (9.12)
В этой задаче кроме законов изменения управляющих переменных и связанных с ними переменных состояния, нужно ещё оптимально выбрать длительность цикла T.
Часто форму изменения управляющих воздействий задают с точностью до нескольких параметров. Например, считают их синусоидальными. Тогда нужно найти амплитуды и средние значения управляющих переменных, а также фазовые сдвиги между ними.
|
|
|
Оптимизация режима в аппарате периодического действия.
Здесь сырьё периодически загружают в аппарат, а готовый продукт периодически выгружают из него. Продолжительность цикла, а также закон изменения управляющих воздействий за время цикла подлежат оптимальному выбору.
Пусть целевая функция ¦0( , ) определяет мгновенную продуктивность процесса.
Обозначим через q - продолжительность загрузки и выгрузки, а T – продолжительность работы аппарата в каждом цикле. Учтём также, что загрузка и выгрузка связаны не только с затратами времени, но и с затратами трудовых и материальных ресурсов на сырьё, очистку аппарата и т.д. Величину этих затрат, которые обычно не зависят от длительности цикла, обозначим через А.
Тогда критерий оптимальности задачи запишется в виде:
I = 
dt – А ) ® max (9.13)
Максимум этого выражения нужно найти при условиях (9.4), записанных в форме дифференциальных уравнений и при фиксированных начальных значениях переменных состояния.
Xn(0) = Xn0 n = 1,…, m (9.14)
Что касается конечных значений этих переменных Xn(T), то, как правило, некоторые из них фиксированы, а остальные свободны.
|
|
|
Xn(T) = XnT n = 1,…, k; k < m (9.15)
Условия типа автономных ограничений (9.2) и функциональных ограничений (9.5) также могут иметь место. Выбору подлежат управляющие воздействия (t) и рабочее время цикла T.
Календарное планирование работы аппарата
В предыдущих задачах предполагалось, что собственные характеристики аппарата и условия, в которых он работает, неизменны. В действительности же и те и другие могут изменяться во времени. Например, по некоторому закону могут изменяться заданная производительность и поставки сырья. Как правило, эти изменения происходят значительно медленнее, чем переходные процессы в аппарате, поэтому связи между состояниями X и управлениями U задают в квазистатической форме.
¦n( , , t) = 0 n = 1,…, m (9.16)
Производительность аппарата для каждого момента времени t должна лежать в заданном интервале
P*(t) £ P ( , ) £ P*(t) (9.17)
Если в аппарате имеются ёмкости, то на уровень в них наложены ограничения Hi* £ Hi (t) £ Hi* " t
·
Hi = hi ( , , t) i = 1,…, l, (9.18)
|
|
|
где hi ( , , t) – разность потоков, втекающих в i-ю ёмкость и вытекающих из неё в момент t.
Если через Tn обозначить интервал планирования, то критерием оптимальности может служить интегральная эффективность аппарата за этот интервал.
I = 
dt ® max (9.19)
Оптимальный режим работы
Дата добавления: 2018-02-15; просмотров: 515; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!