Параллельно включенных агрегатов: распределение нагрузок.

Задача формулируется следующим образом (рис.9.1):

Рис. 9.1. Рис. 9.2.

– требуется выбрать нагрузку каждого из агрегатов и состав работающих агрегатов, включённых параллельно, если общая нагрузка (суммарный расход сырья) задана, а общая производительность должна быть максимальной.

С= ,

где X_i – нагрузка на каждый агрегат i=1,2…n, С – суммарная нагрузка,

Р= ,

где Р_i – производительнлсть i-го агрегата i=1,2…n, Р – суммарная производительность.

Для каждого из агрегатов известна нагрузочная характеристика – зависимость производительности P_i от расхода сырья X_i (рис. 9.2).

Тогда критерий оптимальности запишется в виде:

P = (X_i) ® max (9.20)

а ограничения X_i = 0 или X_i_*£ X_i £ X_i^*.

Первое из этих условий относится к случаю, когда агрегат выключен, а второе – когда он работает. Эти условия удобно переписать, исключив слово «или», для чего вводится целочисленная переменная Vi.

V_i=

Обозначив X_i = V_i 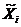, получаем критерий оптимальности

P = ® (9.21)

V_i= 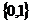, i=1…n (9.22)

D= (9.23)

Условие (9.23) соответствует выполнению требования суммарной нагрузки по сырью. Наличие целочисленных переменных значительно усложняет решение этой задачи. Рассмотрим некоторые варианты постановки задачи распределения.

Минимизация затрат.

Пусть задан не суммарный расход сырья, а суммарная производительность P. Нужно выбрать состав и нагрузки действующих агрегатов, чтобы суммарные затраты были минимальны.

При этом затраты, связанные с i-м агрегатом, определяются в общем случае не только затратами на сырьё Ц 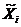, где Ц – стоимость единицы сырья, но и амортизационными отчислениями, зависящими от стоимости агрегата Аi и коэффициента амортизационных отчислений К. Величина Аi может включать и стоимость обслуживания i-го агрегата.

Задача примет вид

I= 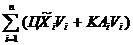®min

При этом нужно учесть ограничения (9.23).

Учет вероятностного характера нагрузки.

В некоторых случаях величину суммарного расхода сырья С следует считать случайной. Например, в системе параллельно работающих печей задан суммарный расход топлива. Однако, нагрузочная характеристика учитывает не расход топлива, а количество тепла, поступающего в печь с топливом. Таким образом С в условии (9.23) представляет собой суммарный расход энергии топлива, зависящий от его состава, который оперативно не измеряют или измеряют с большой ошибкой. В этом случае решение должно быть оптимально в среднем, на множестве возможных значений энергии, выделяемой единицей топлива, с учётом их вероятности.

Учёт динамических факторов.

Нагрузочная характеристика часто бывает определена не для всех значений X_i (см. рис. 9.2).

В частности, агрегат не может работать на отрезке [0 - X_i_*], поэтому не каждое значение суммарной производительности, можно обеспечить, даже установив несколько агрегатов. В таких случаях может оказаться необходимым использование промежуточных емкостей (рис. 9. 3).

Рис. 9.3.

Производительность агрегата P(t) при такой схеме может периодически меняться и быть то больше, то меньше заданной , которая остается неизменной. При таком построении необходимо учесть ограничения на степень заполнения каждой ёмкости.

Переход к периодической производительности, которая в среднем равна заданной, может оказаться выгодней и в экономическом отношении.

Действительно, если часть периода агрегат работает при нагрузке X_i ^*, а оставшуюся часть периода выключен, причём время работы выбрано так, что средний расход сырья за период равен X_i_*, то при определённых формах нагрузочной кривой может быть получена средняя за период производительность

_i(X_i^*) > P_i (X_i_*) – т.е. больше агрегата, работающего весь период при минимально допустимой нагрузке, причем расход сырья в обоих случаях будет одинаков.

Так, например, если для нагрузочной кривой, представленной на рис. 9.2, примем X_i_* = 5, X_i^* = 10, P_i (X_i_*) = 1 P_i (X_i^*) = 4 и период работы Т = 10, то, в случае работы агрегата весь период при минимальной нагрузке X_i_* , имеем количество получаемого продукта S₁ = P_i (X_i_*) × T = 1 × 10 = 10 единиц,

при расходе сырья X_iT = X_i_*× T = 5 × 10 = 50 единиц,

а в случае работы агрегата полпериода при максимальной нагрузке имеем количество продукта S₂ = P_i (X_i^*) × 0, 5 × T = 4 × 0, 5 × 10 = 20 единиц,

при расходе сырья X_i_0,5_T = X_i^* × 0, 5 × T = 10 × 0, 5 × 10 = 50 единиц.

Таким образом, второй режим работы агрегата позволяет удвоить выход продукции без увеличения расхода сырья.

Дата добавления: 2018-02-15; просмотров: 554; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 12 13 14 15 16 17 18 192021 Следующая ⇒

Мы поможем в написании ваших работ!