Закон парности касательных напряжений.
Выясним, каковы касательные напряжения по площадке перпендикулярной данной, т.е. задаваемой углом 
т.е. 
Знак “минус” указывает на то, что касательные напряжения на взаимно перпендикулярных площадках направлены либо к ребру между площадками либо от ребра. Таким образом имеет местозакон парности касательных напряжений: Касательные напряжения по взаимно перпендикулярным площадкам равны по величине и направлены как было указано выше.
Коэффициент запаса. Допускаемые напряжения.
Состояния, при которых происходят коренные изменения механического состояния материала в точке, называется предельным.
Различают два предельных состояния:
1) Переход материала в пластическое состояние, т.е. появление значительных остаточных деформаций.
2) Разрушение. Т.е. рост трещин и распадение на части.
Соответственно сказанному, оценивая состояние конструкции, различают два коэффициента запаса:
а) Коэффициент запаса по текучести 
где
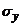- предел текучести;
- максимальное напряжение, возникающее в конструкции.
По данному коэффициенту оцениваются конструкции, выполненные из достаточно пластичных материалов.
б) Если материал конструкции хрупок и обладает незначительными пластическими свойствами, то прибегают к коэффициенту запаса по разрушению 
где
- предел прочности или временное сопротивление.
Иногда коэффициенты запаса выступают в другом качестве: в роли нормативных заданных величин, с помощью которых определяются так называемые допускаемые напряжения:
|
|
|
Допускаемое напряжение;
а) для пластичных материалов определяется 
б) Для хрупких материалов 
Расчет по методу допускаемых напряжений состоит в обеспечении условия: 
, называется условием прочности.
Статически неопределимые системы, работающие на растяжение и сжатие.
Системы, у которых число неизвестных реакций связей превышает число независимых уравнений равновесия, называются статически неопределимыми системами.
В подобных случаях из уравнений статики не могут быть найдены внутренние силовые факторы, а, следовательно, и напряжения для всех элементов системы.
Например, стержень, защемленный одним концом -система статически определимая, однако, защемив второй конец стержня, мы получим систему статически неопределимую, т.к. неизвестных реакций станет 2, а уравнение равновесия, по-прежнему, единственное – сумма всех сил на ось стержня.
Стержневая система, состоящая из двух стержней, соединенных шарнирно – статически определима. Добавляя еще один стержень, мы превращаем ее в статически неопределимую, т.к. неизвестных усилия 3, а система сходящихся сил позволяет составить лишь два независимых уравнения статики.
|
|
|
Определить усилия в подобных системах, находясь в рамках гипотезы абсолютно твердого тела, принципиально невозможно. Выход из положения состоит в том, что нужно рассматривать деформации и перемещения, возникающие в системе.
Общий план решения статически неопределимых задач следующий:
1) Составляем уравнения равновесия.
2) Рассматривая перемещения узлов системы, составляем уравнения связывающие деформации отдельных элементов системы (или удлинения ее элементов). Эти уравнения называют обычно уравнениями совместности деформаций (совместности перемещений).
3) Заменяем в уравнениях совместности деформаций величины деформаций или удлинений через напряжения или усилия по зако-
ну Гука.
4) Решаем полученную линейную систему из уравнений равновесия и уравнений совместности и находим искомые усилия.
Дата добавления: 2018-02-15; просмотров: 547; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!