Теорема о работе статической силы, приложенной к упругой системе (Теорема Клапейрона).
Работа статической силы, приложенной к упругой системе, равняется половине произведения окончательного значения силы на окончательное значение перемещения.
Пусть 
- сила, изменяющаяся на сегменте 
а
- перемещение, изменяющееся в пределах 
. Система линейно упруга и сила связана с перемещением законом Гука 
, где 
- перемещение, вызванное силой 
Тогда
Эта теорема, носящая имя Клапейрона, имеет простую геометрическую интерпретацию.
Легко понять, что множитель у работы, равный 
появляется по той причине, что сила не постоянна, а меняется по линейному закону.
Потенциальная энергия деформации плоской стержневой системы.
Будем рассматривать плоскую систему, т.е. систему все стержни которой и все силы лежат в одной плоскости. В стержнях такой системы в общем случае могут возникать при внутренних силовых факторах: 
Упругая система, деформируясь, накапливает при этом энергию (упругую энергию) называемую потенциальной энергией деформации.
Потенциальная энергия деформации при растяжении и сжатии.
Потенциальная энергия накопленная в малом элементе длиной dz будет равняться работе сил приложенных к этому элементу
Потенциальная энергия для стержня: 
Замечание. 
и 
- необязательно постоянные величины
.Напряженное состояние при растяжении и сжатии.
Во вводной лекции мы уже упоминали о напряженном состоянии в точке и в частности, говорили, что знать напряженное состояние в точке – это уметь вычислить напряжения по любой площадке, проходящей через данную точку. Теперь уже мы рассмотрим этот вопрос в случае, когда исследуемая точка принадлежит растянутому или сжатому стержню.
|
|
|
Пусть стержень растянут силой F и в поперечных сечениях стержня, как мы знаем, возникают нормальные напряжения равные 
, где А - площадь поперечного сечения.
Проведем через исследуемую точку А произвольное сечение, положение которого задается углом 
между осью стержня и внешней нормалью к сечению. Кроме того, проведем еще поперечное сечение. Выделим с помощью указанных сечений элемент и рассмотрим равновесие данного элемента.
По наклонной площадке действует полное напряжение 
. проектируя силы, действующие на элемент на ось стержня, получаем
Разлагая на нормальное 
и касательное напряжение, получаем
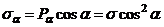
Переходя к функциям угла 
имеем
Уравнения (5) дают возможность вычислить напряжения по любым площадкам, проходящим через данную точку, т.е. определяют напряженное состояние при растяжении и сжатии. Очевидно, что касательные напряжения обращаются в нуль по двум площадкам 
(поперечное сечение) и 
(продольное сечение). Площадки, по которым касательные напряжения равны нулю, называются главными площадками, а нормальные напряжения, действующие по ним, главными напряжениями.
|
|
|
Очевидно, что одно из главных напряжений, действующее в поперечном сечении - 
является максимальным по модулю, что обосновывает использование формулы (1), как основной расчетной формулы при растяжении, сжатии, а другое главное напряжение, действующее в продольных площадках рано нулю. Таким образом, продольные площадки свободны от напряжений.
Из второго уравнения (5) видно, что максимальные касательные напряжения возникают по площадкам, наклоненным к оси на угол 
, и равняются по величине 
Максимальные касательные напряжения являются причиной разрушения образцов из хрупких материалов, испытываемых на сжатие.
Дата добавления: 2018-02-15; просмотров: 1034; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!