ЧИСТЫЙ СДВИГ. КРУЧЕНИЕ СТЕРЖНЕЙ КРУГЛОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ
Напряженное состояние чистого сдвига - одно из простейших
(наряду с растяжением и сжатием) напряженных состояний.
Чистым сдвигом называется плоское напряженное состояние, при котором на гранях элемента возникают одни лишь касательные напряжения.
Грани элементарного параллелепипеда при деформации перекашиваются. С точностью до малого высшего порядка можно считать, что ребра остаются прямыми и длина их не меняется. В таком случае деформированное состояние элемента можно определить с помощью лишь одного параметра – угла сдвига 
, т.е. угла на который изменится первоначально прямой угол между гранями элемента.
Напряженное состояние чистого сдвига может быть реализовано при кручении тонкостенной трубы круглого сечения.
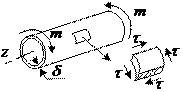При сравнительно небольших деформациях для большинства материалов можно считать, что угол сдвига пропорционален касательному напряжению, т.е. имеет место закон Гука при чистом сдвиге: 
(1)
G – модуль сдвига, или как его еще называют модуль упругости второго рода. Он связан с двумя другими упругими постоянными модулем упругости при растяжении-сжатии и коэффициентом Пуассона следующим соотношением:
Для сталей среднее значение упругих постоянных:
Определим главные напряжения при чистом сдвиге. Т.к. положение одной из главных площадок известно, то два других главных
напряжения можно определить по формуле (4) лекции 17 прошлого семестра. 
= 
; 
|
|
|
Т.к. 
имеют разные знаки, то очевидно, что чистый
сдвиг - смешанное плоское напряженное состояние.
Кручение.
Кручением называется такое нагружение стержня, когда в поперечных сечениях стержня возникает лишь один внутренний силовой фактор – крутящий момент.
Эпюры крутящих моментов строятся аналогично эпюрам изгибающих моментов и нормальных сил.
Правило знаков для моментовможет принято следующее: если при взгляде со стороны внешней нормали крутящий момент (внутренний) направлен против часовой стрелки, то крутящий момент считается положительным.
Кручение стержней круглого поперечного сечения.
Будем рассматривать случай (так называемого) нестесненного кручения, когда деформации стержня в направлении его оси не затруднены. В таком случае в поперечных сечениях стержня возникают только касательные напряжения. Этот факт можно принять за первое допущение, используемое нами в дальнейшем выводе.
Второе допущение имеет геометрический характер и состоит в том, что поперечные сечения при кручении остаются плоскими и их радиусы не искривляются.
Как показывает точное решение задачи методами теории упругости, для круглых поперечных сечений эта гипотеза выполняется абсолютно точно.
|
|
|
Нашей задачей будет определение напряжений и перемещений в закручиваемом стержне.
Рассмотрим произвольный стержень круглого поперечного сечения.
Выделим кольцеобразный малый элемент, а из него в свою очередь элемент m, npо который в пределе
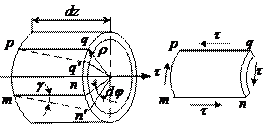можно считать плоским. Данный элемент содержит точку, напряженное состояние которой мы исследуем. Полярный радиус исследуемой точки 
.
Основываясь на первом принятом допущении, заключаем, что элемент mnpq испытывает чистый сдвиг.
Рассмотрим геометрическую сторону задачи.
При кручении поперечные сечения, между которыми заключен элемент повернутся друг относительно друга на малый угол d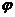 
. Очевидно, что угол сдвига будет равен 
.
Величину 
называем относительным углом закручивания. 
Тогда 
(1).
Рассмотрим физическую сторону задачи. Будем полагать материал линейно упругим и примем закон Гука 
(2).
Подставим (1) в (2): 
(3).
Мы видим, что касательные напряжения по радиусу меняются линейно, но величина Q нам еще не известна.
Обратимся к статической стороне задачи и рассмотрим равновесие отсеченной части стержня 
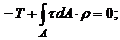
Интеграл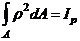 
- полярный момент инерции.
|
|
|
В результате получаем так называемую основную зависимость при кручении 
(4)
Величина 
называется жесткостью при кручении.
Подставим (4) в (3) и получим закон распределения касатель-
ных напряжений 
(5)
Как мы выяснили ранее, закон распределения напряжений линейных и наибольшие касательные напряжения возникают на контуре сечения при 
(6)
Где 
полярный момент сопротивления.
Выразим 
и 
через диаметр
Само собой, что закон распределения касательных напряжений осесимметричный и по каждому из радиусов напряжения распределяются одинаково.
Формула (6) дает возможность рассчитывать на прочность стержни, работающие на кручение, которые называют валами.
Условия прочности при кручении выглядит: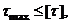 
где [ 
-допускаемое напряжение на кручение.
Может стоять задача определения коэффициента запаса по текучести. Тогда 
, где 
предел текучести при кручении.
Определение перемещений при кручении. Расчет на жесткость.
При кручении возникают угловые перемещения.
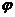- угол взаимного поворота сечений, т.е. угол на который повернутся два каких-либо сечения друг относительно друга. Пусть у стержня одно сечение заделано, а на конце приложен момент. Очевидно, что крутящий момент по длине меняться не будет 
|
|
|
На основании (4) имеем 
(7)
Если, как это имеет место в нашем случае, 
то 
(8) Угол закручивания определяем на всей длине l. Расчет на жесткость заключается в ограничении углов закручивания.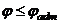 
, где 
- допускаемый угол закручивания, задаваемый обычно на длине 1м.
Расчет полых валов
Расчет полых валов производится по тем же формулам, что и
сплошных. Только выражения для 
имеют вид:
,
где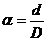 
Полый вал более эффективен при кручении, т.е. при одном и том же расходе материала он имеет большую прочность и жесткость.
ИЗГИБ
Если на стержень действуют силы перпендикулярные оси, то такое нагружение называется изгибом. Первоначально прямая ось искривляется. Мы будем рассматривать в этой лекции случай, когда силы лежат в одной плоскости. Изгиб называется чистым изгибом, если в поперечных сечениях возникает лишь один внутренний силовой фактор – изгибающий момент.
Если помимо изгибающих моментов возникают еще и поперечные силы, то изгиб называется поперечным.
Стержень. Работающий на изгиб называется балками.
Дата добавления: 2018-02-15; просмотров: 1812; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!