Преобразование моментов инерции при параллельном переносе осей.
Пусть 
- центральные оси для данной фигуры, а
и 
- произвольные оси параллельные осям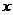 
и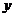 
.
Найдем моменты инерции для осей и , через, как выражаются, “старые” моменты инерции относительно осе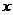й и .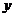
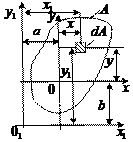Связь между “новыми” и “старыми” координатами произвольной элементарной площадки будут выглядеть
где 
и 
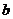- координаты старого центра в новых осях. Подставляя эти выражения в формулы для моментов инерции, и учитывая, что оси - центральные получаем:
Проделывая аналогичные выкладки и для других моментов, получаем следующий закон преобразования моментов:
; 
; 
Первыми двум выражениям можно придать словесную формулировку: момент инерции относительно какой-либо оси равняется моменту относительно оси центральной параллельной данной плюс площадь на квадрат расстояния между осями.
Моменты инерции простейших фигур.
а) Момент инерции для прямоугольника относительно центральной оси:
б) Треугольник
Момент инерции относительно оси :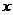 
Используя формулу преобразования момента инерции при параллельном переносе осей, получаем выражение для центрального момента инерции: 
в) Круг
Из соображений симметрии заключаем, что все центральные оси обладают равными моментами инерции. Поэтому 
Найдем вначале полярный момент инерции: 
или через диаметр: 
г) Кольцевое сечение. 
обозначив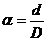 
, имеем
Преобразование моментов инерции при повороте осей.
|
|
|
Пусть х, упроизвольные площади сечения площадью F, а оси , получены из них поворотом на угол 
. Найдем моменты
инерции относительно осей , через “старые” моменты инерции
относительно осей , через “старые” моменты инерции относительно осей х, у.
Связь между координатами известна из курса аналитической геометрии
; 
.
Вычислим момент инерции 
Входящие в это выражение, интегралы представляют собой моменты инерции относительно осей 
Учитывая известные тригонометрические тождества:
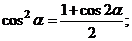
переходим к функциям угла 
.
Если проделать эту процедуру и для 
то получим следующие формулы преобразования моментов инерции при повороте
координатных осей: 
Складываем два первых уравнения, получаем 
т.е. сумма осевых моментов инерции инвариантна по отношению к повороту осей (на самом деле, она ведь равна полярному моменту инерции, а последний зависит лишь от полюса, а не от положения осей ).
Главные оси и главные моменты инерции.
Нас интересует вопрос: относительно каких осей моменты инерции принимают экстремальное значение? Из выражения (2) легко понять, что если относительно одной из осей момент принимает максимальное значение, то относительно другой момент будет минимальным.
|
|
|
Возьмем первое из выражений (1) и исследуем его на экстремум. 
Если продифференцировать второе выражение, то получим
Следовательно, условием существования экстремума будет 
. Это будет иметь место при 
Откуда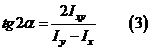 
Определение. Оси, относительно которых центробежный момент инерции равен нулю, называются главными осями. Моменты инерции относительно главных осей принимают экстремальные значения и называются главными моментами инерции.
Положение главных осей задается выражением (3). Если использовать это выражение для исключения из уравнений (1) функций угла 2, то получим формулу для определения главных моментов инерции. 
Дата добавления: 2018-02-15; просмотров: 740; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!