Схематизация геометрической формы.
КОНСПЕКТ ЛЕКЦИЙ
по
Курсу
«CОПРОТИВЛЕНИЕ МАТЕРИАЛОВ»
ОСНОВНЫЕ ПОНЯТИЯ И ДОПУЩЕНИЯ СОПРОТИВЛЕНИЯ МАТЕРИАЛОВ
Части машин и инженерных сооружений в процессе эксплуатации подвергаются воздействию сил самой различной природы. Тела, выполненные из реальных материалов, под действием сил изменяют свои размеры и форму – деформируются. При достаточно больших значениях сил конструкция может разрушиться, т.е. распасться на части, либо получить такие деформации, что ее эксплуатация станет невозможной. Проектируя конструкцию, инженер должен назначить ее размеры таким образом, чтобы гарантировать ее неразрушимость и ограничить деформации, т.е. он должен обеспечить ее прочность и жесткость, Простейшие, но вместе с тем наиболее типичные задачи подобного рода решаются в курсе “Сопротивления материалов”.
Сопротивление материалов – учебная дисциплина, занимающаяся расчетом частей машин и инженерных сооружений на прочность и жесткость. Приведенное определение является приблизительным и условным, но об этом речь впереди.
 Сопротивление материалов является частью механически твердого деформируемого тела и место данной дисциплины можно условно определить следующим образом:
Сопротивление материалов является частью механически твердого деформируемого тела и место данной дисциплины можно условно определить следующим образом:
Традиционный курс сопротивления материалов в настоящее время уже не удовлетворяет современного инженера и в курсе сопротивления материалов начинают проникать методы теории упругости, теории пластичности механики разрушения. Подобная тенденция отразится и на нашем курсе.
|
|
|
Понятие расчетной схемы конструкции.
В сопротивлении материалов анализ реального объекта (детали, конструкции) подменяется анализом расчетной схемы.
Расчетная схема – абстрактная модель реального объекта, отражающая основные характерные особенности последнего.
Схематизация осуществляется по 3 направлениям:
1. Схематизация свойств материала.
2. Схематизация геометрической формы конструкции.
3. Схематизация сил, действующих на конструкцию.
Остановимся на этом несколько подробнее.
Схематизация свойств материалов.
 а) Гипотеза сплошного однородного тела. Она состоит в том, что реальное тело, состоящее из атомов и молекул, заменяется гипотетическим сплошным однородным телом. Тело или среда называется сплошной, если любой выделенный малый объем содержит вещество. Однородность означает, что свойства тела во всех точках одинаковы. Наиболее распространенные в технике материалы – неоднородны, они имеют зачастую (напр. металлы) кристалическое строение и свойства элементов по разному выделенных из кристаллов различны. Однако размеры кристаллических зерен пренебрежимо малы по сравнению с размерами деталей, и, в результате интересующие нас тела обладают свойством относительной однородности.
а) Гипотеза сплошного однородного тела. Она состоит в том, что реальное тело, состоящее из атомов и молекул, заменяется гипотетическим сплошным однородным телом. Тело или среда называется сплошной, если любой выделенный малый объем содержит вещество. Однородность означает, что свойства тела во всех точках одинаковы. Наиболее распространенные в технике материалы – неоднородны, они имеют зачастую (напр. металлы) кристалическое строение и свойства элементов по разному выделенных из кристаллов различны. Однако размеры кристаллических зерен пренебрежимо малы по сравнению с размерами деталей, и, в результате интересующие нас тела обладают свойством относительной однородности.
|
|
|
Гипотеза сплошного однородного тела позволяет рассматривать интересующие нас величины, как непрерывные функции координат и использовать аппарат математического анализа.
б) В зависимости от поведения при нагружении различают тела упругие и пластические.
Упругие тела характеризуются однозначной зависимостью
между силами и деформациями. После снятия нагрузки деформации исчезают полностью.
У пластических тел деформации зависят не только от величины, но и от истории нагружения. После снятия нагрузки тело в первоначальное состояние не приходит. Появляются остаточные деформации.
Свойства упругости и пластичности относительны, так, например, стальная пружина, будучи сжата небольшой силой, ведет себя как упругая система, а будучи сжата большой силой, получает остаточные деформации. Это говорит о том, что для стали малые деформации упруги, а большие - пластические.
В большей части курса мы будем приписывать материалу упругие свойства.
в) В рассматриваемых нами вопросах будем считать тела изотропными, т.е. обладающими одинаковыми свойствами во всех направлениях. Тела, не обладающие таким свойством, называются анизотропными. Кристалл, например, всегда анизотропен и его анизотропия определяется расположением атомов в кристаллической решетке. Однако, технические сплавы состоят из кристаллических зерен, ориентация которых беспорядочна и произвольна, поэтому в теле, содержащем большое количество кристаллических зерен нельзя выделить какое-то предпочтительное направление. Таким образом, подобные тела можно считать изотропными.
|
|
|
В прокатанном металле зерна деформируются в направлении прокатки, и в результате материал становится анизотропен, однако подобная анизотропия обычно невелика и не учитывается в расчетах.
Существуют конструктивно анизотропные материалы (армированные пластики, фанера, железобетон).
Схематизация геометрической формы.
По принципу пространственной протяженности расчетные схемы классифицируются следующим образом:
а) Массивные конструкции – тела, у которых все три размера есть величины одного порядка (подшипники, толстостенные трубы, фундаменты под оборудование),
б) Тонкостенные конструкции: пластинки и оболочки. В этом случае два размера велики по сравнению с третьим - толщиной.
|
|
|
Подобную расчетную схему имеют сосуды для жидкостей и газов, корпуса судов и летательных аппаратов, конструкции бункеров, перекрытия и покрытия зданий, тонкостенные трубы, у которых дли-
на сопоставима с поперечными размерами, мембраны приборов и т.д.
 в) Стержни или брусья. Тела, у которых один размер – длина велик по сравнению с двумя другими размерами. Стержень характеризуется осью – некоторой кривой или прямой и поперечным сечением. Поперечное сечение перпендикулярно к оси и его центр тяжести лежит на оси.
в) Стержни или брусья. Тела, у которых один размер – длина велик по сравнению с двумя другими размерами. Стержень характеризуется осью – некоторой кривой или прямой и поперечным сечением. Поперечное сечение перпендикулярно к оси и его центр тяжести лежит на оси.
Стержни являются основным объектом изучения сопротивления материалов.
 г) Тонкостенные стержни. Тела, у которых толщина поперечного сечения значительно меньше характерного размера поперечного сечения, который в свою очередь значительно меньше длины.
г) Тонкостенные стержни. Тела, у которых толщина поперечного сечения значительно меньше характерного размера поперечного сечения, который в свою очередь значительно меньше длины.

 Подобный тип расчетной схемы имеют, например, стержни, выполненные из прокатных профилей:
Подобный тип расчетной схемы имеют, например, стержни, выполненные из прокатных профилей:
3. Силы, действующие на конструкцию.
Силы взаимодействия данного тела с другими телами называются внешними силами. Внешние силы могут проявляться при непосредственном прикосновении и на расстоянии. В первом случае они называются поверхностными силами (например, различные силы давления), во втором случае объемными или массовыми силами (сила тяжести, инерционные силы, магнитные силы и т.д.).
Под сосредоточенной силой будем понимать поверхностную силу, приложенную на участке малом по сравнению с размерами тела.
Внешние силы, приложенные к конструкции, или как еще их называют нагрузки, подразделяют на статические, прикладываемые таким образом, что ускорениями тех частей конструкции, где они действуют можно пренебречь, и динамические, когда это условие не выполняется.
Различают также нагрузки постоянные, которые неотделимы от конструкции (например, сила тяжести) и временные (нагрузки от поднимаемого груза, ветровая нагрузка и т.д.).
Внутренние силы.
Внутренние силы это силы взаимодействия между частицами тела. Связность тела в недеформированном состоянии обусловлена тем, что между его атомами существуют силы взаимодействия, и каждый атом находится под действием приложенных к нему сил. При действии внешних сил тело деформируется, меняются межатомные расстояния и взаимное расположение атомов, а, следовательно, меняются силы взаимодействия между атомами. Именно эти приращения межатомных сил (добавочные внутренние силы) представляют для нас интерес.
Однако, введя гипотезу сплошного однородного тела, мы отказались от представления об атомном строении тела и меру внутренних сил введем формальным путем.
Метод сечений.
Сплошное тело не имеет частиц. Его сплошность обуславливается внутренними связями, распределенными сплошным образом. Рассечем тело некоторой поверхности на две части. Согласно аксиоме связей, можно действие связей, нарушенных при рассекании, заменить их реакциями. Эти силы и будут внутренними силами. Из принципа отвердевания следует, что условия равновесия в данном случае будут теми же, что и для тела абсолютно твердого. Составляя уравнение статики для оставшейся части, обнаруживаем внутренние силы.
 Пусть на тело действуют система уравновешивающих друг друга сил:
Пусть на тело действуют система уравновешивающих друг друга сил:  Рассечем тело на две части и рассмотрим равновесие левой части. Тогда условия равновесия будут выглядеть
Рассечем тело на две части и рассмотрим равновесие левой части. Тогда условия равновесия будут выглядеть
1)  2)
2) 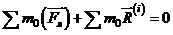
где  и
и  - соответственно главный вектор и главный
- соответственно главный вектор и главный
момент относительно некоторой точки внешних сил, приложенных к
левой части;
 - главный вектор и главный момент внутренних сил, действующих в данном сечении.
- главный вектор и главный момент внутренних сил, действующих в данном сечении.
Внутренние силы можно было бы определить из условия равновесия правой части.
Обратим внимание на то, что используя метод сечений, мы определяем некоторые интегральные характеристики (главный вектор сил, главный момент), но не устанавливаем закон распределения сил по сечению.
Внутренние силовые факторы.
Обратимся теперь к случаю стержня.
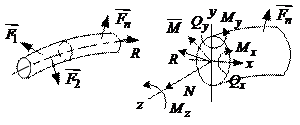 Используем метод сечений и приведем внутренние силы к центру тяжести поперечного сечения стержня. В результате приведения мы получим результирующую силу
Используем метод сечений и приведем внутренние силы к центру тяжести поперечного сечения стержня. В результате приведения мы получим результирующую силу 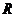 , равную главному вектору и пару сил с моментом
, равную главному вектору и пару сил с моментом 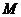 , равным главному моменту системы.
, равным главному моменту системы.
Проектируя 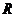 и
и 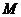 на координатные оси, получаем в общем случае 6 алгебраических величин - 6 внутренних силовых факторов:
на координатные оси, получаем в общем случае 6 алгебраических величин - 6 внутренних силовых факторов:
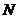 - нормальная сила;
- нормальная сила;
 и
и  - поперечные силы;
- поперечные силы;
 и
и 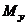 - изгибающие моменты;
- изгибающие моменты;
 - крутящий момент.
- крутящий момент.
Очевидно, что, так как внутренние силы уравновешивают внешние силы, приложенные к отсеченной части, то внутренние сило-
вые факторы можно определить следующим образом:
Нормальные и поперечные силы равняются по величине сумме проекций всех внешних сил, лежащих по одну сторону от сечения, на соответствующую ось.
Изгибающие и крутящий момент определяются как суммы мо-
ментов всех сил, расположенных по одну сторону от сечения относи-
тельно соответствующих осей.
Напряжение.
Мерой внутренних сил, величиной характеризующей интенсивность их распределения является напряжение.
 Рассмотрим тело, находящееся под действием системы уравновешенных сил.
Рассмотрим тело, находящееся под действием системы уравновешенных сил.
Будем исследовать внутренние силы в малой области, окружающей точку А. Проведем через данную точку сечение некоторой поверхностью. Внешняя нормаль этой поверхности в точке А - 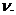 Отбросим часть, лежащую по правую сторону от сечения и заменим ее действие на оставшуюся часть внутренними силами. Выделим в окрестности точки А площадку
Отбросим часть, лежащую по правую сторону от сечения и заменим ее действие на оставшуюся часть внутренними силами. Выделим в окрестности точки А площадку  . Результирующая внутренних сил, действующих на площадке
. Результирующая внутренних сил, действующих на площадке  пусть равняется
пусть равняется  .
.
 Делим результирующую силу
Делим результирующую силу  на
на  , получаем величину среднего напряжения по площадке
, получаем величину среднего напряжения по площадке  . Величина
. Величина 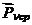 зависит от размеров площадки, перейдем к пределу, стягивая площадку к точке
зависит от размеров площадки, перейдем к пределу, стягивая площадку к точке

Величина  - называется вектором полного напряжения в данной точке по площадке с внешней нормалью
- называется вектором полного напряжения в данной точке по площадке с внешней нормалью  .
.
 Очевидно, что, выбирая другим образом ориентированную площадку, проходящую через данную точку, мы получаем другое значение вектора напряжения.
Очевидно, что, выбирая другим образом ориентированную площадку, проходящую через данную точку, мы получаем другое значение вектора напряжения.
Совокупность всех векторов полного напряжения по площадкам, проходящим через данную точку, составляет напряженное состояние в данной точке.
Величину  обычно раскладывают на две составляющие: нормальное напряжение
обычно раскладывают на две составляющие: нормальное напряжение 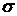 , направленное по внешней нормали к площадке и касательное напряжение
, направленное по внешней нормали к площадке и касательное напряжение 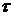 , лежащее в плоскости площадки.
, лежащее в плоскости площадки.
Перемещения и деформации.
Рассмотрим тело, имеющее такое количество связей, что движение его как жесткого тела исключено. Перемещения точек тела обусловлены деформативностью материала.
 Пусть под действием сил тело деформировалось, и точка
Пусть под действием сил тело деформировалось, и точка 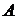 перешла в новое положение
перешла в новое положение 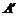 . Тогда вектор
. Тогда вектор  называется вектором перемещения, а его проекции на координатные оси обозначены соответственно
называется вектором перемещения, а его проекции на координатные оси обозначены соответственно 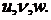
Зададим в точке 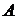 некоторое направление
некоторое направление  и пусть длина отрезка
и пусть длина отрезка  В деформированном состоянии длина отрезка изменилась и стала равной
В деформированном состоянии длина отрезка изменилась и стала равной  Тогда величину
Тогда величину
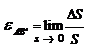 называют линейной деформацией в данной точке
называют линейной деформацией в данной точке 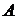 по направлению АВ. Пусть угол между отрезками ЕС и ЕD – прямой.
по направлению АВ. Пусть угол между отрезками ЕС и ЕD – прямой.
После деформации тела величина угла изменится.
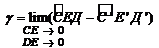 Величина называется угловой деформацией или углом сдвига.
Величина называется угловой деформацией или углом сдвига.
Уже сейчас отметим, что между напряжениями и деформациями существует связь, и эта связь принципиально может быть установлена только экспериментальным путем.
Дата добавления: 2018-02-15; просмотров: 1216; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
