Розрахунок балки-стінки методом кінцевих різниць(метод Сіток)
Розрахунок балки-стінки
Балкою-стінкою називається конструктивний елемент у вигляді балки, висота якої одного порядку з довжиною перекриваємого прольоту.
Рис. 3.11. Балка-стінка
Нехай балка-стінка має нескінченне число прольотів. Якщо виключити з розгляду крайні прольоти, то всі інші будуть перебувати в однакових умовах. У цьому випадку вісь 
, що проходить через вісь колони, є віссю симетрії. Для виконання умов симетрії функцію напружень 
варто взяти парною стосовно змінної 
, тобто у формулі) необхідно зберегти тільки члени, що містять 
|
| (а) |
Спроби задовольнити всім граничним умовам поставленої задачі за допомогою функцій напружень привели до виводу, що цієї функції недостатньо і до неї варто додати алгебраїчний поліном другого ступеня. Зберігаючи в поліномі тільки парні члени стосовно змінного , одержуємо видозмінену функцію напружень для рішення поставленої задачі:
Диференціюючи цю функцію відповідно до формул (3.10) і з огляду на те, що об'ємні сили дорівнюють нулю, знаходимо складові напружень:
| (б) |
де як і раніше 
.
Отримані формули придатні для всіх прольотів розглянутої балки-стінки, тому що від додатка до абсциси довжини функція косинуса не міняються. Отже, у відповідних точках всіх прольотів виникають однакові напруження.
|
|
|
Для визначення постійних, вхідних у формули (б), розглянемо граничні умови. Дві умови можна записати для верхньої грані. Тому що ця грань несе нормальне стискаюче навантаження інтенсивністю 
, те
при   
| (в) |
Нижня грань вільна від навантаження у всіх точках, крім тих, які лежать на осях колон. У них прикладені опорні реакції, розглянуті як зосереджені сили.
Отже, маємо ще дві умови:
при  
| (г) |
Для включення в граничні умови опорних реакцій на нижній грані розглянемо рівновагу частини балки в межах одного прольоту, відсіченою горизонтальною площиною на довільній висоті (рис. 3.12).
Рівновага частини балки
Із суми проекцій на вісь всіх сил, що діють на виділену частину балки, треба п'ята умова:
|
Нарешті, шосту умову одержуємо з розгляду вертикальних перерізів балки. По характеру зовнішніх навантажень зусилля в них зводяться до згинального моменту і поперечної сили. Оскільки поздовжня сила відсутня, сума проекцій всіх сил на вісь дорівнює нулю:
| (е) |
Підставляючи в умови (в)-(е) складових напружень (б), після інтегрування і приведення подібних членів одержуємо наступну систему рівнянь:
| (ж) |
З п'ятого рівняння (ж) знаходимо 
. З урахуванням цього результату перше рівняння приймає вид
|
|
|
Для того, щоб суми членів ряду, не залежно друг від друга, рівнялися нулю, необхідно і досить, щоб кожний член ряду рівнявся нулю. Тому
| (з) |
Аналогічно із другого рівняння (ж) одержуємо
| (и) |
а із четвертого -
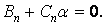
| (к) |
Відповідно до формул (і) і (к), вираз, що стоїть у фігурних дужках шостого рівняння (ж), дорівнює нулю і, отже,
Третє з рівнянь (ж) після підстановки значення 
приймає такий вид:
 
| (л) |
Для його рішення навантаження розкладемо в ряд Фур'є, використовуючи відому з математики формулу
яка дійсна при 
. Таким чином,
.
Підставляємо цей ряд у формулу (л):
звідки знаходимо 
Після цього, вирішуючи спільно систему рівнянь (з)-(к), знаходимо інші постійні:
Враховуючи, що дробі 
і 
для високих балок-стінок при висоті 
, що має порядок , близькі до одиниці, одержуємо:
; 
; 
.
Підставляючи значення знайдених постійних у формули (б), знаходимо
| (м) |
Тут гіперболічні функції замінені експонентними відповідно до залежності
Ряди у формулах (м) сходяться дуже швидко у всіх точках, за винятком тих, які перебувають поблизу нижнього краю (при малих значеннях ).
|
|
|
Результати обчислень для балки-стінки висотою 
наведені на рис. 3.13 у вигляді епюр нормальних напружень 
для двох вертикальних перерізів (на опорі і посередині прольоту) і нормальних напружень 
для двох горизонтальних перерезів.
Епюри нормальних напруг
Неважко переконатися, що ці епюри помітно відрізняються від епюр, одержуваних в опорі матеріалів.
Рамна аналогія
; 
; 
; 
; 
;
; 
; S=3K-Ш; 
.
3. Метод кінцевих різниць (метод сіток). Точне рішення бігармонічного рівняння плоскої задачі в багатьох випадках виявляється дуже складним. Для його спрощення можна застосувати наближений метод кінцевих різниць, що дозволяє замінити диференціальне рівняння системою лінійних алгебраїчних рівнянь.
Установимо залежності між похідними функції в довільній точці і значеннями самої функції в цій і в сусідніх точках. На рис. 3.3 зображена крива і показані п'ять точок, абсциси яких відрізняються на малу величину 
. По визначенню похідна функції в точці 
Крива і п'ять близько розташованих точок
Якщо інтервал між двома точками 
малий, то похідну в точці приблизно можна представити так:
| (д) |
Аналогічно можна представити похідну в точці 1:
і в точці 
:
|
|
|
Другу похідну в точці можна одержати, використовуючи двічі
подання першої похідної:
Зменшивши інтервал у два рази, можна одержати більш точне значення другої похідної в точці :
| (e) |
Далі обчислюємо третю похідну в точці :
| (ж) |
а потім і четверту:
| (з) |
У випадку плоскої задачі функція 
буде залежати від двох координат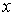 
і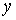 
, тому з'явиться необхідність виражати через кінцеві різниці частні похідні. Для цього досліджувану плоску область (рис. 3.4) розбивають сіткою на осередки з розмірами й 
. Для спрощення розрахунків сітку вибирають із квадратними осередками, тобто приймають 
. Частки похідні функції 
в точці можуть бути виражені через значення функції в 13 точках, пронумерованих на зазначеному рисунку.
Рис. 3.4. Розбивка досліджуваної плоскої області
Перші й другі похідні в точці по одній з координат легко скласти за аналогією з формулами (д) і (е):
| (и) |
| (к) |
Другу змішану похідну в точці знайдемо, застосувавши двічі формули (і):
| (л) |
Четверті частки похідні по одній з координат у точці складемо відповідно до формули (з):
| (м) |
а змішану похідну знайдемо, застосовуючи двічі формулу (к):
| (н) |
Зв'язок між функціями в 13 розглянутих точках установимо за допомогою бігармонічного рівняння плоскої задачі (3.11). У точці воно приймає такий вид:
Підставляючи в нього вираз четвертих похідних (м) і (н), одержуємо
| (3.19) |
Напруги в точці знайдемо за допомогою формул (3.10) без урахування об'ємних сил:
| (3.20) |
Рівняння виду (3.19) можна скласти для кожного з вузлів усередині контуру; при цьому в частину рівнянь увійдуть і значення функцій 
для вузлів на контурі і для вузлів; розташованих на відстані одного кроку поза контуром. На рис. 3.4 позаконтурна сітка показана штриховими лініями.
Значення функції на контурі й поза контуром знаходять із граничних умов. Таким чином, невідомих значень функції виявиться стільки, скільки вузлів усередині контуру, але стільки ж можна скласти і рівнянь виду (3.19). Отже, для рішення задачі рівнянь досить.
Для визначення значень функції на контурі і поза ним використовуємо ідеї проф. А. П. Сініцина, що запропонував розглядати значення функції на контурі досліджуваної області як згинальний момент у балці з таким же навантаженням, що й на даному краї області. Дійсно, якщо на верхній грані прямокутної області прикладене навантаження 
, спрямоване донизу, то для цієї грані можна скласти наступну умову:
| (о) |
Порівнюючи ії із залежністю між згинальним моментом і інтенсивністю розподіленого навантаження при згинанні балок
заключаємо, що функцію напружень на контурі пластинки можна прийняти за значення згинального моменту в даній точці балки з таким же навантаженням. При цьому балка може мати будь-яке закріплення, тому що його характер впливає тільки на значення постійних, що з'являються після інтегрування співвідношення (о):
| (п) |
На напруження вид закріплення балки впливу не зробить, оскільки напруження дорівнюють другим похідним функції і постійні 
, 
у їх вирази не ввійдуть. На нижній грані пластинки функцію варто брати рівною значенню згинального моменту зі зворотним знаком.
Похідні функції на верхній і нижній гранях 
, а на бічних — 
являють собою поперечні сили у відповідних точках балки.
Похідні на верхній і нижній гранях і на бічні можна знайти з формули
Значення похідних у точках контуру можна використовувати і для визначення значень функції в точках поза контуром.
Так, для точки 
(рис. 3.4) відповідно до формули (і) можна скласти наступне співвідношення:
Звідси знаходимо значення функції в точці 
, розташованої поза контуром пластинки:
| (3.21) |
Точно так само для точки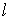 
, що лежить на бічній грані,
звідки значення функції в точки 
, що лежить поза контуром пластинки,
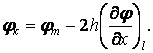
| (3.22) |
Таким чином, плоска задача зведена до відшукання значень функції у всіх вузлах сітки. Для цього, як відзначалося вище, маємо стільки рівнянь виду (3.19), скільки вузлів усередині пластинки. Значення функції на контурі пластинки знаходимо із граничних умов за допомогою співвідношень (п), а поза контуром — за допомогою співвідношень (3.21) і (3.22). Вирішуючи систему рівнянь виду (3.19), знаходимо значення функції , а за допомогою рівнянь (3.20) визначаємо напруження у всіх вузлах сітки.
Метод кінцевих різниць виявляється особливо ефективним при використанні комп'ютерної техніки. Цей метод вимагає багаторазового циклічного повторення розрахунку по тим самим формулах для кожного інтервалу. Він зводить рішення до виконання найпростіших арифметичних дій.
Система лінійних алгебраїчних рівнянь типу (3.19) добре піддається програмуванню. Зі збільшенням частоти сітки підвищується точність розрахунку.
Застосування методу кінцевих різниць особливо ефективно при розрахунку складних пластинок, коли контур непрямокутний, коли пластинка має отвори і т.д.
Дата добавления: 2018-02-15; просмотров: 658; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!