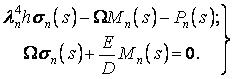Розвязок плоскої задачі теорії пружності в поліномах
В більшості випадків розв’язок плоскої задачі зводиться до знаходження функції напружень (функції Ері), яка підкоряється бігармонічному рівнянню:
і задовольняє граничним умовам на контурі диску
qx= σxx ∙nx + τxx∙ny
qy = τyx∙nx+ σyy∙ny,
де qx,qy– складові зовнішньго навантаження в точці контуру
nx ,ny - напрямні косинуси зовнішньої нормалі в даній точці контуру.
Напруження визначаються через функцію Ері такими співвідношеннями :
Під час розв’язку плоскої задачі функцію напружень часто задано, поряд з іншими виразами вона може бути у вигляді полінома.Таким чином, поліном 2,3,4,5 ступеня є бігармонічною функцією й може бути застосований до рішення плоскої задачі.За допомогою алгебраїчних поліномів можна вирішити, ряд простих задач: задача про чистий згин балки, згинанні балки на двох опорах під дією рівномірно розподіленого навантаження тощо.
Плоска задача теорії пружності в полярних координатах.
При рішенні плоскої задачі зустрічаються тіла, обмежені поверхнями кругового циліндра і радіально розбіжними площинами. У цих випадках перехід від декартовой системи координат до полярної значно спpощує рішення.
Виріжемо із пластинки товщиною, рівною одиниці, елемент 
(рис. 4.1). Для цього проведемо радіус 
під довільним кутом 
до початкового радіус-вектору, потім дамо куту нескінченно мале збільшення 
й проведемо радіус 
. Довільним радіусом 
проведемо дугу 
, потім дамо радіусу 
збільшення 
й проведемо другу дугу — 
. Сторони отриманого елемента мають наступні розміри:
|
|
|
, 
, 
.
Основні рівняння :
диференціальні рівняння рівноваги
Особливістю цих рівнянь у порівнянні з умовами рівноваги для плоскої задачі в декартових координатах є наявність у знаменнику величини
рівняння нерозривності деформацій:
Розгорнуте рівняння нерозривності деформацій:
Рівняння коші:
Формули закону Гука для узагальненого плоского напруженого стану в полярних координатах зберігають такий же вид, як і в декартовій системі
10. Осесиметрична плоска задача. Розрахунок тонкостінних циліндрів.
Зупинимося на плоских задачах, у яких напруження, а, отже, і функція  не залежать від полярного кута . У цьому випадку бігармонічне рівняння (4.26) приймає більш простий вид:
 ,
або після диференціювання
Також спрощуються вираз напружень (4.24):
При відсутності об'ємних сил залишиться тільки одне з рівнянь рівноваги (4.1)
Спростяться й геометричні співвідношення Коші (4.4), тому що складова переміщення v в силу симетрії дорівнює нулю:
З формул закону Гука (4.5) залишаться лише дві:
Осесимметричну задачу в переміщеннях можна вирішити в загальному виді. З формул закону Гука (а) знаходимо
За допомогою співвідношень (4.30) виключаємо із цих рівнянь складові деформації: Підставляючи ці напруження в рівняння рівноваги (4.29), одержуємо диференціальне рівняння відносно складового переміщення
Воно має змінні коефіцієнти. Для рішення приведемо його до рівняння з постійними коефіцієнтами за допомогою наступної підстановки:
або
Диференціюючи вираз (4.32) по змінній
Встановимо зв'язок між похідними функції З урахуванням рівності (г) одержуємо
Друга похідна
Підставляючи похідні (д) і (е) в рівняння (4.31), знаходимо Рішення цього рівняння має вигляд Вертаючись до старої змінної
Знаючи складову переміщення
а з формул (б) - складових напружень:
Постійні При розгляді довгих циліндричних оболонок з'являється можливість зневажити в поперечних перерізах згинаючим
Диференціальні рівняння рівноваги елемента циліндричної оболонки в розглянутому випадку мають такий вигляд:
Система рівнянь (7.22) шляхом виключення зусиль S, Q і
де
P — функція, що залежить від складових поверхневого навантаження й обумовлюється формулою
Крім статичних, уводяться також і геометричні гіпотези: поперечні подовження і деформації зсуву в серединній поверхні приймаються рівними нулю як величини, що мало впливають на основні зусилля оболонки:
Складові переміщення довільної точки серединної поверхні по напрямках твірної, дотичній до дуги контурної лінії й зовнішньої нормалі, позначимо відповідно Тоді складові деформації, відповідно до формул (7.10), приймуть вид
Виключимо з формул (в) переміщення. Для цього формули (в) продифференціюємо у такий спосіб:
Складаючи другу й третю формули (г), одержуємо Звідси, використовуючи п'яту формулу (г), знаходимо
Розглядаючи спільно першу й четверту формули (г) і виключая з них
Підставляючи потім похідні (д) і (е) в останню формулу (г), одержуємо диференціальне рівняння нерозривності деформацій: Використовуючи геометричні гіпотези (б), одержуємо
Диференціальне рівняння (ж) показує, що згинання елементарної поперечної смужки (деформація контуру) супроводжується розтяганням оболонки уздовж твірної (депланація поперечного переріза). Фізичні рівняння теорії оболонок можна представити в спрощеній формі, вважаючи коефіцієнт Пуассона Вносячи ці значення в рівняння (ж) і приєднуючи рівняння (а), одержуємо систему двох спільних диференціальних рівнянь
Тут напруження При з яких перші залежать тільки від змінної s, а другі — від змінної x. Одна із двох функцій приблизно задається, а друга визначається з диференціальних рівнянь. В. 3. Власов запропонував задаватися функцією де l — довжина оболонки в напрямку твірної; m — довільний параметр. Це рівняння разом із граничними умовами на криволінійних краях оболонки в кожному конкретному випадку крайової задачі буде давати систему ортогональних фундаментальних функцій Якщо обидва криволінійних краї жорстко затиснені, то при де Для оболонки, у якої один край шарнірно обпертий, а іншої - жорстко затиснений, граничні умови мають вигляд при і фундаментальні функції приймають такий вид: де Подібним чином будуються фундаментальні функції і при інших граничних умовах. Фундаментальні функції, отримані зазначеним шляхом, а також їх другі похідні мають властивість ортогональності:
Для відшукання функцій змінної представляємо їх разом з функцією (7.24) у вигляді нескінченних рядів:
Помножуючи перше рівняння (7.25) на
Тут При інтегруванні системи (7.27) з'являться вісім довільних постійних. Для їх визначення використовуються граничні умови на поздовжніх краях оболонки. Число цих умов у кожній точці одного краю дорівнює чотирьом. Ці умови можуть бути статичними, геометричними і змішаними. Таким чином, задача про рівновагу довгої циліндричної оболонки при будь-яких заданих граничних умовах і при дії довільного навантаження повністю розв'язне.
 Мы поможем в написании ваших работ! |
; 
; 
.
.
; 
; 
.
:
.
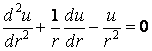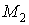, одержуємо
.
.
.
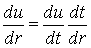
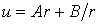, знаходимо з рівнянь (4.30) складової деформації:
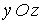й 
визначаються із граничних умов.
і крутним H моментами й поперечною силою 
. Прийнявши зазначені зусилля рівними нулю, одержимо модель оболонки, запропоновану В. 3. Власовим. Ця модель являє собою тонкостінну просторову систему, що складається з нескінченної безлічі поперечних елементарних смужок, що згинаються. Кожна смужка вподібнюється плоскому кривому стержню, що працює не тільки на розтягання або стиск, але також на поперечний згин і зсув. Взаємодія двох суміжних смужок здійснюється шляхом передачі з однієї з них на іншу тільки нормальних і зусиль, що зрушують. На рис. 7.17 ці зусилля замінені зв'язками, розташованими на рівні серединної поверхні оболонки.
приводиться до одного рівняння із двома невідомими:
— диференціальний оператор Власова четвертого порядку по змінної s, пов'язаний із законом секторіальних площ і вид, що має
, 
і 
.
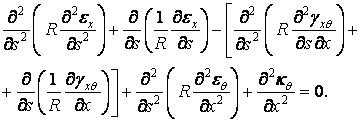
. Тоді з формул (7.11) знаходимо:
, де h – товщина оболонки.
(для кругової оболонки) рівняння (7.25) будуть мати постійні коефіцієнти. Розглянемо рішення системи варіаційним методом Бубнова-Гальоркіна у формі, розробленої для оболонок В. 3. Власовим. У цьому випадку шукані функції представляються у вигляді добутку двох функцій:
, використовуючи фундаментальні функції поперечних коливань балки, які є рішенням однорідного диференціального рівняння
, кожна з яких визначається своїм фундаментальним числом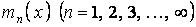 
. Так, наприклад, для оболонки, що має на криволінійних краях шарнірне обпирання, граничні умови такі: при 
і 
. Фундаментальні функції в цьому випадку чисто тригонометричні:
, і фундаментальні функції приймають вид
при 
, а друге — на 
, інтегруємо ці вирази по всій довжині оболонки. З урахуванням інтегралів (з) одержуємо систему двох звичайних диференціальних рівнянь, виражених щодо шуканих функцій 
і 
:
