Тонкі гнучкі пластини. Запис граничних умов
Тонкі пластинки звичайно розраховують по наближеній теорії — технічної теорії згинання пластинок, що заснована на наступних гіпотезах, запропонованих німецьким фізиком Г. Кирхгофом.
·Гіпотеза прямих нормалей: будь-який прямолінійний елемент, нормальний до серединної площини, залишається прямолінійним і нормальним до серединної поверхні після деформування пластинки, і довжина його не змінюється.
·Гіпотеза про недеформованність серединної площини: у серединній площині відсутні деформації розтягання, стискання і зсуву, тобто вона є нейтральною
·Гіпотеза про відсутність тиску між шарами пластинки, паралельними серединної площини. Гіпотеза дозволяє зневажати напруженням через малість у порівнянні з напруженнями σₓₓі σyy.
Жорсткими пластини вважаються якщо їх прогини не перевищують 1/5 товщини пластини.
Граничні умови для жорстих пластин:
Жорстке защімлення характеризується відсутністю прогину і кута повороту:
ω=0, ∂ω/∂x=0
Шарнірне обпирання характеризується відсутністю прогину та згинального моменту
ω=0, ∂2ω/∂x2=0
Вільний край характеризується нульовим значенням внутрішніх зусиль(згинального і крутного моментів та поперечної сили)
Mx=0,
Qzx=0
Myx=0
Ці умови можна звести до двох
Перша- 
=0
Друга 
Рівняння ососиметричного згину кільцевих пластин. Запис граничних умов.
Задача про вигин круглої пластинки буде осесиметричною, якщо навантаження на пластинку, а також умови закріплення її країв не залежать від полярного кута 
. У цьому випадку прогини пластинки також не залежать від полярного кута , а є функцією лише координати r, тобто 
.Тоді рівняння спрощується:
|
|
|
(1)
Формули згинальних моментів приймають вигляд:
Mzθ= 0;
Спрощуються й вирази поперечних сил:
Рівняння (1) можна вирішити в загальному виді. Як відомо, загальний розв’язок неоднорідного диференціального рівняння складається із суми загального розв’язку відповідного однорідного рівняння 
і якого-небудь частинного розв’язку неоднорідного рівняння 
, тобто 
Загальний розв’язок однорідного рівняння 
записується так: 
Нехай навантаження рівномірно розподілене по всій поверхні пластинки, тобто 
, тоді:
Отже, загальний розв’язок неоднорідного диференціального рівняння при рівномірно розподіленому навантаженні такий:
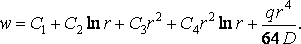
Граничні умови:
Жорстке закріплення : w = 0, φ =0
Шарнірне обпирання : w = 0, M = 0
Вільний край: М= 0 , Q =0
Рівняння осесиметричного згину круглих пластин,запис граничних умов.
Основні рівняння вигину круглої пластинки
Для розв’язання задачі про вигин круглої пластинки всі рівняння вигину пластинки, виведені в декартовій системі координат, перетворимо до полярної системи. У цьому випадку прогин пластинки й навантаження є функціями змінних r і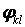 
, тобто 
й 
. Тоді відповідно до залежностей (4.3) основне рівняння вигину пластинки (5.15) приймає вигляд
|
|
|
| (5.22) |
Згинальні моменти в круглій пластинці будемо позначати так: 
— згинальний момент у перетині, перпендикулярному радіус-вектору r у розглянутій точці (радіальний згинальний момент); 
— те ж у перетині, що збігається з радіус-вектором (тангенціальний згинальний момент
Заміняючи у формулах (5.8) похідні функції прогинів по x і y на похідні по r і 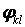, одержуємо формули згинальних моментів у полярній системі координат:
| (5.23) |
Аналогічно перетворимо формулу крутного моменту (5.10):
| (5.24) |
Поперечні сили позначимо в такий спосіб: 
— поперечна сила на площадці з нормаллю r (радіальна поперечна сила); 
— те ж, на площадці, що збігається з радіус-вектором r (тангенціальна поперечна сила). Заміняючи у формулах (5.19) похідні одержуємо вирази поперечних сил у полярній системі координат:
| (а) |
або
| (5.25) |
Позначимо 
інтенсивність наведеної поперечної сили на гранях контуру, перпендикулярних радіус-вектору r, a 
— на гранях, що збігаються з радіус-вектором. Тоді з формул (5.17) і (5.18) після заміни змінних x і y на r і 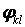можна одержати вирази наведеної поперечної сили на контурі, що враховує наявність крутного моменту:
|
|
|
Підставляючи сюди значення поперечних сил (а) і крутного моменту (5.24), знаходимо
| (5.26) |
Формули (5.22)-(5.26) являють собою основні рівняння вигину пластинок у полярній системі координат. Рівняння (5.22) служить для визначення функції прогинів серединної площини пластинки, а інші - для складання граничних умов і визначення зусиль.
22. Тонкі жорсткі пластини, циліндричний згин пластин.
Пластинкою називається призматичне або циліндричне тіло, висота якого мала в порівнянні з розмірами в плані (рис. 5.1). Висота називається товщиною пластинки й позначається 
.Площина, що ділить пластинку навпіл по товщині, називається серединної. При згинанні пластинки серединна площина перетворюється у вигнуту поверхню. Лінія перетинання бічної поверхні пластинки із серединною площиною називається контуром пластинки.Розміри і форма серединної поверхні в жорсткій пластині не змінюються.
Циліндричним вигином називається такий вигин пластин, при якому серединна площина переходить у циліндричну поверхню. На рис. 12.1 зображена пластина, затиснена одним краєм і навантажена силоміць P, рівномірно розподіленої по протилежному краю. Штриховою лінією показана форма пластини в деформованому стані (строго говорячи, біля бічних сторін поверхня не буде точно циліндричною).
|
|
|
Ри. 12.1. Циліндричний згин пластини
Відзначимо деякі особливості циліндричного згину. По-перше, у цьому випадку немає істотної різниці між вигином при малих і при великих переміщеннях, тому що скривлення серединної площини і перехід її в циліндричну поверхню відбувається без її розтягання. Виключенням є тільки той випадок, коли протилежні крайки пластини нерухомо закріплені; тоді циліндричне згинання пластини супроводжується розтяганням у поздовжньому напрямку. Помітимо що, при дуже великих прогинах навіть при найпростішій схемі закріплення (рис. 12.1) може виникнути нелінійність, пов'язана зі зміною плеча згинального моменту.
Друга особливість циліндричного згину полягає в тому, що обрис пластини в плані не грає істотної ролі, тобто при будь-якому контурі пластини розрахункові залежності ті самі.
Циліндричний згин пластин подібний до згину балок. Відмінність полягає в тому, що при згині балки поперечні деформації нічим не стиснуті, внаслідок чого форма контуру поперечного переріза спотворюється (у зоні дії напружень, що розтягують, ширина перетину зменшується, а в зоні дії стискаючих – збільшується).
При циліндричному вигині пластин поперечні деформації стиснуті за рахунок взаємодії сусідніх поздовжніх волокон. Якщо на поверхню пластини нанести поздовжні паралельні лінії (рис. 12.1), то при циліндричному вигині відстані між ними не змінюються. Це значить, що відносна деформація в поперечному напрямку дорівнює нулю.
Взаємодія поздовжніх волокон приводить до того, що в пластині виникають напруження також і в поперечному напрямку. Отже, тут має місце двохосьовий напружений стан. Систему позначення осей при вигині пластин звичайно вибирають не так, як при згині балок. Поздовжню і поперечну осі позначають х и у, а вісь, перпендикулярну серединної поверхні, — z. Відповідно нормальні напруження в довільному шарі пластини позначають 
і 
. Ці напруження показані на рис. 12.2, де зображений елемент пластини в деформованому стані.
Рис. 12.2. Напруження при циліндричному згині
Запишемо вираз відносних подовжень 
і 
в довільному шарі на відстані z від серединної площини. Тому що напружений стан у цьому випадку плоский, то
| (12.1) |
| (12.2) |
За позитивний напрямок відліку z прийнятий напрямок долілиць.
Відповідно до рівнянь (12.1), (12.2):
| (12.3) |
| (12.4) |
При малих прогинах кривизну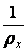 
можна замінити другою похідною згину
| (12.5) |
Тоді
| (12.6) |
Знак мінус узятий тому, що за позитивний напрямок прогину w прийнятий напрямок долілиць.
Обчислимо згинальні моменти в пластині в поздовжньому й поперечному напрямках.
Умовимося вважати моменти позитивними, якщо вони спрямовані так, як показано на рис. 12.3, тобто якщо верхні шари пластини випробовують стиск. Величини моментів будемо відносити до одиниці довжини (розмірність моментів Н·см/см). С учетом зависимостей (12.3), (12.4) и (12.5) получим
| (12.7) |
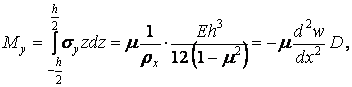
| (12.8) |
Де 
| (12.9) |
Рис. 12.. Правило знаків для моментівВеличина D називається циліндричною жорсткістю пластини.
Дата добавления: 2018-02-15; просмотров: 1258; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!