Поперечний згин вільно опертих пластин(розвязок Навє в подвійних тригонометричних рядах).
2Розглянемо шарнірно обперту по контуру прямокутну пластину під дією довільного розподіленого навантаження q(x,y) розв’язок диференціального рівняння D 
шукатимемо у вигляді нескінченного подвійного тригонометричного ряду
W(x,y)= 
(1)
Amn – постійні коефіцієнтиряду, якітребавизначити.
При шарнірному обпиранні прогини і згинальні моменти на контурі рівні нулю
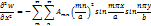
Звідси робимо висновок, що граничні умови виконуються, при х=0, х=а,та у=0, та у=b
Щоб дістати постійні коефіцієнти ряду, підставимо функцію прогину (1) в рівнянняD
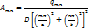
- Коефіцієнти розкладання ряду функції прогину
q=q0=const
= 
25. Поперечний згин пластин, дві протилежні сторони яких шарнірно оперті (рішення М. Леві в одинарних тригонометричних рядах).
Розв’язок Л. Нав’є, розглянутий в попередньому параграфі, придатний тільки для прямокутних пластинок, шарнірно обпертої по контуру. Більш загальним є розв’язок М. Леві. Він придатний для прямокутної пластинки, два протилежних краї якої шарнірно обперті, а два інших мають будь-яке закріплення (защемлення, шарнірне обпирання) або вільні.
У пластинки, зображеної на рис. 5.12, шарнірно обпертими є краї OC і AB.
Рис. 5.12. Пластинка із двома шарнірно обпертими краями
Граничні умови на цих краях такі:
при  й 
| (а) |
Щоб виконати ці умови, функцію прогинів можна взяти у вигляді
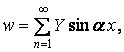
| (б) |
де Y — довільна функція одного аргументу y;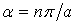 
.
|
|
|
Тому що при й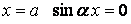 
, то функція (б) задовольняє умовам (а) відносно прогинів. Щоб перевірити умови (а) для згинальних моментів, підраховуємо другі частинні похідні функції прогинів (б) по x і y:
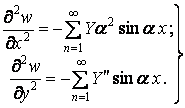
| (в) |
При й 
ці похідні, аналогічно самій функції, звертаються в нуль і, отже, умови (а) відносно згинаючих моментів також виконуються.
Функція (б) повинна задовольняти основному рівнянню вигину пластинки. Підставляючи її четверті похідні в рівняння (5.15), одержуємо
| (г) |
Для розв’язання рівняння (г) розкладемо його праву частину в тригонометричний ряд Фур'є по синусах:
| (д) |
Коефіцієнти ряду Фур'є 
є тут функцією y. Тому що розкладання виконується на відрізку 
, то їх визначають по відомій з курсу математичного аналізу формулі
| (е) |
Підставимо ряд (д) у рівняння (г):
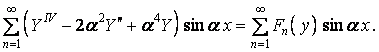
Виносячи знак підсумовування за дужки, одержуємо
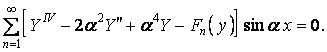
Ця умова виконується, якщо кожний член ряду дорівнює нулю:
або
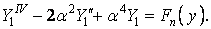
| (ж) |
Розв’язок однорідного диференціального рівняння четвертого порядку (ж) дорівнює сумі загального розв’язку відповідного однорідного рівняння і якого-небудь частинного розв’язку неоднорідного рівняння. Однорідне рівняння має вигляд
| (з) |
Його розв’язок можна представити так:
|
|
|
| (и) |
Позначивши 
частинний розв’язок рівняння (ж), одержимо його загальний розв’язок:
| (к) |
Підставляючи функцію 
у формулу (б), знаходимо
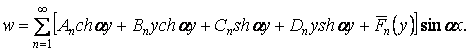
| (л) |
Функція 
є розв’язком рівняння (5.15) у випадку поперечного навантаження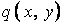 
, розподіленого на поверхні пластинки за будь-яким законом, і, як показано вище, задовольняє граничним умовам на шарнірно обпертих краях OC і AB.
Розглянемо побудову частинного розв’язку . Відповідно до правила Коші, частинний розв’язок неоднорідного диференціального рівняння четвертого порядку виражається інтегралом
| (м) |
де 
— права частина розв'язуваного рівняння, що визначається виразом (е) при заміні аргументу y на t, а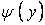 
— частинний розв’язок відповідного однорідного рівняння. Воно задовольнить умовам
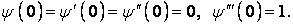
| (н) |
При розгляді однорідного рівняння (з) відповідно до формули (і) отримані чотири незалежних частинних розв’язки: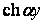 
, 
, 
, 
. З них умовам (н) задовольняє тільки наступна комбінація:
| (о) |
Замінивши у функціях (о) і (е) аргументи й підставивши ці функції у формулу (м), одержимо шуканий частинний розв’язок рівняння (ж):
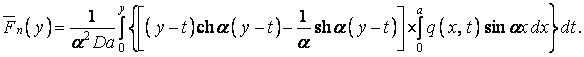
Для визначення довільних сталих 
, 
, 
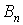і 
використовуємо граничні умови на краях OA і BC. Розглянемо пластинку, у якої ці краї жорстко затиснені (рис. 5.12). Тоді маємо наступні граничні умови:
|
|
|
при 
й 
Підставивши в них функцію прогинів (б), одержимо:
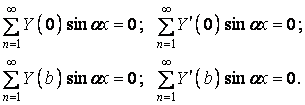
Тому що ці умови повинні виконуватися при будь-яких значеннях аргументу x, то
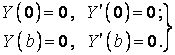
| (п) |
Вносячи в умови (п) функцію (к), одержуємо систему рівнянь для визначення сталих:
звідки
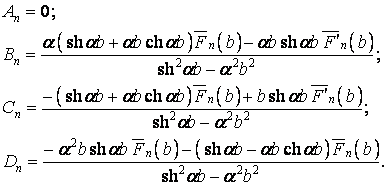
При інших закріпленнях країв OA і BC виходять інші значення сталих.
Ряди у функції прогинів і її похідних сходяться значно швидше, ніж тригонометричні ряди в розв’язку Л. Нав’є, тому розв’язок М. Леві більш зручний в практичних розрахунках навіть прямокутної пластинки, шарнірно обпертої по всьому контурі.
26. Розрахунок пластин, які працюють на згин, методом скінченних різниць (метод сіток). Запис граничних умов.
Тонкі пластинки, що мають прогини більші чверті своєї товщини, називаються гнучкими. Для них гіпотеза про недеформованість серединної площини виявляється несправедливою, тому що в ній виявляються деформації розтягання, стиску й зрушення. Крім того, зусилля серединної площини гнучкої пластинки залежать від її прогинів.
При більших прогинах точки серединної площини одержують переміщення 
й уздовж осей x і y (рис. 5.19).
|
|
|
Рис. 5.19. Переміщення в гнучкій пластинці
Тоді формули (5.4) приймають вигляд
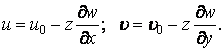
Точно так само у формулах (5.5) з'являються деформації точок серединної площини 
, 
і 
:
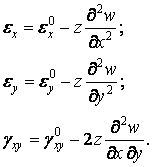
Ці формули ускладнюються ще й тим, що деформації точок серединної площини залежать від прогинів нелінійно:
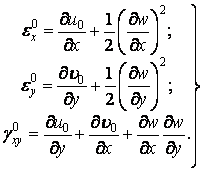
| (5.36) |
тому що в цьому випадку квадрати похідних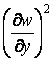 
і 
мають той же порядок малості, що й похідні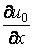 
й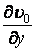 
.
Напруги в гнучкій пластинці приводяться не тільки до згинаючих і крутних моментів і поперечних сил (5.8), (5.9), (5.10), але й до нормальним і зрушуючих сил у серединній площині (рис. 5.20):
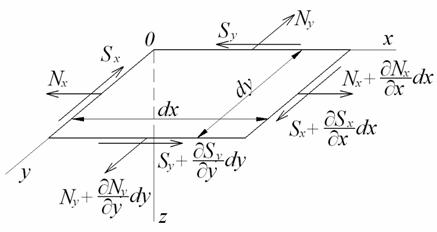
Рис. 5.20. Нормальні й зрушуючі сили
Записані формули містять невідомі складових переміщень точок серединної площини й . Крім цих переміщень, одержуємо рівняннянерозривності деформацій, що зв'язує зусилля в серединній площині пластинки:
| (а) |
Складемо рівняння рівноваги нескінченно малого елемента серединної площини гнучкої пластинки, що перебуває як під дією поперечних сил, так і під дією сил у її серединній площині (рис. 5.20). Проекція сил на вісь x дає
звідки після спрощення й розподілу на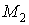 
знаходимо
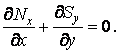
| (б) |
Аналогічно з рівняння проекцій на вісь y одержуємо
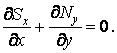
| (в) |
При проектуванні сил на вісь z гнучку пластинку варто розглядати в деформованому стані. На рис. 5.21 показаний переріз площиною, паралельною 
, нескінченно малого елемента серединної площини пластинки після скривлення. У цій площині видно сили
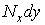і 
кути нахилу яких щодо осі відповідно рівні
і 
При проектуванні врахуємо, що косинус малого кута дорівнює одиниці, а синус - самому куту, тобто в даній площині
Рис. 5.21. Перетин елемента площиною
Спроектуємо нормальні сили в розглянутій площині на вісь z:
Після спрощення й відкидання величин третього порядку малості одержимо
| (г) |
Аналогічно можна одержати проекцію на вісь z нормальних сил у площині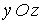 
:
| (д) |
Розташування дотичних сил після деформації гнучкої пластинки показане на рис. 5.22.
Рис. 5.22. Розташування дотичних сил після деформації
На тому же рисунку показані кути, що формуються цими силами з координатною площиною 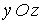. Спроектуємо ці сили на вісь z:
Після спрощення й відкидання величин третього порядку малості з урахуванням закону парності дотичних зусиль 
одержимо
| (е) |
На проекцію поперечних зусиль скривлення пластинки не впливає, тому беремо її у формі (5.12). Додаючи до цієї залежності проекції (г)—(е), розділені на 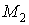, після відповідного згрупування одержуємо
Вирази, що знаходяться в дужках, відповідно до співвідношень (б) рівні (в) нулю. Підставляючи потім з (5.9) вирази поперечних сил, знаходимо
| (ж) |
Якщо ввести функцію Ері 
у формі
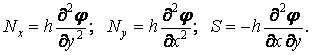
| (5.37) |
то рівняння (ж) і (а) приймуть вигляд
| (5.38) |
Тут введений оператор
| (5.39) |
При цьому оператор 
виходить із оператора (5.39) заміною функції 
на функцію .
Система нелінійних рівнянь (5.38), що зв'язує функцію напруг у серединній площині пластинки й функцію прогинів, введена німецьким ученим Т. Карманом. Разом із граничними умовами вона представляє основну систему нелінійних диференціальних рівнянь теорії гнучких пластинок. Розв’язок цієї системи в загальному вигляді не отримано. У цей час за допомогою теорії пластинок отриманий ряд частинних розв’язків для рівномірнорозподіленого поперечного навантаження, а також для пластинок, що втрачають стійкість при стиску й зрушенні в їхній серединній площині.
У випадку жорсткої пластинки, коли прогини малі в порівнянні з її товщиною, необхідно прийняти функцію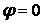 
. Тоді рівняння (5.38) зводиться до рівняння (5.16).
27. Варіаційні методи розрахунку пластин на згин.
Дата добавления: 2018-02-15; просмотров: 752; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!