Сутність варіаційних методів розв’язання
Більшість задач теорії пружності зводиться до диференціальних рівнянь із заданими граничними умовами. Точного розв’язку багатьох важливих для практики задач дотепер не отримано, тому що інтегрування диференціальних рівнянь, до яких вони зводяться, викликає значні математичні труднощі. Тому важливе значення набули варіаційні методи, що дозволяють ефективно одержувати наближене розв’язки диференціальних рівнянь із точністю, достатньої для інженерних розрахунків.
Сутність варіаційних методів полягає в тому, що функцію, що задовольняє диференціальному рівнянню при заданих граничних умовах, заміняють наближеним аналітичним виразом, що підбирається так, щоб воно щонайкраще апроксимувало цю функцію.
У теорії вигину пластинок такий підхід дозволяє звести інтегрування основного диференціального рівняння в частинних похідних до розв’язання системи лінійних алгебраїчних рівнянь або до розв’язання звичайного диференціального рівняння.
Для приведення основного диференціального рівняння вигину пластинки до системи лінійних алгебраїчних рівнянь наближене значення функції прогинів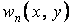 
можна вибирати у вигляді ряду з кінцевим числом членів:
| (6.1) |
де 
— лінійно незалежні функції, що задовольняють граничним умовам задачі; 
— постійні параметри, що підлягають визначенню.
Залежно від числа членів ряду (6.1) розв’язку може бути отримана з будь-яким ступенем точності. Параметри вибирають так, щоб ряд по можливості точніше відображав шукану функцію 
.
|
|
|
З різноманітних варіаційних методів розглянемо два: методи Рітца-Тимошенко й метод Бубнова-Гальоркіна.
Метод Бубнова-Гальоркіна
Метод Бубнова—Гальоркіна заснований на властивості ортогональності функцій. У курсі математичного аналізу дається наступне визначення ортогональних функцій: якщо є сімейство безперервних функцій
(а
і інтеграл добутку будь-яких двох різних функцій цього сімейства в проміжку 
дорівнює нулю:
| (6.6) |
ці функції (а) утворять у цьому проміжку ортогональну систему. Наприклад, сімейство тригонометричних функцій
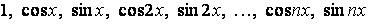
| (б) |
є ортогональною системою в проміжку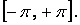 
Дійсно,
| (в) |
причому, ці інтеграли вичерпують усілякі варіанти комбінування двох різних функцій сімейства (б).
На підставі леми з курсу математичного аналізу слідує: якщо одна з функцій тотожно дорівнює нулю, наприклад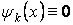 
, то вона ортогональна до всіх без винятку функцій, тому що в цьому випадку виконується умова (6.6). Як приклад можна привести функцію
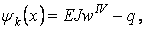
| (г) |
яка представляє собою ліву частину диференціального рівняння вигнутої осі балки. Ця функція тотожно рівна нулю при будь-яких значеннях x, і, відповідно,
|
|
|
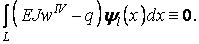
Тут інтеграл береться по всій довжині балки L, і тому функція (г) ортогональна в проміжку 
до будь-якої функції.
Якщо функцію прогинів замінити її наближеним виразом у формі ряду
| (д) |
то функція (г) уже не буде тотожно дорівнює нулю, а виходить, і не буде ортогональна в зазначеному проміжку до будь-якої функції. Можна, однак, зажадати, щоб вона була ортогональна хоча б до обмеженого класу функцій, наприклад функцій 
, що становлять ряд (д), тобто щоб
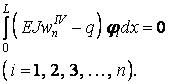
| (е) |
У результаті одержимо n лінійних рівнянь для визначення n постійних коефіцієнтів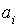 
, що входять у ряд (д).
На використанні системи рівнянь (е) для визначення значень параметрів 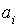і заснований метод Бубнова-Гальоркіна. Всі міркування, наведені для функції одного аргументу, можна застосувати й до функцій двох аргументів і більше. Для розв’язання задач про вигин пластинок рівняння Бубнова-Гальоркіна (е) можна представити у вигляді
| (6.7) |
де замість лінійного проміжку розглядається плоска область s, обмежена контуром пластинки, а функція 
виражається наступним подвійним рядом по області s:
| (ж) |
Таким чином, наближена функція в рівняннях (6.7), що представляє собою ліву частину диференціального рівняння вигнутої серединної поверхні пластинки (5.16), ортогональна в області s до всіх функцій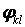 
ряду (ж), що входить у цю наближену функцію.
|
|
|
Методу Бубнова-Гальоркіна можна дати й інше, тлумачення. Функція 
являє собою проекцію на вісь z всіх зовнішніх і внутрішніх сил, що діють на нескінченно малий елемент пластинки. Функція прогинів є переміщення в напрямку тої ж осі. Виходить, функції 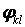теж є переміщеннями в напрямку осі z і їх можна вважати можливими переміщеннями. Отже, рівняння Бубнова-Гальоркіна (6.7) приблизно виражають рівність нулю роботи всіх зовнішніх і внутрішніх сил у пластинці на можливих переміщеннях 
.
Таким чином, метод Бубнова-Гальоркіна, як і метод Рітца-Тимошенко, виходить із принципу можливих переміщень, обидва методи рівноправні. В обох випадках апроксимуючу функцію необхідно вибирати так, щоб вона задовольняла геометричним граничним умовам. Виконання статичних умов не обов'язково.
Дата добавления: 2018-02-15; просмотров: 811; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!