Розрахунок нескінченного клина на дію зосередженої сили.
Початок системи координат вибираємо на вістрі клина. Клин обмежується двома гранями, які повернуті відносно осі х на кути α1 і α2. Довільна точка клина має координати r і γ, де α1≤ γ ≤α1.
Кут між лінією дії сили і віссю х позначаємо β. Кути β, γ, α1 і а2- додатні, якщо відраховуються від осі х протиходугодинникової стрілки .
Функція напружень для даної задачі має вигляд:
Вона задовольняє рівнянню 
і граничним умовам 
В відповідності до виразів: напруження дор.: 
Такий напружений стан наз. Простим радіальним. Але одержана формула для визначення радіальних напружень досить громіздка, тому в більшості випадків доцільно користуватися частинними випадками.
а) Сила діє вздовж бісектриси кута.
В полярній системі координат: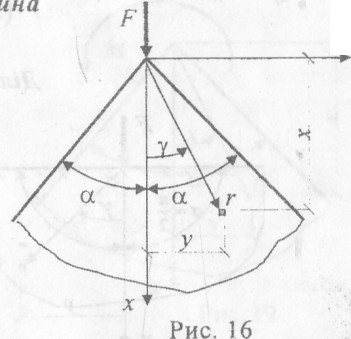 
В декартовій системі координат:
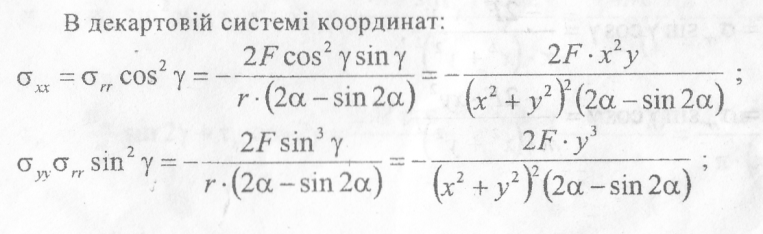
Розрахунок нескінченного клина на дію зосередженого моменту
Рішення плоскої задачі в полярних координатах у напруженнях полягає у відшуканні трьох функцій 
і 
, за допомогою трьох рівнянь: двох рівнянь рівноваги (4.1) і рівняння нерозривності деформацій (4.3) при обов'язковому задоволенні умов на поверхні.
Аналогічно тому, як було зроблено при рішенні плоскої задачі в декартових координатах, рішення в полярних координатах можна звести до відшукання однієї функції напружень 
. Виберемо цю функцію так, щоб напруження виражалися через неї в такий спосіб:
|
|
|
| (4.24) |
Підставляючи ці вирази в рівняння рівноваги (4.1), переконуємося, що при відсутності об'ємних сил останні обертаються в тотожності. Щоб перетворити рівняння нерозривності деформацій (4.3), складемо почленно формули для нормальних напружень (4.24)
.
Права частина цієї суми представлена оператором Лапласа над функцією . Отже,
і з рівняння (4.3) одержуємо
,або 
(4.25)
У розгорнутому виді рівняння нерозривності деформацій (4.25) записується в такий спосіб:
| (4.26) |
Таким чином, функція напружень для плоскої задачі в полярних координатах також повинна бути бігармонічною.
Приймаємо якусь функцію ϕ:
Приймаємо,що дана функція задовольняє граничним умовам і бігармонічному рівнянню.
Запишемо оператор Лапласа в полярній системі координат:
Вирази для напружень в полярній системі координат:
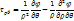
Підставивши функцію і знайшовши похідні,ми отримаємо:
Граничні умови: 
; 
Підставляємо граничні умови у 
і виражаємо значення А:
=0
Тоді,в кінцевому випадку отримаємо:
Розглянемо клин довжиною 
та знайдемо момент відносно точки О:
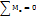
dT=dS = 
d 
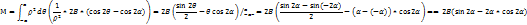
Звідси виражаємо В:
Тоді ,підставивши,значення А і В отримаємо:
13. Розрахунок пологих оболонок (оболонок малого підйому f/amin≤1/5)
|
|
|
Пологою називається оболонка, у якої стріла підйому не перевищує найменшого лінійного розміру в плані.
Теорія пологих оболонок створена В. 3. Власовим і ґрунтується на наступних гіпотезах, що доповнюють основні:
1. Оболонка приймається настільки пологої, що геометрію її поверхні можна приблизно вважати співпадаючою з геометрією площини її проекції. Це значить, що для квадрата лінійного елемента пологої оболонки із прямокутним планом замість виразу
можна прийняти
тобтовважати, що 
, а координати 
й 
рівні відповідно x і y. Це означає також, що у вихідних рівняннях гауссова кривизна
2. У рівняннях рівноваги можна відкинути члени, що містять поперечні сили.
3. У виразах для згинальних деформацій досить зберегти тільки члени, що містять переміщення в напрямку нормалі до серединної поверхні оболонки.На риспоказані зусилля, що діють на нескінченно малий елемент серединної поверхні пологої оболонки із прямокутним планом.
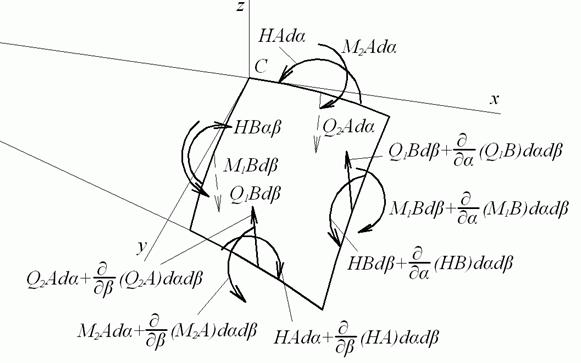
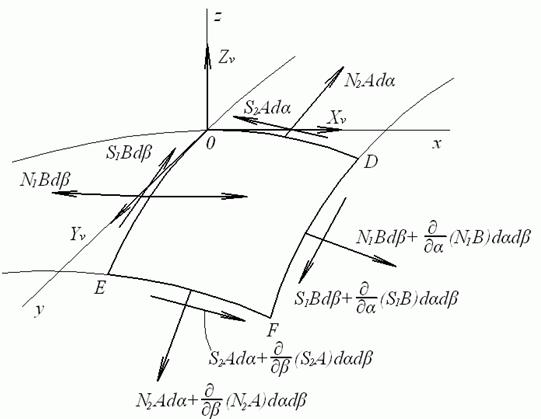
Розглядаючи обидва рисунки спільно і з огляду на прийняті гіпотези, одержимо наступні рівняння рівноваги:
| (7.42) |
Вивод геометричних рівнянь можна проробити аналогічно тому, як це зроблено для циліндричної оболонки. З урахуванням прийнятої гіпотези геометричні рівняння виходять у такій формі:
|
|
|
| (7.43) |
Фізичні рівняння:
| (7.44) |
Система рівнянь (7.42)—(7.44) може бути зведена до двох розв'язних рівнянь із двома невідомими функціями w і 
. Функція напружень уводиться аналогічно тому, як це робилося в плоскій задачі теорії пружності. Зусилля безмоментного напруженого стану виражаються через функцію в такий спосіб:
| (7.45) |
У практичних задачах поверхневе навантаження найчастіше нормальне до серединної поверхні оболонки. Обмежуючись тільктакимизадачами,приймемо: 
. У цьому випадку зусилля 
, 
, S у формулі (7.45) тотожно задовольняють першим двом рівнянням рівноваги (7.42), а третє рівняння після підстановки в нього зусиль (7.44) і деформацій з формул (7,43) здобуває вид
| (а) |
де оператори позначають:
| (7.46) |
Для виводу другого розв'язного рівняння виключимо з перших трьох співвідношень (7.43) складового переміщення, як це робилося при виводі рівнянь нерозривності деформацій. У результаті одержимо
Замінивши в цьому рівнянні деформації зусиллями за допомогою формул (7.44), а потім зусилля функцією напружень за допомогою формул (7.45), знайдемо
|
|
|
| (б) |
Таким чином, одержуємо основну систему рівнянь (а) і (б) теорії пологих оболонок:
| (7.47) |
Ці рівняння справедливі для оболонок, що мають постійні кривизни 
й 
, і для оболонок, серединна поверхня яких утворена переміщенням плоскої кривої по довільній напрямні зі збереженням паралельності цій кривій її первісному положенню (оболонки переносу).
Система диференціальних рівнянь (7.47) узагальнює дві задачі теорії пружності: плоску задачу і задачу про згинання пластинки. Дійсно, вважаючи головні кривизни оболонки рівними нулю, одержуємо 
, а система розпадається на два незалежних рівняння:
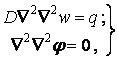
перше з яких являє собою рівняння Софи Жермен для згинання пластинки, а друге - бігармонічне рівняння плоскої задачі теорії пружності.
Рішення системи (7.47) представляє більші труднощі, доцільно застосовувати варіаційні методи рішення: Бубнова-Гальоркіна або метод Рітца-Тимошенко.
Дата добавления: 2018-02-15; просмотров: 629; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!