Основні рівняння теорії пружності. Розвязання задачі теорії пружності в напружності(р-ня Бельтрамі-Мічела).
Рішення задачі теорії пружності в напруженнях при постійних об'ємних силах
Обмежимося випадками, коли об'ємні сили постійні по всьому обсягу тіла або дорівнюють нулю. Це обмеження дозволяє значно спростити деякі рівняння прирішенні задач в напруженнях, так як всі похідні складових об'ємних сил по координатах 
обертаються в нуль.
Розглянемо властивості функцій 
і 
при постійності об'ємних сил. Продифференціював перше рівняння Ламе (2.9) по 
друге — по 
третє — по 
й почленно склавши, одержимо
| (2.13) |
Вираз, що знаходиться в перших дужках, являє собою оператор Лапласа над функцією :
Вираз в других дужках можна перетворити, і виявляється, що це той же оператор Лапласа над функцією :
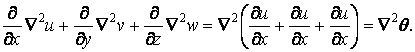
Тоді замість (2.13) одержимо
або
| (2.14) |
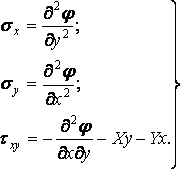Функція, що підкоряється рівнянню (2.14), називається гармонійною. Отже, при постійності об'ємних сил об'ємна деформація 9 є гармонійна функція.
Підставляючи в рівняння (2.14) вираз об'ємної деформації (1.65) і ділячи на постійний множник, одержуємо
| (2.15) |
тобто при постійності об'ємних сил перший інваріант напруженого стану теж є функція гармонійна.
При рішенні задачі теорії пружності в напругах за основні невідомі приймають, як уже говорилося, шість складових напружень 
Для їх визначення трьох рівнянь рівноваги (2.1) недостатньо й тому потрібно додати ще шість рівнянь нерозривності деформацій (2.4). В останні входять складові деформації, які необхідно попередньо виразити через напруження. Підставляючи в перше рівняння (2.4) вираз деформацій (2.5), одержимо
|
|
|
| (2.16) |
Для практичного застосування рівняння (2.16) варто перетворити, виключивши з нього дотичне напруження 
. Для цього продифференціюєм перше рівняння рівноваги (2.1) по х, друге — по у, третє — по z. Складаючи почленно два перших з отриманих рівнянь і віднімаючи третє, знаходимо
| (2.17) |
Підставляючи (2.17) у рівняння (2.16), одержуємо
Додамо і віднімемо в цьому рівнянні 
Тоді з урахуванням рівняння (2.15)
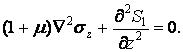
Аналогічно можна перетворити інші рівняння нерозривності деформацій (2.4). В результаті одержимо шість рівнянь:
| (2.18) |
Ці рівняння одержав італійський математик Е. Бельтрамі. Трохи пізніше австралієць Дж. Мичелл вивів аналогічні рівняння для загального випадку, коли об'ємні сили не постійні і,отже, у праву частину рівнянь замість нулів входять члени, що містять похідні від об'ємних сил. Тому рівняння (2.18) називають рівняннями Бельтрамі-Мичелла.
Таким чином, для рішення завдання теорії пружності в напруженнях доводиться інтегрувати дев'ять рівнянь (2.1) і (2.18). Наявність трьох зайвих рівнянь необхідно для одержання однозначного рішення, про що вже говорилося при виводі рівнянь нерозривності деформацій (2.4), наслідком яких є рівняння Бельтрамі-Мичелла.
|
|
|
Отримані після інтегрування шість складових напружень повинні задовольняти умовам на поверхні (2.2). Після цього по формулах закону Гука (2.5) визначають складові деформацій, а з геометричних співвідношень Коші (2.3) - складових переміщень.
Дата добавления: 2018-02-15; просмотров: 522; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!