Оптимізаційні моделі управління. Сглажування в задачах оптимізації фонду споживання
Один из методов позволяющих усилить прикладное значение в моделях минимизации фонда потребления заключается в введении условия обеспечения min уровня потребления, которое не должно быть меньшим некоторой введенной величины  . С учетом этого наша задача запишется следующим образом:
. С учетом этого наша задача запишется следующим образом:

(dy)/(dt)=(1/B)*u

Y(0)=y0
при задании  необходимо помнить, что она должна быть не больше y0, т.к. уничтожено вариант развития.
необходимо помнить, что она должна быть не больше y0, т.к. уничтожено вариант развития.
Функция Гамильтона:

Сопряженная система уравнений:

.условие трансверсальности:

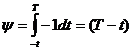


Два варианта:
1) 
T-t>-B
т.е. Н достигает максимального значения при 
2) T>t-B
u*=0
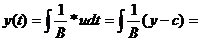









Недостаток такого подхода заключается в том, что на участке (Т-В) до Т мы имеем постоянный НД и потребление в пересчете на душу населения в предположении что численность населения растет, НД и потребление на душу населения снижается.
Оптимізація моделі управління. Оптимізація норми виробничого накопичення
это еще один подход к решению задачи максимизации общего фонда потребления.
При исследовании модели, норма производственного накопления предполагается постоянной на планируемый период. В этом случае динамика НД описывается моделью Фаррада-Дамара:
 (1), где
(1), где
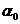 - начальная постоянная норма накопления
- начальная постоянная норма накопления
Критерий оптимальности принимает вид:
 = (2)
= (2)

Задача сводится к максимизации интеграла (2) по  .
.
Определение оптимальной нормы  означает и определение растоянного типа прироста
означает и определение растоянного типа прироста 
Результат решения задачи максимизации 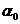 является функцией оптимальной длины планового периода Т. Следовательно и функционал полезности также является функцией от Т.
является функцией оптимальной длины планового периода Т. Следовательно и функционал полезности также является функцией от Т.
Оптимальная норма накопления обладает следующими свойствами:
При Т>2B оптимальное значение  (Т) находится в пределах:
(Т) находится в пределах: 
Следовательно, темп роста  лежит в пределах соотношения:
лежит в пределах соотношения:
 при
при 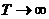
Оптимальный темп прироста НД при постоянной норме накопления также является возрастающей функцией от продолжительности планового периода.

Следовательно для оптимального темпа прироста имеет место соотношение:
 при
при 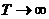
Недостатком данной модели является сильная зависимость от длины планового периода. Этот недостаток можно устранить частично рассматривая функционал дисконтирующего потребления.
В этом случае длительность периода эффективного накопления увеличивается.
В связи с оптимизацией нормы накопления возникает задача о выходе постоянную норму накопления.
Пусть экономика функционирует с некоторой нормой накопления 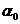 . Необходимо перейти на норму накопления
. Необходимо перейти на норму накопления  , которую поддерживать в дальнейшем.
, которую поддерживать в дальнейшем.
При этом выбирая траекторию потребления  . Считаем что
. Считаем что  , которое равнялось
, которое равнялось  и система может выдержать такой рост потребления.
и система может выдержать такой рост потребления.
К решению данной задачи можно подходить с 2-ух позиций:
1) Нахождение времени выхода на заданную норму накопления.
2) Время считается заданным и нужно определить как выйти на заданную норму потребления.
При экзогенно заданном темпе роста  задача состоит в определении времени выхода на заданную экзогенно норму накопления
задача состоит в определении времени выхода на заданную экзогенно норму накопления  , которая в дальнейшем будет поддерживаться.
, которая в дальнейшем будет поддерживаться.
Задача сводится к решению управления относительно переменной t1.

В частном случае в качестве  можно использовать
можно использовать  , т.е. оптимальную норму накопления для дальнего горизонта планирования. При этом необходимо задать период, для которого вычисляется
, т.е. оптимальную норму накопления для дальнего горизонта планирования. При этом необходимо задать период, для которого вычисляется  .
.
Однако, по мере продвижения от 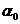 до
до  будет проходить время и для оставшегося периода
будет проходить время и для оставшегося периода  будет уже другим.
будет уже другим.
Окончательная траектория нормы производственного накопления имеет вид: при  рост нормы накопления и в дальнейшем поддержание её на уровне
рост нормы накопления и в дальнейшем поддержание её на уровне  (t*).
(t*).
Дата добавления: 2018-02-15; просмотров: 95; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
