Оптимізаційні моделі управління. Оптимізація фонду споживання
В моделях данного класса рассматривается динамика валового общественного продукта и национального дохода.
Зависимость их роста от распределения на фонд потребления, накопления в каждый момент времени и мгновенном эффекте от вложений.
Математической основой для такого рода задач является теория оптимального потребления.
Национальный доход представляется в виде суммы двух составляемых:
Y(t)=u(t)+c(t) (1)
U - накопление
С - потребление
Y - национальный доход
В основе модели лежит предположение о пропорциональности между накоплением и приростом валового общественного продукта:
U(t)=b*((dy)/(dt)) (2)
Где b – капиталоемкость валового продукта
Валовый общественный продукт связан соотношением:
X(t)=a*x(t)+y(t),
Где а – агрегированный показатель прямых материальных затрат
Отсюда X(t)=Y(t)*(1/(1-a))
Построим для національного дохода соотношение:
Y(t)=b*(1/(1-a))*dy/dt + c(t) (3), где
x(t) – общественный продукт
с(t) – потребление
b/(1-a)=B – капиталоемкость национального дохода
В простейшем случае c(t)=0, c(t)=const, uc(t) = C0*Ert
 (5)
(5)
Данного класса задача относится к задачам оптимизации управления. В общем виде она формируется в следующем виде:
Состояние системы x(t) и управления v(t) определяют скорость изменения состояний системы:
(dx(t)/dt)=x(t)=F[x(t),v(t),t]
Управление такого вида называется управлением перехода.
Переменная времени t вводится в явном виде
Зная, составление системы в начальный момент времени и выбрав управление, мы можем однозначно определить составление системы
|
|
|
Выбор управления осуществляется исходя из целей функционирования системы, которые формализованы в критерий функционал полезности 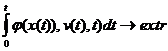 , зависящий от состояния, управления, времени.
, зависящий от состояния, управления, времени.
В задачах экономической динамики аддитивны по времени и отражает совокупный эффект функционирования системы.
Наша задача заключается в том, чтобы определить extr функционала при условии, что фазовое состояние описывается соотношением:
x(t)=F[x(t),v(t),t]
Переменные управления удовлетворяют ограничениям:
 ,
,  и задано начальное состояние системы X(0)=X0 (4)
и задано начальное состояние системы X(0)=X0 (4)
Для решения такого класса задач применяется принцип максимума Понтрягина (необходимое условие)
Задача (4) представляет собой задачу оптимального управления, которая может быть решена при помощи принципа максимума Понтрягина.
Принцип максимума Понтрягина
Если v*(t) – оптимальное управление, т.е. управление, которое максимизирует функционал полезности в задаче (4), то существует такой вектор переменных ψ(t) (его размерность равна размерности вектора состояний x(t) ), что для любого момента времени t функция Гамильтона H, зависящая от x,v, ψ,t равняется  достигает максимума на управление (v*,t)
достигает максимума на управление (v*,t)
|
|
|
т.е. max H (x,v,t, ψ) = H(x,v*,t, ψ) (6)
При этом функция ψ(t) удовлетворяет (d ψ/dt)=-du/dx
и условно трансверсальность ψ(Т)=0
Необходимо обеспечить max (Т)
Оптимизируем траекторию национального дохода, при отсутствии ограничений на потребление dy/dt=1/B (7)
В качестве управления выступает u(t), которое удовлетворяет ограничениям
0≤a(t)≤y(t) (8)
Начальное условие при t=0
Y(0)=y0 (9)
Применим принцип максимума. Функция Гамильтона примет вид:
H=Y(t)-u(t)+ ψ*(1/B)u(t)
Сопряжонная система диф уравнений будет иметь вид:
d ψ/dt=-du/dy=-1
Условие трансверсальности:
ψ(T)=0 отсюда 
H=Y-u+(T-t)*1/B*u=Y+u(((T-t)/B)-1)
Функция Не линейно зависящая от u
Рассмотрим 2 случая:
(T-t)/B-1>0
T-B>t
Тогда Н достигнет своего max при самом большом возможном управлении, т.е. u*(t)=Y(t)
В этом случае норма производственного накопления равна 1, что означает рост максимально возможным технологическим темпом.
2) t>T-B
Hе достигнет максимума при u*=0, что означает отсутствие накопления
При t<T-B мы мы установили что u*(t)=y*(t), а решение диф уравнения имеет вид:
y(0)*et/B
тогда y*(T-B)=y0*e(t-B)/B при t>T-B, u*(t)=0, y*(t)=c*(t)=y**(T-B)
Такая модель называется моделью с релитным (0;1) переключением.
Первый раз в момент t0=0 норма производственных накоплений переключается с 0 на 1. А затем в момент Т-В с 1 на 0.
|
|
|
Рассмотрение возможностей системы позволяет сделать вывод о качественных свойствах модели:
1) если речи идет о краткосрочном планировании, т.е. на участке Т-В оптимизировать распределение дохода между накоплением и потреблением с помощью данной модели не имеет смысла. Норму надо задавать экзогенно.
2) При среднем и дальнем планировании оптимальная траектория является недопустимой с экономической точки зрения, т.к. на первом этапе предполагается нулевое потребление. Создается ситуация конца света.
3) Ситуация первоначального полного накопления возникает потому что в модели предполагается, что не имеет значения когда потребляем
Чтобы устранить вводят гипотезу о существовании потребительских предпочтений.
Эффективность благ настоящего выше, чем эффективность благ будущего.
 w>0 (10)
w>0 (10)
Задача имеет тот же самый вид (7)-(9)
Применим принцип максимума Понтрягина, составим Гамильтон:
Н=E-wt*(y-u)+ ψ*(1/B)*u
Составим сопряпряжонную систему дифуров и запишим условие трансверсальности:
(d ψ/dt)=-(dH/dy)=-e-wt
Условие трансверсальности:
ψ(Т)=0


V=(-1/w)*e-wt, тогда ψ(t)=((e-wt)/w)-(1/w)e-wT

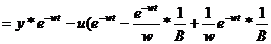
Гамильтон зависит от u
Необходимо рассмотреть два случая:
|
|
|
когда коэффициент перед u>0 и u возрастает
когда коэффициент <0
1) 
u*(t)=y*(t)


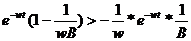




Bw может быть < 1 и > 1
Если Bw <1, то 
2. После этого момента, т.е.  u*(t)=0
u*(t)=0
Таким образом при t<T-  , то оптимальное управление u*(t)=y*(t)=y0*et/B
, то оптимальное управление u*(t)=y*(t)=y0*et/B
А при t>T-  u*(t)=0,
u*(t)=0, 
 - скорректированная капиталоемкость
- скорректированная капиталоемкость
Оптимальная траектория имеет переключение в точке t=T- 
Суммарный фонд потребления:
c*(t)=  *y**(T-
*y**(T-  )
)
Хотя момент времени t приближен к моменту времени t=0, однако на этапе все равно есть потребление.
Дата добавления: 2018-02-15; просмотров: 95; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
