Використання виробничих функцій для моделювання одно секторної економіки. Модель Солоу. Золоте правило накопичення.
Стационарный объем капитала k*g, который максимизирует потребление называется золотым уровнем накопления капитала или уровнем золотого правила.
Если мы установили раньше, что существует только один уровень потребления, то мы можем его найти из необходимого условия оптимальности.
f=c+ λk+k* так, как стационарный уровень, то k=0.
c(t)=f(t)- λk
Стационарное потребление показывает, что увеличение стационарного объёма капитала двояко влияет на величину стационарного потребления, которое возрастает за счет большего объема производства и уменьшается за счет амортизации и роста населения (μ+η).
Если k<kg то рост капитала увеличивает объёмы капитала сильнее, чем λ, α2>α1=ß
Если k>kg увеличение объема капитала уменьшает объемы потребления, прирост производства меньше прироста λ, функция более пологая, чем λ'k α3>α2=ß

Если k=k*g то α1= ß=λ при объеме капитала k=k*g линии амортизации + населения и производственная функция имеют наклон равный граничному (придельному) продукту капитала.
с*- это максимум функции f(k)- λk
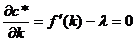 - необходимое условие.
- необходимое условие.
МРК = λ = ß = α1
Где МРК – придельный продукт капитала.
Планування випуску на рівні галузі. Лінійні моделі економіки. Принципова схема МОБ в натуральному виразі.
Планирование выпуска на уровне отрасли.
Под балансовой моделью понимают систему уравнений, увязывающих материальные, трудовые и финансовые ресурсы с целью анализа перетока продукции между отдельными экономическими объектами (отраслями, регионами, предприятиями и их подразделениями), обеспечивающего такое функционирование производственного сектора, при котором имеет место баланс между объемом выпуска продукции и совокупной (производственной и конечной потребностью в ней).
Балансовые или матричные модели применяются для анализа и планирования производства и распределения продукции на различных уровнях иерархии от предприятия до макроэкономической системы в целом.
К наиболее распространенным видам относятся:
- частичные материальные, трудовые и финансовые балансы, относящиеся к народному хозяйству страны или отдельных регионов
- модели межотраслевого баланса производства и распределения продукции (МОБ);
- матричные техпрофин планы развития отраслей, предприятий и фирм.
Принципиальная схема МОБ натуральном выражении.
Схема МОБ в натуральном выражении представляет собой синтез двух квадратов-разделов баланса (табл.1)
формирование затрат на производство в разрезе отдельных видов продукции (отраслей),
использование результатов производства в экономической системе (производственное и конечное потребление).
| Поступление произв.ресурсов | Использование результатов пр-ва | ||||||||||||||
|
|
| Произведено | Прочие ресурсы | Пр-во продукции по отраслям |
| ||||||||||
| Импорт | Невосполн Ресурсы | Запасы и резервы на начало периода | Итого | 1 | 2 | … | n | Итого | Конечное потребление | Итого | |||||
| Внутр. | Экспорт | Инвест | Валовый выпуск | ||||||||||||
| Отрасли пр-ва продукции | 1 | q1 | S1 | S1 | S1 | X1 | X11 | X21 | … | Xn1 | Y1 | X1 | |||
| 2 | q2 | S2 | S2 | S2 | X2 | X12 | X22 | … | Xn2 | Y2 | X2 | ||||
| … | … | … | … | … | … | … | … | … | … |
| |||||
| n | qn | Sn | Sn | Sn | Xn | X1n | X2n | … | Xnn | Yn | Xn | ||||
Табл. 1. Схема МОБ в натуральном выражение
Сущность МОБ отражает соотношение:
1. Xi =  i=1,n
i=1,n

Сумма мат.затрат какой-либо отрясли и её условно-чистого продукта равна валовой продукции отрасли.
2. Валовая продукція і-ой отрясли равна сумне мат.затрат потребителей продукции и конечной продукции і-ой отрясли.
3. Xi =  i=1,n
i=1,n
Просуммировав по j систему Xi =  и по i систему
и по i систему
Xi =  получим
получим


Следовательно 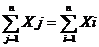
Сумма условно-чистого продукта всех отраслей равна сумме конечной продукции всех отраслей

Стоим.состав НД= Мат.состав НД
Уравнение  показывает , что в МОБ выполняется принцип единства материального и стоимостного состава НД.
показывает , что в МОБ выполняется принцип единства материального и стоимостного состава НД.
Планування випуску на рівні галузі. Лінійні моделі економіки. Принципова схема МОБ в грошовому виразі.
Планирование выпуска на уровне отрасли.
Под балансовой моделью понимают систему уравнений, увязывающих материальные, трудовые и финансовые ресурсы с елью анализа перетока продукции между отдельными экономическими объектами (отраслями, регионами, предприятиями и их подразделениями), обеспечивающего такое функционирование производственного сектора, при котором имеет место баланс между объемом выпуска продукции и совокупной (производственной и конечной потребностью в ней).
Балансовые или матричные модели применяются для анализа и планирования производства и распределения продукции на различных уровнях иерархии от предприятия до макроэкономической системы в целом.
К наиболее распространенным видам относятся:
- частичные материальные, трудовые и финансовые балансы, относящиеся к народному хозяйству страны или отдельных регионов
- модели межотраслевого баланса производства и распределения продукции (МОБ);
- матричные техпрофин планы развития отраслей, предприятий и фирм.
Принципиальная схема МОБ в денежном выражение.
Схема межотраслевого баланса в денежном выражение (табл) состоит из 4 квадратов имеющих различный экономический смысл.
| Отрасли производители | Отрасли потребители | Конечный продукт | Валовый продукт | |||||
| 1 | 2 | 3 | n-1 | n | ||||
| 1 | X11 | X12 | X13 | X1n | Y1 | X1 | ||
| 2 | X21 | X22 | X23 | X2n | Y2 | X2 | ||
| … | I | II | ||||||
| n | Xn1 | Xn2 | Xn3 | Xnn | Yn | Xn | ||
| Амортизация | C1 | C2 | C3 | Cn | Cкон | |||
| Оплата труда | V1 | V2 | V3 | III | Vn | Vкон | ||
| Чистый доход | m1 | m2 | m3 | mn | m кон | |||
| Валовый продукт | Х1 | Х2 | Х3 | Xn | 
| |||
Первый квадрат – это таблица межотраслевых потоков. Показатели, Xij – это объёмы межотраслевых потоков продукции i – номер отрасли производителя j - потребителя, - стоимость продукции произведенной в отрасли i и потреблённой в j – ой.
Сумма всех элементов квадратной матрицы n-ого порядка расположенной в квадрате I – равна годовому фонду восстановлению амортизации средств пр-ва в материальной сфере.
Второй квадрат, содержит конечную продукцию всех отраслей материального производства, где под конечной продукцией понимается продукция, выходящая из сферы производства в конечное использование (на потреблении и накопление)
В данной схеме конечный продукт свернут в один столбец. Y=(Y1…Yn)
В развернутой схеме он может быть дифференцирован по направлениям использования: личное потребление населению накопления, покрытия убытков, экспорт и т.д.
Третий квадрат – характеризует национальный доход, но со стороны стоимостного состава – как сумма «чистой продукции» и амортизации. Под чистой продукцией понимают: «оплата труда» + «чистый доход отрасли: V j + m j
Условно чистая продукция отрасли j Z j
Z j = C j + (V j + m j)
Четвертый квадрат отражает конечное распределение и использование НД.
Данные важны для определения доходов и затрат населения, источников финансирования кап. вложений, анализа доходов по группам потребителей.
Планування випуску на рівні галузі. Лінійні моделі економіки. Економіко-матиматична модель МОБ.
Планирование выпуска на уровне отрасли.
Под балансовой моделью понимают систему уравнений, увязывающих материальные, трудовые и финансовые ресурсы с елью анализа перетока продукции между отдельными экономическими объектами (отраслями, регионами, предприятиями и их подразделениями), обеспечивающего такое функционирование производственного сектора, при котором имеет место баланс между объемом выпуска продукции и совокупной (производственной и конечной потребностью в ней).
Балансовые или матричные модели применяются для анализа и планирования производства и распределения продукции на различных уровнях иерархии от предприятия до макроэкономической системы в целом.
К наиболее распространенным видам относятся:
- частичные материальные, трудовые и финансовые балансы, относящиеся к народному хозяйству страны или отдельных регионов
- модели межотраслевого баланса производства и распределения продукции (МОБ);
- матричные техпрофин планы развития отраслей, предприятий и фирм.
Экономико-математичная модель МОБ
Основой информ. Обеспечения модели МОБ и его базой является технологическая матрица, содержащая коэффициенты прямых материальных затрат на производство единицы продукции с элементами
а i j (i = 1, m , 1, n) , а i j = const.
а i j = Xij/ Xj
которая строится в предположении:
о единственности технологии и продукта для отрасли (экон. объекта)
независимости в отрасли j нормы производственных затрат промежуточной продукции отрасли i от объема выпускаемой продукции.
Коэффициенты прямых мат.затрат а i j показывает какое кол-во продукта i-ой отрасли необходимо затратить для производства единицы продукции j-ой отрасли.
Тогда, система уравнений баланса запишется в виде:
Xi =  i=1,n
i=1,n
Если ввести в рассмотрение матрицу А={ а i j } (i=1,n , j=1,n ) – матрицу коэффициентов прямых материальных затрат;
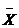 ={ х i } (i=1,n ) – вектор-столбец валовой продукции;
={ х i } (i=1,n ) – вектор-столбец валовой продукции;
 ={ Y i } (i=1,n ) – вектор-столбец конечной продукции;
={ Y i } (i=1,n ) – вектор-столбец конечной продукции;
то система уравнений Xi =  i=1,n в матричной форме будет иметь вид:
i=1,n в матричной форме будет иметь вид: 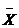 = А
= А 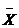 +Y
+Y
Система 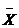 = А
= А 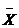 +Y носит название:
+Y носит название:
Экономико-математическая модель МОБ;
Модель Леонтьева;
Модель «Затраты-Выпуск»
И призвана ответить на вопрос:
Можно ли в условиях данной технологии удовлетворить конечный спрос.
Ответ на него сводится к существованию неотрицательного решения системы
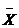 = А
= А 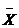 +Y , заданной квадратной несимметричной матрицей А с неотрицательными коэффициентами.
+Y , заданной квадратной несимметричной матрицей А с неотрицательными коэффициентами.
Выделяют три варианта расчета:
Определить объемы конечной продукции каждой отрасли Yi при известных выпусках валовой продукции Xi
 =
= 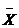 - А
- А 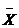 = (Е-А)
= (Е-А) 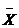 , где
, где
Е – единичная матрица порядка n.
Определить объемы валовой продукции каждой отрасли при известных объемах конечной продукции Yi
Отсюда 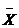 = (Е-А)-1 *
= (Е-А)-1 *  =В*Y
=В*Y
В – матрица, В={bij} i=1,n j=1,n
Для ряда отраслей известны объемы валовой продукции, а для остальных объемы конечной. Определить объемы валовой и конечной продукции для всех отраслей.
Из 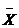 = (Е-А)-1 *
= (Е-А)-1 *  =В*Y следует, что вал.продукция представима как взвешенная сумма объемов кон.продукции:
=В*Y следует, что вал.продукция представима как взвешенная сумма объемов кон.продукции:
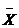 =
=  i=1,n
i=1,n
Весовые коэффициенты bij носят название коэф.полных затрат и показывают сколько всего необходимо произвести валовой продукции i-ой отрасли для выпуска в сферу конечного использования 1 единицы продукции j –ой отрасли и включают в себя как прямые, так и косвенные затраты всех порядков.
Выпуск продукции на самом деле затрагивает целый комплекс не только отраслей, но и стадий и на каждой такой стадии используется различные ср-ва производства, которые были произведены в др. отраслях.
Поэтому косвенные затраты отражают ту часть средств производства, которая была использована на предыдущих стадиях и входит в производство продукции не прямо, а через другие промежуточные средства производства. В отличие от прямых затрат, которые отражают кол-во средств производства, использованных непосредственно для изготовления.
Коэф. полных затрат bij показывают какой объем продукции i-ой отрасли необходимо произвести, чтобы с учетом прямых и косвенных затрат получить единицу продукции j-ой отрасли.
Коэф. полных мат.затрат можно применять с целью определения величины влияния на валовый выпуск определенной отрасли delXij некоторых изменений в объемах выпуска конечной продукции всех отраслей delYij
del 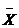 =
= 
Планування випуску на рівні галузі. Лінійні моделі економіки. Існування та єдність рішення у моделі МОБ.
Планирование выпуска на уровне отрасли.
Под балансовой моделью понимают систему уравнений, увязывающих материальные, трудовые и финансовые ресурсы с елью анализа перетока продукции между отдельными экономическими объектами (отраслями, регионами, предприятиями и их подразделениями), обеспечивающего такое функционирование производственного сектора, при котором имеет место баланс между объемом выпуска продукции и совокупной (производственной и конечной потребностью в ней).
Балансовые или матричные модели применяются для анализа и планирования производства и распределения продукции на различных уровнях иерархии от предприятия до макроэкономической системы в целом.
К наиболее распространенным видам относятся:
- частичные материальные, трудовые и финансовые балансы, относящиеся к народному хозяйству страны или отдельных регионов
- модели межотраслевого баланса производства и распределения продукции (МОБ);
- матричные техпрофин планы развития отраслей, предприятий и фирм.
Существование и единственность решение
В модели МОБ одним из наиболее существенных явл. вопрос о существовании и единств. решения.
Оно должно соответствовать реальным экон. процессам, а именно обеспечивать неотрицательность компонентов валового выпуска Х=(Х1 ….. Хn) Xi >= 0 , X>0 и вектора конечного выпуска Y.
Ответ на этот вопрос основан на сведениях линейной алгебры и на понятии продуктивности матрицы коэф. прямых мат.затрат.
Матрица А прямых мат.затрат состоит из элементов aij >=0 i,j = 1,n
Процесс воспроизводства нельзя осуществить, если бы для собственного производства в отрасли тратилось больше, чем создавалось.
Все диагональные элементы 0<= aij < 1 i=1,n
Определение
Модель Леонтьева называют продуктивной, если система Xi =  и
и
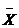 = А
= А 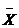 +Y имеет неотрицательно решение Хi>=0 i=1,n
+Y имеет неотрицательно решение Хi>=0 i=1,n
Или X>AX
Очевидно, что условие X>AX означает существование вектора конечного продукта
Y=(y1…yn) >0 yi>0 для МОБ
Из условий Х=(Е-А)-1*Y и Y=(E-A)*X следует, что какой бы вектор Х(Y) мы не взяли для того чтобы Y(x) было неотрицательным нужно, чтобы матрица (E-А)-1 или (E-А) была неотрицательно невырожденной матрицей.
Примичание: матрица неотрицательно невыраждена если она обратима, определитель det не равен 0 и обратная к ней неотрицательна В=(Е-А)-1 = (Е-А)T
Алгеброичное дополнение к aij – это минор к элементу aij*(-1) i+j
В свою очередь обратная матрица существует и неотрицательно определена, если все угловые миноры матрицы (Е-А) положительные
Из условия X>AX и определения собственного числа матрицы А
А*Х = 
Следовательно это наибольшее по модулю |  * | решение.
* | решение.
Наибольшее |  * | – корень характеристического уравнения может служить оценкой общего уровня коэффициентов прямых мат.затрат
* | – корень характеристического уравнения может служить оценкой общего уровня коэффициентов прямых мат.затрат
А величина 1-  * характеризует остаток после затрат, т.е продуктивность и чем больше величина 1-
* характеризует остаток после затрат, т.е продуктивность и чем больше величина 1-  * тем больше возможность для достижения других целей кроме производственного процесса.
* тем больше возможность для достижения других целей кроме производственного процесса.
Норма март.А – максимум суммы элементов матрицы по строчкам или по столбцам.
Норма должна быть < 1.
Дата добавления: 2018-02-15; просмотров: 99; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
