Практическое занятие №5«Выполнение тождественных преобразований в тригонометрических выражениях» 13 страница
Практическое занятие №12
«Решение задач на нахождение расстояний и углов в пространстве»
Практическое занятие рассчитано на 2 часа, относится к теме «Прямые и плоскости в пространстве».
Формируемые компетенции:У24, У25, У28, У29, У30, У31, З1, З2, З3
Цель:научиться решать задачи на нахождение углов и расстояний в пространстве, используя признаки и основные теоремы о параллельности; признаки перпендикулярности прямой и плоскости, теорему о трёх перпендикулярах.
Методическое и техническое обеспечение:
- методические указания к выполнению практического занятия;
- комплекты учебно-наглядных пособий по соответствующим разделам математики.
- мультимедийный проектор;
- ноутбук;
- проекционный экран;
- компьютерная техника для обучающихся с наличием лицензионного программного обеспечения;
- комплект слайд-презентаций.
Теоретические сведения
Две прямые называются параллельными, если они не имеют общих точек и лежат в одной плоскости.
Прямая и плоскость называются параллельными, если они не имеют общих точек ( 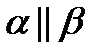 ).
).
a
b
α α α β
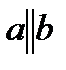 aa║αα║β
aa║αα║β
Две прямые в пространстве называются перпендикулярными, если угол между ними равен  (
( 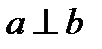 ).
).
Прямая называется перпендикулярной к плоскости, если она перпендикулярна к любой прямой, лежащей в плоскости  .
.
|
|
|
Прямая, пересекающая плоскость и не перпендикулярная ей, называется наклонной к плоскости.
Углом между прямой и плоскостью, пересекающей эту прямую и не перпендикулярную к ней, называют угол между прямой и её проекцией на плоскость.
a
φ 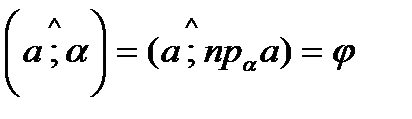
α 
Две пересекающиеся плоскости называются перпендикулярными, если угол между ними равен 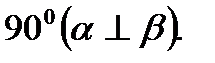
Признаки параллельности прямой и плоскости:
1. Если прямая, лежащая вне плоскости, параллельна какой-либо прямой, лежащей в этой плоскости, то она параллельна этой плоскости.
2. Если прямая и плоскость перпендикулярны одной и той же прямой, то они параллельны.
Признаки параллельности плоскостей:
1. Если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости, то эти плоскости параллельны.
2. Если две плоскости перпендикулярны одной и той же прямой, то они параллельны.
Признаки перпендикулярности прямой и плоскости:
1. Если прямая перпендикулярна двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна этой плоскости.
2. Если плоскость перпендикулярна одной из параллельных прямых, то она перпендикулярна и другой.
|
|
|
Теорема о трёх перпендикулярах.
Прямая, лежащая в плоскости и перпендикулярная проекции наклонной к этой плоскости, перпендикулярна и самой наклонной.
Признаки параллельности прямых в пространстве:
1. Если две прямые перпендикулярны одной и той же плоскости, то они параллельны.
2. Если в одной из пересекающихся плоскостей лежит прямая, параллельная другой плоскости, то она параллельна линии пересечения плоскостей.
Признак перпендикулярности плоскостей: если плоскость проходит через прямую, перпендикулярную другой плоскости, то эти плоскости перпендикулярны.
Пересечение двух полупространств, границами которых служат непараллельные плоскости, называется двугранным углом.
МN-ребро двугранного угла;
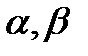 -грани; -грани;  ; ;
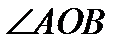 -линейный угол двугранного угла. -линейный угол двугранного угла.
|
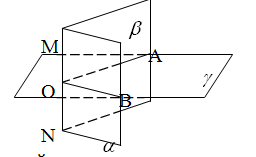
Двугранный угол измеряется своим линейным углом, т.е. 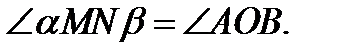
Две пересекающиеся плоскости определяют в пространстве четыре двугранных угла.
Две плоскости называют взаимно перпендикулярными, если угол между ними равен  (
( 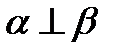 ).
).
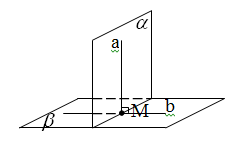
Теорема (признак перпендикулярности плоскостей).
Если плоскость проходит через перпендикуляр к другой плоскости, то она перпендикулярна этой плоскости
|
|
|
| Теорема. Если две плоскости взаимно перпендикулярны, то прямая, проведенная в одной плоскости перпендикулярно линии пересечения плоскостей, перпендикулярна другой плоскости. |
Пример выполнения задания
Пример №1. Дан прямоугольный параллелепипед 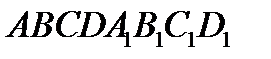 . Постройте его сечение плоскостью, проходящей через середины рёбер
. Постройте его сечение плоскостью, проходящей через середины рёбер 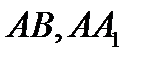 и
и 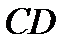 . Вычислите периметр сечения, принимая
. Вычислите периметр сечения, принимая 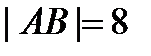 см,
см, 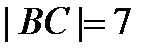 см,
см, 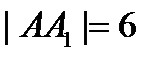 см.
см.
Дано: 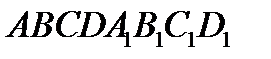 - прямоугольный параллелепипед. - прямоугольный параллелепипед.
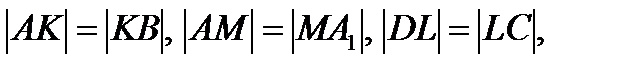
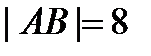 см, см, 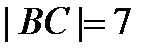 см, см, 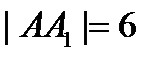 см.
Найти: см.
Найти: 
|
A1D1
MBNC
KL
AD
Решение.
Построим сечение.
1. соединим точки KиL ; K иM;
2. проведём 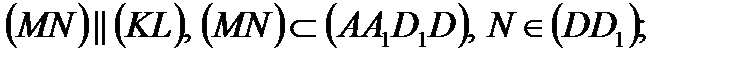
3. соединим точки LиM.
Плоскость 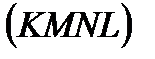 – искомое сечение, которое является прямоугольником.
– искомое сечение, которое является прямоугольником.
По условию 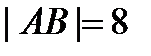 см
см 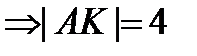 см,
см,
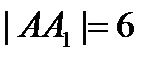 см
см  см.
см.
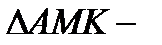 прямоугольный (т.к.
прямоугольный (т.к.  прямоугольный параллелепипед)
прямоугольный параллелепипед) 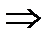 по т.Пифагора
по т.Пифагора 
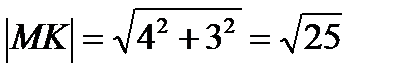
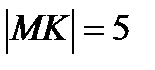 см.
см.

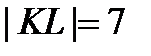 см, т.к.
см, т.к. 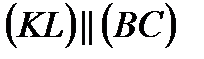
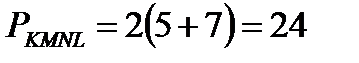 см
см
Ответ: 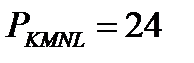 см.
см.
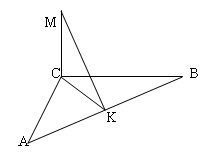 Пример №2.Из вершины прямого угла прямоугольного треугольника с катетами а и b, проведён перпендикуляр к плоскости треугольника. Длина перпендикуляра равна с. Найти расстояние от его концов до гипотенузы
Пример №2.Из вершины прямого угла прямоугольного треугольника с катетами а и b, проведён перпендикуляр к плоскости треугольника. Длина перпендикуляра равна с. Найти расстояние от его концов до гипотенузы
Дано:
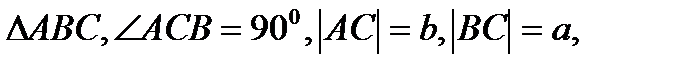
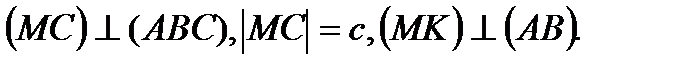
Найти: 
Решение.
1. 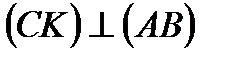 то теореме о трёх перпендикулярах
то теореме о трёх перпендикулярах 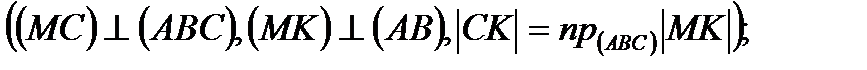
2.  ABC (
ABC (  – по условию) по т.Пифагора
– по условию) по т.Пифагора 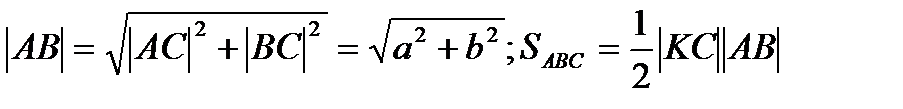 или
или 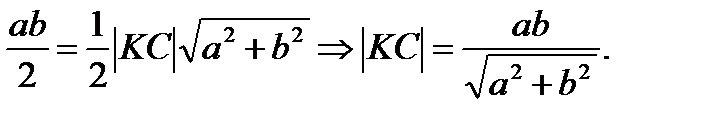
3.  MKC (
MKC ( 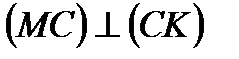 по опр.
по опр. 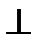 к плоскости
к плоскости  ) по т.Пифагора
) по т.Пифагора 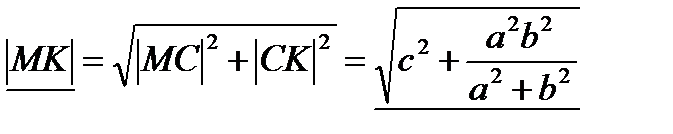 .
.
Ответ: 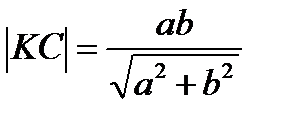 ;
; 
Пример №3.
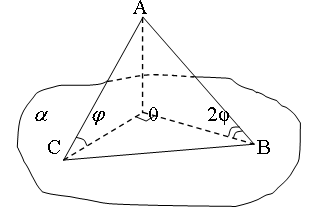 Прямая AC наклонена к плоскости
Прямая AC наклонена к плоскости  под углом
под углом 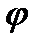 ,прямая AB под углом 2
,прямая AB под углом 2  .Меньший из отрезков AC и AB, где
.Меньший из отрезков AC и AB, где 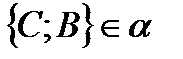 , равен а. Найти BC, если известно, что проекции наклонных взаимно перпендикулярны.
, равен а. Найти BC, если известно, что проекции наклонных взаимно перпендикулярны.
|
|
|
Дано:
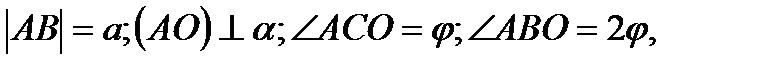
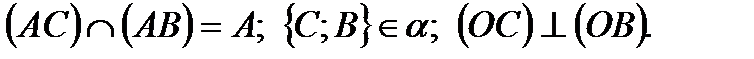
Найти: 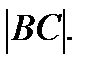
Решение.
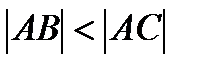 (
(  следовательно, против меньшего угла лежит меньшая сторона, т.е.
следовательно, против меньшего угла лежит меньшая сторона, т.е. 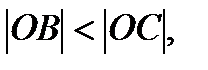 а т.к. АО – общая
а т.к. АО – общая  АОС и
АОС и  АОВ, то по т. Пифагора
АОВ, то по т. Пифагора 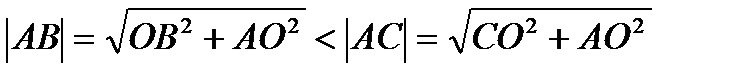 )
)
1.  АОВ (
АОВ ( 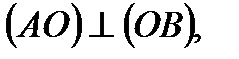 т.к.
т.к. 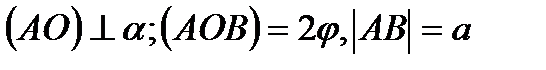 - по условию)
- по условию)
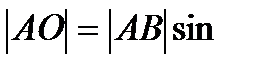
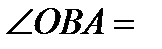
 ;
;
2.  АОС (
АОС ( 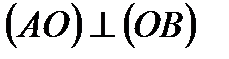 , т.к.
, т.к.  - по условию;
- по условию; 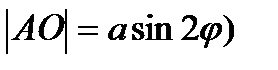
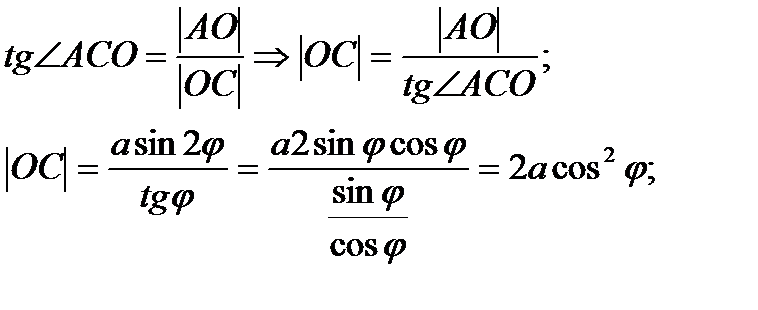
3.  СОВ (
СОВ ( 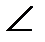
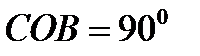 - по условию,
- по условию, 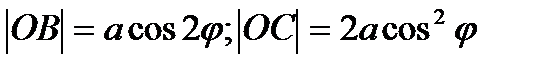 )
)
По т.Пифагора 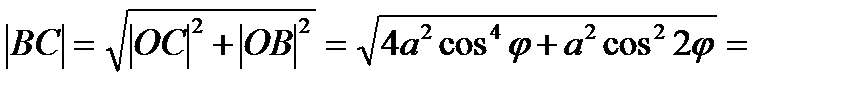
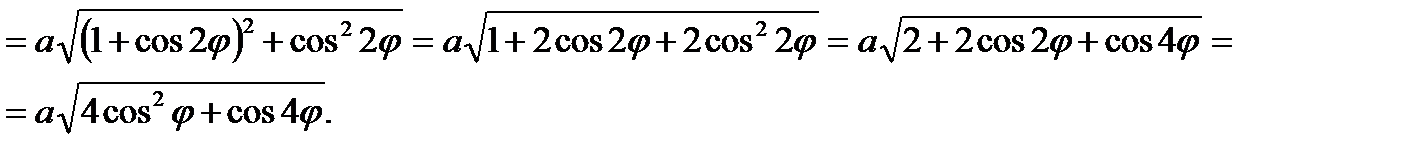
Ответ: 
Пример №4 На грани двугранного угла величиной 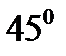 дана точка, удаленная от ребра на расстояние а. Найти расстояние от этой точки до другой грани.
дана точка, удаленная от ребра на расстояние а. Найти расстояние от этой точки до другой грани.
Дано: 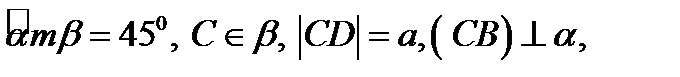
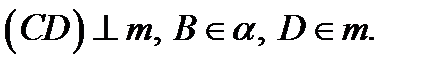 Найти:
Найти: 
|
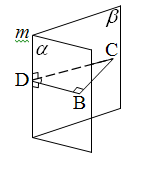
Решение.
По теореме о трёх перпендикулярах  Тогда
Тогда  линейный угол данного двугранного угла, т.е.
линейный угол данного двугранного угла, т.е.  Из прямоугольного
Из прямоугольного 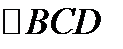 получим:
получим:
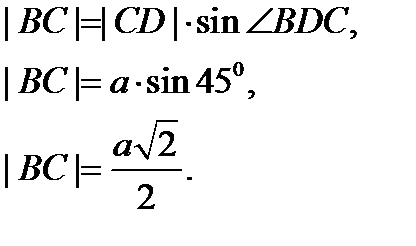 Ответ:
Ответ: 
Пример №5. Катеты прямоугольного треугольника равны а и 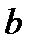 .Определить расстояние от вершины прямого угла до плоскости, которая проходит через гипотенузу и составляет угол в 300 с плоскостью треугольника.
.Определить расстояние от вершины прямого угла до плоскости, которая проходит через гипотенузу и составляет угол в 300 с плоскостью треугольника.
Дано: 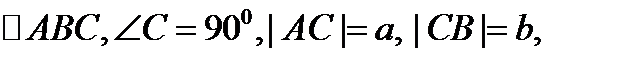
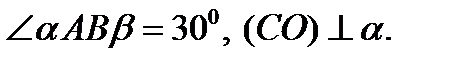 Найти:
Найти: 
|
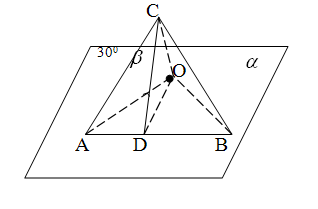
Решение.
Проведём  По теореме о трёх перпендикулярах
По теореме о трёх перпендикулярах 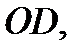 как проекция наклонной
как проекция наклонной 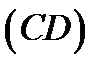 на плоскость
на плоскость 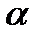 , будет перпендикулярна к
, будет перпендикулярна к 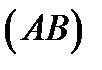 . Тогда
. Тогда 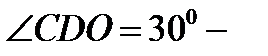 будет линейным углом двугранного угла
будет линейным углом двугранного угла  .
.
Из 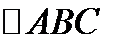 по теореме Пифагора:
по теореме Пифагора: 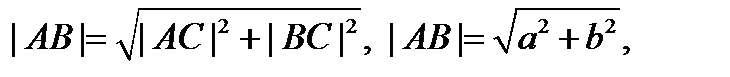
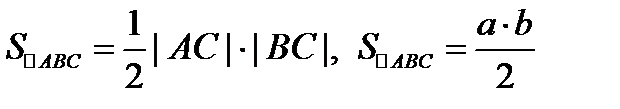 . С другой стороны,
. С другой стороны, 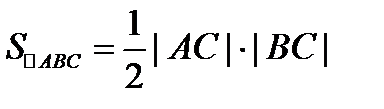 или
или 
 (как катет, лежащий против угла в 300 в
(как катет, лежащий против угла в 300 в 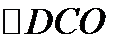 )
)
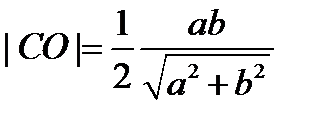 .
.
Ответ: 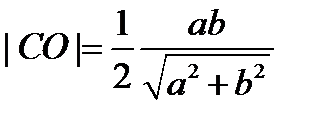 .
.
Пример №6. Данный отрезок имеет концы на двух взаимно перпендикулярных плоскостях и составляет с одной из них угол в 450, а с другой – угол в 300; длина этого отрезка равна  . Определить часть линии пересечения плоскостей, заключённую между перпендикулярами, опущенными на неё из концов данного отрезка.
. Определить часть линии пересечения плоскостей, заключённую между перпендикулярами, опущенными на неё из концов данного отрезка.
Дано: 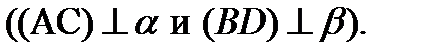
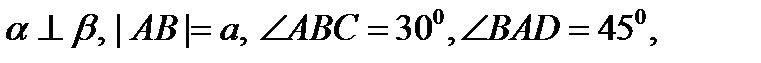 Найти:
Найти: 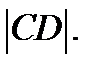
|
 Решение.
Решение.
Из 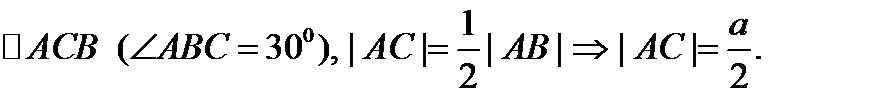
Из 
Тогда из прямоугольного 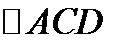 находим по следствию из теоремы Пифагора:
находим по следствию из теоремы Пифагора:
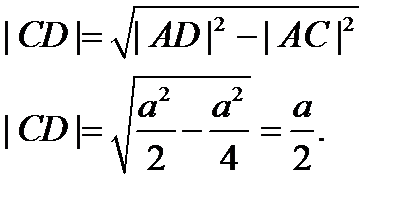 Ответ:
Ответ: 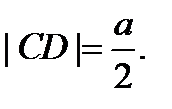
Дата добавления: 2021-07-19; просмотров: 121; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
