Понятие о длинных и коротких оболочках.

В зависимости от характера работы под нагрузкой оболочки условно разделяют на длинные, отношение пролета которых l1 к длине волны l2 более 4, средней длины при 1<l1/l2<4, и короткие при l1/l2≤1. Первые два вида обычно объединяют одним наименованием — длинные оболочки.

Длинные цилиндрические оболочки.

Если зоны действия краевого эффекта по краям оболочки не перекрывают друг друга, то оболочка называется длинной

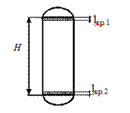
Короткие цилиндрические оболочки.

Оболочка короткая, если зоны накладываются друг на друга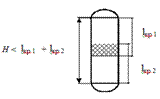

99. МЕТОДЫ ОПРЕДЕЛЕНИЯ КРАЕВЫХ НАГРУЗОК ( В ТОМ ЧИСЛЕ РАСПОРНОЙ СИЛЫ), ВОЗНИКАЮЩИХ В УЗЛАХ СОПРЯЖЕНИЯ ТОНКИХ ОБОЛОЧЕК, НАХОДЯЩИХСЯ ПОД ВОЗДЕЙСТВИЕМ ВНУТРЕННЕГО ДАВЛЕНИЯ (ПРИВЕСТИ ПРИМЕРЫ РАСЧЕТНЫХ СХЕМ И ПРАВИЛО ЗНАКОВ).

Определение краевых нагрузок

Для нахождения краевых нагрузок составляется расчетная схема узла сопряжения (рисунок 3). Нагрузки Q₀ и M₀ определяются из уравнений совместности деформаций. Учитывая, что в узле сопряжения деформации краев оболочек одинаковы, в общем виде можно записать:  

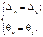(1)

Это уравнение решается с использованием принципа независимости действия сил, то есть находятся деформации отдельно от каждой нагрузки и тогда уравнение переписывается в следующем виде (2)

где 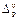, , 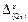, , 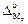,  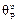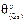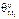– соответственно радиальные (м) и угловые (рад) деформации края цилиндрической обечайки под действием нагрузок Р, Q₀, М₀ 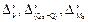,  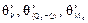– соответственно радиальные (м) и угловые (рад) деформации эллиптической обечайки под действием нагрузок Р, Q₀, М₀.

При составлении данного уравнения применяется следующее правило знаков: линейные перемещения считаются положительными, если от рассматриваемой нагрузки край оболочки перемещается в направлении от оси.

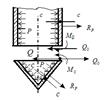
Рис. 3 – Расчетная схема для определения краевых нагрузок

Угловые перемещения считаются положительными, если внешняя нагрузка создаёт момент, направленный по часовой стрелке, относительно рассматриваемого сечения (например, сечение с – с, рисунок 3).

При этом в первом приближении принимается, что Q₀ >Q.

Для рассматриваемого случая уравнение (2) будет иметь следующий вид

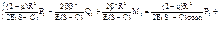
Аналогично записывается уравнение для углов поворота, решаются два уравнения с двумя неизвестными и находятся значения Q₀ и M₀.

Определение распорной силы

В том случае, когда обечайки соединены под углом, т.е. не имеют общей касательной в узле сопряжения кроме краевых нагрузок Q₀ и M₀, возникает так называемая распорная сила Q, равномерно распределенная по краю.

Рассмотрим условие ее появления и получим зависимость, по которой она может быть определена, например, для конической обечайки. Как известно, в конической обечайке возникает продольная меридиональная сила U_x. Разложим ее на составляющие U^’_к и Q.

При этом доказано, что U^’_ц = U^’_к

где U^’_ц – меридиональная (продольная) сила, возникающая в цилиндрической обечайке под действием внутреннего давления.

Таким образом, и U^’_ц и U^’_к, взаимокомпенсируются, так как они направлены навстречу друг другу и равны между собой. В этом случае остается нескомпенсированной сила Q, так называемая распорная сила. Она как бы распирает обечайку, вызывая появление дополнительных деформаций и напряжений. Поэтому при конструировании конических днищ желательно, чтобы распорная сила была как можно меньше.Откуда путем несложных преобразований находим величину распорной силы .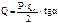 

100. ОСНОВЫ МОМЕНТНОЙ ТЕОРИИ РАСЧЕТА ТОНКОСТЕННЫХ ОБОЛОЧЕК, НАХОДЯЩИХСЯ ПОД ВОЗДЕЙСТВИЕМ ВНУТРЕННЕГО ДАВЛЕНИЯ. ВНУТРЕННИЕ СИЛОВЫЕ ФАКТОРЫ (ВСФ) И НАПРЯЖЕНИЯ, ВОЗНИКАЮЩИЕ В ЭЛЕМЕНТЕ СТЕНКИ ОБОЛОЧКИ, ПРИ РАСЧЕТЕ ПО МОМЕНТНОЙ ТЕОРИИ (ПРИВЕСТИ РИСУНОК ЗОНЫ ДЕЙСТВИЯ КРАЕВОГО ЭФФЕКТА (ЗДКЭ) И ЭЛЕМЕНТА С ВСФ). ХАРАКТЕР ИЗМЕНЕНИЯ ВСФ И НАПРЯЖЕНИЙ ВДОЛЬ ЗДКЭ. КОЭФФИЦИЕНТ ЗАТУХАНИЯ.

В колонных аппаратах имеются такие узлы, где появляются так называемые краевые нагрузки, от которых возникают дополнительные внутренние силовые факторы, в том числе и изгибающие моменты, напряжения от которых могут достигать значительных величин и ими нельзя пренебречь.

Такая теория расчета, при которой учитываются напряжения от изгибающих моментов, называется моментной теорией. При этом краевые напряжения могут достигать высоких значений, поэтому необходимо уметь определять эти величины и принимать конструктивные меры для их снижения. Таким образом, цель расчета по моментной теории заключается в определении краевых нагрузок Q₀ и M₀, в расчете дополнительных внутренних силовых факторов и определении суммарных напряжений от давления и краевых нагрузок. Затем по максимальным напряжениям проверяется прочность оболочки в узле сопряжения. Если условие прочности не выполняется, увеличивается толщина стенки и весь расчет повторяется.

Краевые напряжения особенно опасны в аппаратах, изготовленных из хрупких материалов, таких, как кремнистый чугун, термореактивные пластмассы, керамика и т.д., а также в аппаратах, подверженных знакопеременным нагрузкам.

Внутренние силовые факторы

Какие внутренние силовые факторы возникают в оболочке под действием внутреннего давления Р_внутр?

Для решения этой задачи рассмотрим пример – воздушный шарик, находящийся под действием газового давления.

 

T, U– тангенциальные и меридиональные растягивающие усилия;

M_t, M_m – тангенциальный и меридиональный изгибающий моменты;

P – усилие от давления.

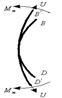
Изобразим деформации стенки сферы

Допустим, надули шарик до давления P₁ и он принял определенный размер, характеризующийся длиной окружности поперечного сечения.

Надуваем шарик до давления P₂> Р₁, размеры шарика увеличиваются и, соответственно, изменяются размеры дуги AB.

Из рисунка видно, что дуги не совпадут, так как, во-первых, одна дуга длиннее другой, т.е. на нее должны действовать растягивающие усилия, в данном случае тангенциальные – T , а во-вторых, различна их кривизна.

Изменить свою кривизну дуга может только под действием изгибающих моментов. Для рассматриваемого случая это – М_t.

Если шарик повернуть на 90°, то параллельный круг превратится в меридиан.

Для дуги BD будут происходить аналогичные изменения, т.е. на эту дугу будут действовать меридиональные растягивающие усилия U и меридиональный изгибающий момент M_m

Таким образом, в оболочках под действием внутреннего давления возникают усилия U и T и изгибающие моменты М_t, М_m.

Доказано, что в случае, когда вдоль меридиана не будет резких изменений внешней нагрузки, толщины оболочки и ее радиусов кривизны, то можно принять, что оболочка не подвергается изгибу, т.е. изгибающие моменты и поперечная сила равны нулю (М_x = М_y = О_y = 0), благодаря же симметрии формы и нагрузки оболочки действие крутящих моментов М_z и поперечной силы О_x на всех гранях исключено и тогда касательные напряжения отсутствуют.

Таким образом, по граням действуют только нормальные усилия N; будем называть их соответственно меридиональными и обозначать N = U и тангенциальными N = Т (по граням АС и ВД). От них возникают нормальные напряжения, соответственно - меридиональные s_m и тангенциальные s_t

Кроме этого на грань АВСД действует внешняя нагрузка Р. (В данном примере это внутренне избыточное давление). От этой нагрузки возникает, так называемое, радиальное напряжение, направленное вдоль радиуса оболочки и равное по величине давлению, т. е. s_r = Р. для тонкостенных оболочек давление меньше 10 МПа, значительно меньше допускаемых напряжений, радиальные напряжения принимают равными нулю.

Расчет длинных оболочек по моментной теории

---

Дата добавления: 2019-11-25; просмотров: 697; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!