Область применения. Причины и п ризнаки деления сосудов на тонко- и толстостенные
В осесимметричных оболочках, находящихся под действием внутреннего давления Р, в самом общем случае в стенках аппаратов возникают тангенциальные σt, меридианальные σm, и радиальные σrнапряжения.
Для тонкостенных аппаратов 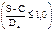 при расчете напряжений принимали, что:
при расчете напряжений принимали, что:
- распределение тангенциальных (кольцевых) напряжений равномерно по толщине стенки;
- радиальным напряжением, максимальное значение которого не превышают 10 МПа, т.е. σr≤Р (т.к. для тонкостенных обычно Р< 10 МПа), можно пренебречь. В этом случае напряженное состояние материала оболочек – плоское (двухосное).
Для толстостенных оболочек нельзя принимать распределение σt по толщине стенки равномерным и пренебрегать радиальным напряжением, т.к. давление может достигать порядка 600 МПа и тогда σr =600МПа (на внутренних волокнах), что значительно больше допускаемых напряжений и соизмеримо с σt. В этом случае напряженное состояние материала оболочек - объемное (трехосное).
Таким образом, основными причинами, по которым аппараты подразделяются на тонко- и толстостенные являются:
1) отличие напряженных состояний материала оболочек:
- для тонкостенных – двухосное (σr ≈ 0; σm ≠ 0; σt ≠ 0);
- для толстостенных – объемное (σr ≠ 0; σm ≠ 0; σt ≠ 0);
2) различный характер распределения тангенциальных напряжений по толщине стенки:
- для тонкостенных - равномерное;
- для толстостенных - неравномерное.
|
|
|
Основными признаками деления сосудов на тонко- и толстостенные являются соотношение толщины стенки S к внутреннему диаметру Dв. и значение давлений, т.е.
- для тонкостенных:
а) 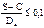 (при Dв.>200мм) или
(при Dв.>200мм) или 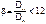 ,
,
где β - коэффициент толстостенности;
б) Р≤ 10 МПа (условное разделение);
- для толстостенных:
а) 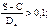
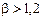 ,
,
б) Р> 10 МПа.
К аппаратам высокого давления.как было сказано ранее, относят аппараты, работающие под давлением свыше 10 МПа. Толщина стенки корпуса такого аппарата превышает 10 % его внутреннего диаметра, т.е. коэффициент толстостенности (отношение наружного диаметра к внутреннему) 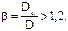
Цель расчета толстостенных аппаратов заключается в получении формул для нахождения напряжений σr, σm, σt .
Для нахождения этого рассмотрим толстостенную цилиндрическую оболочку без днищ, нагруженную равномерно распределенными по высоте и периметру внутренним Р и наружным q давлениями (рисунок 3.2). При этом если аппарат не имеет днищ то σm=0. Следовательно, необходимо получить формулы для расчета σr и σt.
Расчленим оболочку на бесконечное число полосок и выделим одну из них (рисунок 3.3) сечениями I-I и II-II. Как видно из рисунка, расчетная схема такой полоски аналогична схеме нагружения тонкой жесткой пластины радиальными нагрузками (см. теорию расчета тонких жестких пластин).
|
|
|

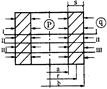
Рисунок 3.2
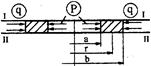
Рисунок 3.3
Поэтому в данном случае может быть применен метод начальных параметров, используемый при расчете таких пластин, согласно которому напряжения σr и σtопределяются по следующим формулам:
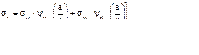
Начальные параметры 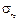 и
и 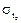 находим из граничных условий:
находим из граничных условий:
а) при r = а, 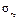 = -Р;
= -Р;
б) при r = b, 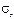 = -q.
= -q.
Используя граничное условие б), определяем значение 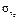 , т.е. при r = b, σr= -q:
, т.е. при r = b, σr= -q:
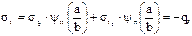
 откуда
откуда 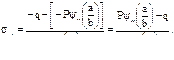 (3.2)
(3.2)
Подставляя 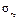 и
и 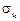 в уравнения (3.1) и расшифровывая сопровождающие функции
в уравнения (3.1) и расшифровывая сопровождающие функции
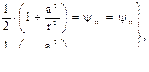
получим выражения для определения напряжений:
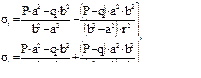
Если цилиндрическая обечайка имеет днища, то при действии на них внутреннего и наружного давлений возникает меридиональная сила U (рисунок 3.4) и соответственно меридиональное напряжение σm.
Рисунок 3.4
Для его нахождения рассмотрим равновесие отсеченной части. Составим сумму проекций всех сил на ось X и приравняем нулю.
ΣX = 0.
От Р и q возникают усилия, равные произведению Р и q соответственно на проекцию поверхностей радиусами а и b на плоскость, перпендикулярную оси Х. Проекции поверхностей, на которые действуют давления Р и q, на плоскость, перпендикулярную оси Х, представляют площади окружностей πа2 и πb2, т.е.
|
|
|

Напряжение σm определяется по формуле
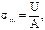
где 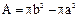 - площадь кольца,
- площадь кольца,
т.е. 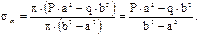
Распределение напряжений σ r , σ m , σ t по толщине стенки под действием внутреннего давления
Обычно q = 0, тогда уравнения (3.3) и (3.4) упрощаются:
 (3.5)
(3.5)
Сравнивая σmс суммой напряжений (σt+σr), получим зависимость, связывающую все три напряжения между собой, т.е.
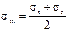 (3.6)
(3.6)
Рассмотрим распределение напряжений по толщине стенки в сечении, например, I-I (рисунок 4.1).
Рисунок 4.1
Для этого проанализируем формулы (3.5 и 3.6). Как видно, σr, σt для какого-то конкретного аппарата (т.е. при заданныхa, b, P) зависит только от текущего радиуса, т.е.
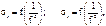
а σm – постоянна по толщине стенки.
Сопоставим между собой σrи σt. Для этого определим эти напряжения при r = a и r = b: а) r=a,
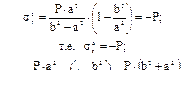
Так как (b2+a2) > (b2-a2), то при r = a σt>0 и 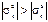 , а меридиональное напряжение равно
, а меридиональное напряжение равно
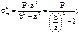
так как для толстостенных аппаратов

где β – коэффициент толстостенности, то, например, при β = 1,5, значение меридионального напряжения при r = a составит
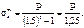
|
|
|
Таким образом, анализ напряжений, действующих на внутренних волокнах, показывает, что
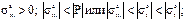
б) r=b,
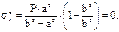
На сколько отличаются тангенциальные напряжения при r=b и r=a? Для этого найдем величину 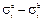 :
:
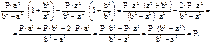
Таким образом, 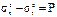 .
.
Сравнение так же показывает, что 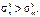
По данным этого раздела строим эпюры σm, σt, σr (рисунок 4.2).
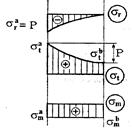
Рисунок 4.2
Таким образом, анализ изменения этих напряжений по толщине стенки показывает, что по абсолютному значению σt и σr максимальны на внутренних волокнах, σm - постоянны по S.
103. ТОЛЩИНА СТЕНКИ ОДНОСЛОЙНОГО (МОНОЛИТНОГО) ЦИЛИНДРИЧЕСКОГО СОСУДА, НАХОДЯЩЕГОСЯ ПОД ВОЗДЕЙСТВИЕМ ВНУТРЕННЕГО ИЗБЫТОЧНОГО ДАВЛЕНИЯ (БЕЗ ВЫВОДА). АНАЛИЗ И ОБЛАСТЬ ПРИМЕНЕНИЯ ФОРМУЛЫ С ЧИСЛОВЫМИ ПРИМЕРАМИ. МЕТОДЫ ПОВЫШЕНИЯ НЕСУЩЕЙ СПОСОБНОСТИ ОДНОСЛОЙНЫХ СОСУДОВ (ПЕРЕЧИСЛИТЬ, БЕЗ ОПИСАНИЯ).
Толщина стенки однослойного (монолитного) цилиндрического сосуда, находящегося под воздействием внутреннего избыточного давления (без вывода). Анализ и область применения формулы с числовыми примерами.
Расчет выполняется либо для рабочих условий, либо для рабочих условий и условий испытаний.Расчет на прочность цилиндрических обечаек и выпуклых днищ для условий испытаний проводить не требуется, если выполняется условие
Рирас< 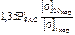 .
.
Расчетная толщина стенки цилиндрической обечайки Sц р и днищ Sднр для рабочих условий и условий испытания (без учета суммы прибавок С) представлены в таблице
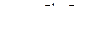 (1)
(1)
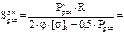 (2)
(2)
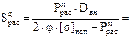 (3)
(3)
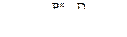 (4)
(4)
| Цилиндрическая обечайка | Днище | ||
| Расчетная толщина стенки цилиндрической обечайки для рабочих условий без учета суммы прибавок С, Sц рас , мм | 1 | Расчетная толщина стенки днища для рабочих условий без учета суммы прибавок С, Sднрас , мм | 2 |
| Расчетная толщина стенки цилиндрической обечайки для условий гидроиспытаний без учета суммы прибавок С, Sц рас , мм | 3 | Расчетная толщина стенки днища для условий гидроиспытания без учета суммы прибавок С, Sднрас , мм | 4 |
Методы повышения несущей способности однослойных сосудов (перечислить, без описания).
Существует два метода увеличения несущей способности:
1) создание многослойных сосудов;
2) метод автофреттирования (автокрепления; самокрепления).
Дата добавления: 2019-11-25; просмотров: 419; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
