МЕТОДИКА И ЦЕЛЬ СОЗДАНИЯ МНОГОСЛОЙНЫХ СОСУДОВ. УСЛОВИЕ ОПТИМАЛЬНОСТИ МНОГОСЛОЙНЫХ СОСУДОВ, НАХОДЯЩИХСЯ ПОД ВОЗДЕЙСТВИЕМ ВНУТРЕННЕГО ДАВЛЕНИЯ. ТОЛЩИНА СТЕНКИ МНОГОСЛОЙНЫХ СОСУДОВ.
Методика и цель создания многослойных сосудов.
В химическом машиностроении в последние годы проектируются аппараты на так называемые сверхвысокие давления, при которых применение обычных толстостенных сосудов становится невозможным иливследствие отсутствия достаточно прочного материала или же из-за крайней трудности и даже невозможности практически изготовить соответствующий сосуд (если такой материм имеется) вследствие чрезмерной толщины стенки.
Например, при давлении ваппарате Р=600 МПа (колонна синтеза аммиака), [σ]=1400 МПа и Dв.=2 м толщина стенки должна быть равна
что нереализуемо на практике. В этом случае разрабатываются, так называемые, многослойные аппараты.
Существует два метода увеличения несущей способности:
1) создание многослойных сосудов;
2) метод автофреттирования (автокрепления; самокрепления).
Условие оптимальности многослойных сосудов, находящихся под воздействием внутреннего давления.
Сосуд считается спроектированным оптимально, если эквивалентные напряжения на внутренних радиусах каждого цилиндра равны между собой, т.е. в этом случае достигается равномерное распределение напряжений по толщине стенки. Для двухслойного сосуда условие оптимальности выполняется, если эквивалентные напряжения в точках А и В будут равны, т.е. (рисунок 4.1)
.
Из этого условия ученый Гадолин определил оптимальное соотношение между радиусами внутренним а, наружным b и радиусом сопряжения двух сосудов с, т.е.
|
|
|
Соотношение Гадолина (4.2) справедливо, если двухслойный цилиндр изготовлен из одного материала
Рисунок 4.1 -
Проверим, оптимально ли спроектирован сосуд в рассмотренном примере.
По условию задачи с = 0,144 м, таким образом, сосуд спроектирован оптимально (при заданных а и b).
Если слоев больше чем два, то соотношение Гадолина для любого числа слоев имеет вид
где n - число слоев;
ri - радиус сопряжения i-го слоя.
Толщина стенки многослойных сосудов.
Определяется следующим образом (по III теории прочности):
(4.4)
или по IV теории прочности
(4.5)
Задача о расчете толстостенного цилиндра решается с учетом равномерно распределенного наружного давления 
и внутреннего давления 
. Мы исходим из того, что такая нагрузка не может вызвать деформации изгиба цилиндра.
Нормальные напряжения 
в сечениях плоскостями, перпендикулярными оси симметрии О цилиндра нельзя считать равномерно распределенными по толщине стенки, как это делается при расчете тонкостенных оболочек вращения (рис.16.6).
Нормальные напряжения 
действующие по цилиндрической поверхности с радиусом 
могут быть одного и того же порядка и даже превышать напряжение 
, что при тонкостенных цилиндрах невозможно. 
|
|
|
Рис.16.6
В поперечных сечениях цилиндра касательные напряжения также предполагаются равными нулю, однако, возможно существование нормальных осевых напряжений 
, которые возникают как следствие нагруженияцилиндра силами, действующими вдоль оси. В дальнейшем мы будем рассматривать открытые цилиндры, т.е. не имеющие днищ. Напряжения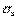 
в таких цилиндрах равны нулю. Вывод формул расчета напряжений в толстостенных цилиндрах основан на том, что для них соблюдается гипотеза плоских сечений, т.е. поперечные сечения цилиндра, плоские до нагружения, останутся плоскими и после нагружения.
Основными уравнениями для расчета напряжений в толстостенных цилиндрах являются формулы Ламе:
,
.
При действии на цилиндр только наружного или внутреннего давления знаки эпюр 
, 
во всех точках цилиндра одинаковы. Эпюры изменения радиального 
и окружного напряжения 
для случая действия только наружного давления показаны на рис.16.7. Эти напряжения во всех точках цилиндра отрицательны, что соответствует сжатию.
Рис.16.7 Рис.16.8
При нагружении внутренним давлением эпюры изменения радиального окружного напряжения показаны на рис.16.8. Окружное напряжение является расширяющим, а радиальное сжимающим.
|
|
|
Анализ формул Ламе показывает, что увеличение толщины не может во всех случаях обеспечить необходимой прочности цилиндра. Поэтому для сосудов высокого давления необходимо искать какие-то другие конструктивные решения. Одним из таких решений является создание составных, соединенных с натягом, цилиндров. Этот прием используется как в технике высоких давлений, так и в артиллерийской практике для упрочнения стволов мощных орудий.
В результате натяга в трубах возникают нормальные напряжения, которые частично компенсируют напряжения в трубе от действия высокого давления.
АВТОФРЕТТИРОВАНИЕ СОСУДОВ
При повышении внутреннего давления однослойного цилиндра напряжения возрастают. Если в сосуде давление (Рт) возрастет настолько, что напряжения на внутренних слоях, где они максимальны, будут превосходить предел текучести σт, материал этих слоев начинает течь. Слои же, в которых напряжения остаются ниже предела текучести σт, остаются упругими. Очевидно, что если бы напряжения во внутренних слоях превысили предел прочности, то и тогда эти слои, не могли бы разрушиться, т.к. этому воспрепятствуют внешние слои, оставшиеся упругими.
|
|
|
Если, не доведя трубу до разрыва, мы начнем уменьшать давление, то та часть стенки, которая пришла в пластическое состояние, (т.е. напряжения в ней равны σт) (рисунок 5.1), будет иметь остаточные деформации εост и ее радиус “с” будет стремиться оставаться несколько больше первоначального (рисунок 5.2). Что касается наружных слоев, то они будут стремиться вернуться в первоначальное состояние, т.к. они остались упругими (т.е. εост =0). Так как этому будут препятствовать внутренние слои, то они будут сжиматься наружными.
Рисунок 5.1 -
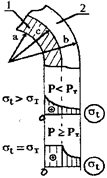
1 – пластичная зона; 2 – упругая зона
Рисунок 5.2 –
А слоям будут препятствовать вернуться в исходное состояние внутренние слои, поэтому внешние слои окажутся несколько растянутыми, т.е. наблюдается картина, аналогичная двухслойным сосудам при надевании их друг на друга с натягом и создании монтажного давления – Рм..
Если же после этого нагружать трубу рабочим давлением Р, напряжения σr, σt, возникающие от него, будут складываться алгебраически с напряжениями, возникающими при автофреттаже. В результате произойдет более благоприятное перераспределение напряжений, аналогичное картине, наблюдаемой на рисунке 3.4.
Эти факты привели к мысли об использовании остаточных деформаций для повышения прочности однослойных сосудов и к созданию процесса производства последних, который называется автофреттированием или автокреплением труб.
Больше всего автофреттаж находит применение в производстве артиллерийских орудий.
Дата добавления: 2019-11-25; просмотров: 512; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!