Сравнение результатов расчета для толстостенных и тонкостенных сосудов
Для тонкостенных и толстостенных сосудов максимальные напряжения σt, причем для толстостенных  при r = а, т.е. на внутренних волокнах. Поэтому сравнение результатов расчета для обоих типов аппаратов проведем по σt.
при r = а, т.е. на внутренних волокнах. Поэтому сравнение результатов расчета для обоих типов аппаратов проведем по σt.
Для тонкостенного сосуда:
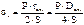
Выразим: S=b-a; Dс.п.=2a+b-a=a+b, тогда

Для толстостенных сосудов при r=a:
 .
.
Определим отношение 
 . (52)
. (52)
Ранее было принято, что  означает коэффициент толстостенности.
означает коэффициент толстостенности.
Напомним, что для тонкостенных сосудов β≤1,2;
для толстостенных сосудов β>1,2.
Подставив в уравнение (45) вместо  коэффициент β, получим
коэффициент β, получим

Сравним величины тангенциальных напряжений при разных β:

то есть, чем больше β, тем значительнее отличаются напряжения, определенные по формулам для тонкостенных и толстостенных сосудов.
Сравним, как отличаются толщины стенок, рассчитанные по формулам для тонкостенных и толстостенных сосудов при Р>10 МПа. Например:
Dв.=2,0 м; [σ]=200 МПа; φ=1,0.
| P, МПа | Тонкостенные сосуды | Толстостенные сосуды | расх., % | |
| 10 |
| 
| 5,5 | |
| 20 | S=0,105 м | S=0,118 м | 11 | |
| 90 | S=0,58 м | S=2,162 м | 73 | |
Таким образом, с увеличением давления расхождение значений S, найденных по формулам для толстостенных и тонкостенных сосудов, достигает недопустимых пределов. Поэтому, если при Р>10 МПа применить формулы для расчета тонкостенных сосудов, это может привести к существенным ошибкам при конструировании и к разрушению аппарата при его эксплуатации.
|
|
|
СВОБОДНЫЕ КОЛЕБАНИЯ СТЕРЖНЯ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ.
При эксплуатации химических, а также и других машин и аппаратов, очень часто приходится встречаться с колебательным движением механических систем: высокий колонный аппарат колеблется под действием порывов ветра и т. д. . Во всех этих случаях колеблющееся тело периодически перемещается между крайними положениями, проходя одну и ту же точку то в одном, то в другом направлении через примерно одинаковые промежутки времени (период колебаний), т. е, совершает механические колебания.
Колебательные движения упругой системы с переходом ее от одного крайнего положения к другому, происходящие при отсутствии переменных внешних сил, называются свободными или собственными колебаниями. В отличие от них вынужденными колебаниями называются колебания систем, происходящие при действии на нее переменных внешних (возмущающих) сил.
Продольные колебания - поперечные сечения стержня колеблются вдоль оси стержня около положения равновесия. Стержень то укорачивается, то удлиняется в пределах упругих деформаций.
Крутильные колебания - поперечные сечения стержня поворачиваются вокруг его оси то в одну, то в другую сторону на некоторый угол ф, оставаясь в своей плоскости: диск на конце консоли, закрученной и предоставленной далее самой себе.
|
|
|
Поперечные или изгибные колебания-сечения стержня смещаются нормально к его оси поочередно то в одну, то в другую сторону от положения равновесия, поворачиваясь при этом вокруг своих нейтральных осей на угол 0. Этот вид колебаний по сравнению с первыми двумя наиболее часто встречается на практике.
Круговая частота – число циклов колебаний укладывающиеся в 2π.
Период колебаний – связано с продолжительностью одного цикла колебаний.
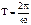 Амплитуда - наибольшее отклонение от положения равновесия.
Амплитуда - наибольшее отклонение от положения равновесия.

Колебание с 1 степенью свободы
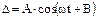
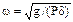
где А, В – постоянные интегрирования


ВАЛЫ, КЛАССИФИКАЦИЯ ВАЛОВ
1) в зависимости от количества установленных на валу деталей (дисков, шкивов, муфт, колес, мешалок и так далее). Различают валы
– с одной сосредоточенной массой;
– со многими сосредоточенными массами (рисунок 1, а;1, б).
При этом относительно менее массивные элементы полагают лишенными массы, а масса самого вала в зависимости от метода расчета может быть представлена либо в виде равномерно распределенной нагрузки, либо сосредоточенной распределенной между другими сосредоточенными массами. Масса вала может и не учитываться, если она составляет менее 30% массы детали вала (диска, барабана и так далее).
|
|
|
2) по виду поперечного сечения различаю валы:
– постоянного поперечного сечения;
– переменного поперечного сечения (рисунок 1, в).
3) в зависимости от места установки подшипников валы подразделяют на:
– однопролетные (рисунок 1, г);
– консольные (рисунок 1, д);
– многопролетные (неразрезные).
Расчет многопролетных валов принципиально ничем не отличается от расчета однопролетных валов, однако практически задача значительно и для машиностроения представляет ограниченный интерес.
4) по характеру опор (подшипников) различают валы:
– с короткими опорами, для которых центр опорного шарнира соответствует на расчетной схеме середине подшипника (рисунок 2 ).
К таким относятся одиночные подшипники качения, сдвоенный подшипник качения при условии самоустанавливаемости всего блока опоры, самоустанавливающийся подшипник скольжения при  и несамоустанавливающийся короткий подшипник скольжения при
и несамоустанавливающийся короткий подшипник скольжения при 
( смотририсунок 2)
|
|
|
– с длинными опорами, для которых центр опорного шарнира вследствие неравномерности распределения нагрузки по длине цапфы находится, как показано на рисунке 3. К таким опорам относятся сдвоенные несамоустанавливающиеся подшипники качения и удлиненные несамоустанавливающиеся подшипники скольжения при 
( смотри рисунок 3 ).
5) в зависимости от подвижности опор валы подразделяются:
– с шарнирно-неподвижными (фиксирующими) опорами.
К ним относятся подшипники, воспринимающие от вала одновременно радиальную и осевую нагрузки (рисунок 4);
– с шарнирно-подвижными (плавающими) опорами.
Такие опоры образуют подшипники, воспринимающие лишь радиальные нагрузки (рисунок 5).
6) по значению рабочей угловой скорости валы делятся на:
– тихоходные (валы барабанов вакуум-фильтров и так далее);
– быстроходные.
Расчет тихоходных валов заключается в расчете их на прочность и жесткость, а быстроходных – и на виброустойчивоть.
7) в зависимости от соотношения рабочей угловой скорости  и критической
и критической 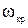 валы подразделяются на:
валы подразделяются на:
– жесткие при 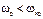 ;
;
– гибкие при 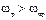 .
.
Один и тот же вал может быть и жестким и гибким в зависимости от выбранной угловой скорости вращения.

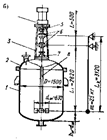


Рисунок 1 – Конструктивные и расчетные схемы валов
а – вал аппарата с одной сосредоточенной массой (мешалкой);
б – вал аппарата с двумя сосредоточенными массами (мешалками);
в – вал переменного поперечного сечения; г – однопролетный вал;
д – вал консольный.

Рисунок 2 – Короткие шарнирные опоры валов:
а – одиночный подшипник качения; б – сдвоенные подшипники качения, размещенные в сферической самоустанавливаюшейся втулке;
в – самоустанавливающийся подшипник скольжения.

Рисунок 3 – Длинные шарнирные опоры валов:
а – сдвоенные подшипники качения; б – несамоустанавливающийся подшипник скольжения.

Рисунок 4 – Некоторые конструктивные варианты шарнирно-неподвижных опор валов с подшипниками качения

Рисунок 5 – Некоторые конструктивные варианты шарнирно-подвижных опор валов с подшипниками качения
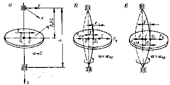
Рисунок 6 – Схемы положения центра инерции (точки С) диска, закрепленного в середине однопролетного вала:
а – не вращающегося ( 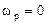 ); б и в – вращающегося с угловой скоростью
); б и в – вращающегося с угловой скоростью
 и
и  соответственно.
соответственно.
Классификация колебаний
Колебания могут быть классифицированы по различным признакам:
1) по физической природе различают:
– механические;
– электромагнитные;
– внутримолекулярные колебания.
Под механическими колебаниями понимают многократное поочередное возрастание и убывание во времени кинематических или динамических параметров, характеризующих механическую систему. Механические колебания могут проявлять себя как опасное явление, нарушающее режимы работы машины, что приводит к увеличению износа, повышению напряжений в деталях машин, вплоть до их разрушения, ухудшению условий труда (возрастанию уровня шума и вибрационного действия на человека и окружающую среду) и так далее. Источником механических колебаний многих машин является неуравновешенность их узлов и деталей.
2) в зависимости от причин, вызывающих колебания системы.
Они классифицируются следующим образом:
– свободные – колебания, которые совершаются при отсутствии внешнего воздействия и поступления энергии извне;
– вынужденные – колебания, вызванные внешним воздействием;
– параметрические колебания – определяются изменением во времени параметров системы. (Пример: колебание груза, закрепленного на горизонтальной наклонной балке при периодическом изменении длины консоли);
– автоколебания (самовозбуждающиеся колебания) – возникают и поддерживаются источником энергии неколебательной природы при условии, что источник энергии входит в рассматриваемую систему.
3) в зависимости от формы колеблющегося тела.
Различают колебания:
– материальных объектов, все три измерения которых сравнимы между собой. Таковы, например, фундаменты машин;
– оболочек (тонкостенных цилиндров, сфер и так далее) и тонкостенных пластин, то есть тел, два измерения которых значительны по сравнению с третьим (толщиной);
– стержней, то есть тел, в которых одно измерение (длина) весьма велико по сравнению с двумя другими.
Объектом изучения в настоящей работе являются валы, которые относятся к стержням, поэтому рассматриваются вопросы, связанные с расчетом этих деталей.
Различают три типа колебания стержней:
1) продольные колебания – сечения стержня колеблются вдоль оси стержня около положения равновесия;
2) поперечные колебания или колебания изгиба – сечения стержня смещаются нормально к его оси поочередно по одну и другую сторону от положения равновесия, поворачиваясь при этом вокруг своих нейтральных осей;
3) крутильные колебания – сечения стержня поворачиваются на некоторый угол φ, оставаясь в своей плоскости, вокруг оси стержня попеременно в одну и другую сторону.
Валы машин обычно совершают поперечные колебания, которые и будут в дальнейшем предметом изучения в данной работе.
Валы, классификация валов
1) в зависимости от количества установленных на валу деталей (дисков, шкивов, муфт, колес, мешалок и так далее). Различают валы
– с одной сосредоточенной массой;
– со многими сосредоточенными массами (рисунок 1, а;1, б).
При этом относительно менее массивные элементы полагают лишенными массы, а масса самого вала в зависимости от метода расчета может быть представлена либо в виде равномерно распределенной нагрузки, либо сосредоточенной распределенной между другими сосредоточенными массами. Масса вала может и не учитываться, если она составляет менее 30% массы детали вала (диска, барабана и так далее).
2) по виду поперечного сечения различаю валы:
– постоянного поперечного сечения;
– переменного поперечного сечения (рисунок 1, в).
3) в зависимости от места установки подшипников валы подразделяют на:
– однопролетные (рисунок 1, г);
– консольные (рисунок 1, д);
– многопролетные (неразрезные).
Расчет многопролетных валов принципиально ничем не отличается от расчета однопролетных валов, однако практически задача значительно и для машиностроения представляет ограниченный интерес.
4) по характеру опор (подшипников) различают валы:
– с короткими опорами, для которых центр опорного шарнира соответствует на расчетной схеме середине подшипника (рисунок 2 ).
К таким относятся одиночные подшипники качения, сдвоенный подшипник качения при условии самоустанавливаемости всего блока опоры, самоустанавливающийся подшипник скольжения при  и несамоустанавливающийся короткий подшипник скольжения при
и несамоустанавливающийся короткий подшипник скольжения при  ( смотририсунок 2)
( смотририсунок 2)
– с длинными опорами, для которых центр опорного шарнира вследствие неравномерности распределения нагрузки по длине цапфы находится, как показано на рисунке 3. К таким опорам относятся сдвоенные несамоустанавливающиеся подшипники качения и удлиненные несамоустанавливающиеся подшипники скольжения при 
( смотри рисунок 3 ).
5) в зависимости от подвижности опор валы подразделяются:
– с шарнирно-неподвижными (фиксирующими) опорами.
К ним относятся подшипники, воспринимающие от вала одновременно радиальную и осевую нагрузки (рисунок 4);
– с шарнирно-подвижными (плавающими) опорами.
Такие опоры образуют подшипники, воспринимающие лишь радиальные нагрузки (рисунок 5).
6) по значению рабочей угловой скорости валы делятся на:
– тихоходные (валы барабанов вакуум-фильтров и так далее);
– быстроходные.
Расчет тихоходных валов заключается в расчете их на прочность и жесткость, а быстроходных – и на виброустойчивоть.
7) в зависимости от соотношения рабочей угловой скорости  и критической
и критической 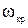 валы подразделяются на:
валы подразделяются на:
– жесткие при  ;
;
– гибкие при  .
.
Один и тот же вал может быть и жестким и гибким в зависимости от выбранной угловой скорости вращения.

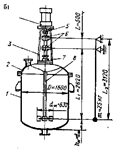
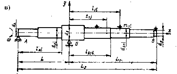

Рисунок 1 – Конструктивные и расчетные схемы валов
а – вал аппарата с одной сосредоточенной массой (мешалкой);
б – вал аппарата с двумя сосредоточенными массами (мешалками);
в – вал переменного поперечного сечения; г – однопролетный вал;
д – вал консольный.

Рисунок 2 – Короткие шарнирные опоры валов:
а – одиночный подшипник качения; б – сдвоенные подшипники качения, размещенные в сферической самоустанавливаюшейся втулке;
в – самоустанавливающийся подшипник скольжения.
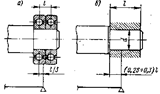
Рисунок 3 – Длинные шарнирные опоры валов:
а – сдвоенные подшипники качения; б – несамоустанавливающийся подшипник скольжения.

Рисунок 4 – Некоторые конструктивные варианты шарнирно-неподвижных опор валов с подшипниками качения
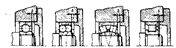
Рисунок 5 – Некоторые конструктивные варианты шарнирно-подвижных опор валов с подшипниками качения

Рисунок 6 – Схемы положения центра инерции (точки С) диска, закрепленного в середине однопролетного вала:
а – не вращающегося ( 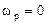 ); б и в – вращающегося с угловой скоростью
); б и в – вращающегося с угловой скоростью
 и
и  соответственно.
соответственно.
Дата добавления: 2019-11-25; просмотров: 298; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!

