Понятие о безмоментной (мембранной) и моментной теориях расчета уравнение Лапласа, уравнение зоны.
Понятие о безмоментной (мебранной) и моментной теориях расчета на прочность элементов аппаратов под действием внутреннего давленияслучае, когда вдоль меридиана не будет резких изменений внешней нагрузки, толщины оболочки и ее радиусов кривизны, то можно принять, что оболочка не подвергается изгибу, т.е. изгибающие моменты и поперечная сила равны нулю (Мx = Мy = Оy = 0), благодаря же симметрии формы и нагрузки оболочки действие крутящих моментов Мz и поперечной силы Оx на всех гранях исключено и тогда касательные напряжения отсутствуют.
Таким образом, по граням элемента действуют только нормальные усилия N; будем называть их соответственно меридиональными и обозначать N = U и тангенциальными (кольцевыми) N = Т От них возникают нормальные напряжения, соответственно - меридиональные sm и тангенциальные st .
От внутреннего газового давления возникают следующие внутренние силовые факторы: U–продольная меридиональная сила и T–кольцевое (тангенциальное) усилие, которые в любом поперечном сечении цилиндрической части корпуса колонны постоянны. От них возникают меридиональные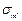 
и тангенциальные 
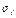напряжения, которые также не изменяются вдоль оси оболочки. На участках удаленных от узла сопряжения, данные напряжения определяются по известным формулам безмоментной теории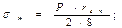 
(4.7)
В местах сопряжения оболочек различной толщины или оболочек, не имеющих общей касательной, возникают местные краевые изгибающие моменты
|
|
|
– меридиональный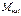 
и кольцевой (тангенциальный) 
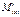, поперечная нагрузка 
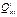, а также дополнительные растягивающие усилия –меридиональное 
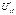и кольцевое (тангенциальное) 
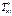, которые носят локальный характер, определяемый зоной действия краевого эффекта 
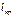. Данные параметры определяются в зависимости от величины 
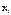–расстояние от края оболочки до 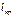. При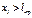 
влияние краевых нагрузок на ВСФ и напряжения существенно снижается и напряжения практически равны напряжениям, возникающим только от внутреннего давления.
При расчете оболочек по моментной теории цель расчета заключается в нахождении ВСФ, напряжений от совместного воздействия давления и краевых нагрузок 
(распорной силы) и проверке прочности узла сопряжения при толщине стенки, найденной только от внутреннего давления P.
Расчет на прочность по безмоментной теории: уравнение Лапласа, уравнение зоны
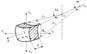
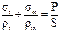уравнение Лапласа. Одного этого уравнения недостаточно для определения напряжений sm и st
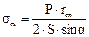уравнением зоны.
Из этого уравнения находится меридиональное напряжение sm.
Таким образом, по безмоментной теории напряжения sm и st в оболочке определяются из уравнений равновесия.
|
|
|
ОПРЕДЕЛЕНИЕ НАПРЯЖЕНИЙ ПО БЕЗМОМЕНТНОЙ ТЕОРИИ, ВОЗНИКАЮЩИХ В СТЕНКАХ ТОНКОСТЕННЫХ ОБОЛОЧЕК РАЗЛИЧНОЙ ФОРМЫ (ЦИЛИНДРИЧЕСКИХ, ЭЛЛИПТИЧЕСКИХ, СФЕРИЧЕСКИХ, КОНИЧЕСКИХ), НАХОДЯЩИХСЯ ПОД ВОЗДЕЙСТВИЕМ ВНУТРЕННЕГО ДАВЛЕНИЯ (ФОРМУЛЫ И СРАВНИТЕЛЬНЫЙ АНАЛИЗ).
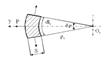
Для цилиндрической оболочки:
r t = R , r m = ¥ , α =0, со s 0=1
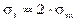
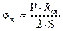
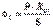
Определение напряжений и толщины стенки в цилиндрической оболочке
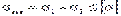
где sэкв – эквивалентное напряжение, МПа;
s1, s3 – главные напряжения, МПа, т.е. нормальные напряжения, действующие на площадках, где касательные напряжения (t) равны нулю;
[s] – допускаемое напряжение, МПа, которое определяется по справочным таблицам в зависимости от материала и расчетной температуры. Учитывая, что для цилиндрической оболочки , а из курса сопротивления материалов известно, что принимаем
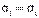
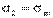
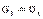
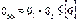
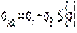
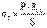
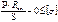
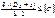
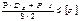
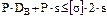
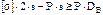
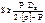
Расчет толщины стенки цилиндрической обечайки по ГОСТ
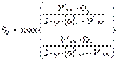
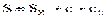
где SR – расчетная толщина стенки, мм;
S ц – исполнительная толщина стенки цилиндрической обечайки с учетом суммы прибавок, мм, определяемая по ГОСТ;
Р t рас , Рирас – расчетные давления соответственно в рабочих условиях и при испытаниях, МПа;
[ s ] t , [ s ] и 20 – допускаемые напряжения соовветственно в рабочих условиях и при испытаниях, МПа;
|
|
|
j – коэффициент прочности сварного шва. Учитывая, что прочность сварного шва может быть меньше, чем прочность основного металла, то уменьшают допускаемое напряжение на величину j, которая зависит от процента контролируемых швов; кроме этого, j зависит от вида сварного шва.
Определение толщины стенки и напряжений для оболочек конической формы
• - В эллиптической оболочке напряжения и радиусы кривизны в каждой отдельной точке на кривой (образующей эллиптического днища) различны. Они изменяются в зависимости от х и у и максимального своего значения достигают на полюсе.
• - H – глубина днища; R– радиус кривизны; Dв - внутренний диаметр
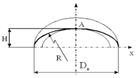
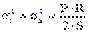
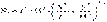
Толщина стенки эллиптической оболочки:
Дата добавления: 2019-11-25; просмотров: 369; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!