Напряжения, возникающие в элементах аппаратов (оболочках) различной формы (цилиндрических, эллиптических, сферичеких, конических) под действием внутреннего давления

Мембранная теория дает следующие значения напряжений для основных геометрических форм оболочек:

– сферический сосуд (шаровая оболочка, полушаровое днище) (рисунок 3.1.13), нагруженный равномерно распределенным внутренним давлением Р.

Для него r_t = r_m = R , где R – радиус сферы.

Рисунок 3.1.13 – Сферическая оболочка, нагруженная внутренним давлением

Тогда меридиональное напряжение s_m равно кольцевому напряжению s_t и они определяются по формуле

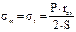, (3.1.19)

где r_сп – радиус срединной поверхности, м.

Рисунок 3.1.14 – Применение сферических оболочек для изготовления шаровых емкостей и полусферических днищ

– цилиндр с крышками, нагруженный равномерно распределенным давлением Р. (рисунок 3.1.15)

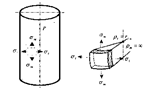
Рисунок 3.1.15 – Цилиндрическая обечайка Для него r_t = R, r_m =¥, тогда

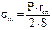,              (3.1.20)

,              (3.1.21)

при этом 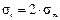,       (3.1.22)

то есть в продольных швах действуют в два раза большие напряжения, чем в поперечных (см. рисунок 3.1.11), и соответственно по этим швам в первую очередь может произойти разрыв при разрушении оболочки.

– конус, шарнирно подвешенный по краю со стороны основания, нагруженный равномерно распределенным давлением Р. Для него r_m = ¥. Кольцевые напряжения в любом сечении конического днища n - n можно найти из уравнения Лапласа. Учитывая, что величина

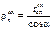,                          (3.23)

Получим ,                   (3.24)

где 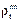,  – соответственно радиус кривизны и радиус конуса в сечении n – n. Величину меридиональных напряжений, возникающих в сечении n – n конуса можно определить из уравнения зоны (4), т.е

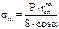.                        (3.25)

Из формул (3.1.24) и (3.1.25) вытекает, что максимальная величина кольцевых и меридиональных напряжений будет на краю конуса при r = R, причем

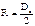,                              (3.26)

при этом кольцевые напряжения (как и для цилиндра) в любом данном сечении в 2 раза больше меридиональных, т.е.

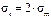.                          (3.27)

У вершины конуса при г = 0 и кольцевые и меридиональные напряжения равны нулю. Пример эпюры тангенциальных напряжений приведен на рисунке 3.1.16.

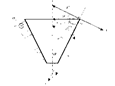
Риcунок 3.1.16 – Коническая оболочка, нагруженная внутренним давлением

Те же значения будут справедливы и для усеченного конуса, закрытого днищем. Эти формулы верны в том случае, если угол a< 80°, т.е. пригодны для расчета большинства конусов, являющимися частями аппаратов.

– в эллиптической оболочке напряжения и радиусы кривизны в каждой отдельной точке на кривой (образующей эллиптического днища) различны. Они изменяются в зависимости от х и у и максимального своего значения достигают в точке А (рисунок 3.7).

Максимальные напряжения определяются по следующим зависимостям

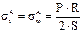,                  (3.28)

где R - радиус кривизны днища, м, который определяется по формуле

, (3.29)

где х и у – координаты заданной точки при условии, что начало координат находится а точке О; r – радиус днища, м.

В результате экспериментальных исследований было установлено, что оптимальной конструкции днищ соответствуют следующие параметры

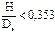.             (3.30)

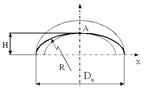
Рисунок 3.7 – Схема эллиптического днища

H – глубина днища; R– радиус кривизны; D_в - внутренний диаметр

Поэтому стали изготавливать стандартные эллиптические днища с отбортовкой на цилиндр высотой Н и параметрами 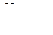 (рисунок 3.8).

 

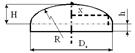
Рисунок 3.8 – Стандартное эллиптическое днище

 

Эллиптические днища одни из самых экономичных. Изготавливаются они штамповкой из листа из круглого проката (если диаметр листа равен диаметру днища, то без сварных швов), либо из сварных листов.

 

ПОНЯТИЕ О БЕЗМОМЕНТНОЙ (МЕМБРАННОЙ) И МОМЕНТНОЙ ТЕОРИЯХ РАСЧЕТА ТОНКОСТЕННЫХ ОБОЛОЧЕК, НАХОДЯЩИХСЯ ПОД ВОЗДЕЙСТВИЕМ ВНУТРЕННЕГО ДАВЛЕНИЯ. ВНУТРЕННИЕ СИЛОВЫЕ ФАКТОРЫ (ВНУТРЕННИЕ СИЛЫ) И НАПРЯЖЕНИЯ, ВОЗНИКАЮЩИЕ В ЭЛЕМЕНТЕ СТЕНКИ ОБОЛОЧКИ, ПРИ РАСЧЕТЕ ПО БЕЗМОМЕНТНОЙ И МОМЕНТНОЙ ТЕОРИЯХ.

В случае, когда вдоль меридиана не будет резких изменений внешней нагрузки, толщины оболочки и ее радиусов кривизны, то можно принять, что оболочка не подвергается изгибу, т.е. изгибающие моменты и поперечная сила равны нулю (М_x = М_y = О_y = 0), благодаря же симметрии формы и нагрузки оболочки действие крутящих моментов М_z и поперечной силы О_x на всех гранях исключено и тогда касательные напряжения отсутствуют.

Таким образом, по граням элемента действуют только нормальные усилия N; будем называть их соответственно меридиональными и обозначать N = U и тангенциальными (кольцевыми) N = Т От них возникают нормальные напряжения, соответственно - меридиональные s_m и тангенциальные s_{t .}

От внутреннего газового давления возникают следующие внутренние силовые факторы: U–продольная меридиональная сила и T–кольцевое (тангенциальное) усилие, которые в любом поперечном сечении цилиндрической части корпуса колонны постоянны. От них возникают меридиональные 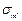 и тангенциальные  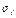напряжения, которые также не изменяются вдоль оси оболочки. На участках удаленных от узла сопряжения, данные напряжения определяются по известным формулам безмоментной теории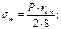

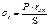
В местах сопряжения оболочек различной толщины или оболочек, не имеющих общей касательной, возникают местные краевые изгибающие моменты

– меридиональный 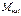 и кольцевой (тангенциальный)  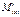, поперечная нагрузка 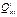, а также дополнительные растягивающие усилия –меридиональное  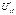и кольцевое (тангенциальное) 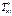, которые носят локальный характер, определяемый зоной действия краевого эффекта 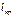. Данные параметры определяются в зависимости от величины  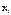–расстояние от края оболочки до 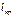. При 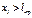влияние краевых нагрузок на ВСФ и напряжения существенно снижается и напряжения практически равны напряжениям, возникающим только от внутреннего давления.

При расчете оболочек по моментной теории цель расчета заключается в нахождении ВСФ, напряжений от совместного воздействия давления и краевых нагрузок 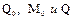 (распорной силы) и проверке прочности узла сопряжения при толщине стенки, найденной только от внутреннего давления P.

Для нахождения краевых нагрузок составляется расчетная схема узла сопряжения (рисунок 3). Нагрузки Q₀ и M₀ определяются из уравнений совместности деформаций. Учитывая, что в узле сопряжения деформации краев оболочек одинаковы, в общем виде можно записать:  

(1)

Это уравнение решается с использованием принципа независимости действия сил, то есть находятся деформации отдельно от каждой нагрузки и тогда уравнение переписывается в следующем виде 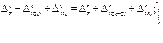    (2)

где 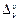, , 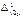, , 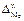,  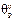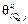– соответственно радиальные (м)

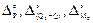и угловые (рад) деформации края цилиндрической обечайки под действием нагрузок Р, Q₀, М₀ ,  – соответственно радиальные (м) и угловые (рад) деформации эллиптической обечайки под действием нагрузок Р, Q₀, М₀.

При составлении данного уравнения применяется следующее правило знаков: линейные перемещения считаются положительными, если от рассматриваемой нагрузки край оболочки перемещается в направлении от оси.

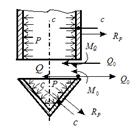
Рис. 3 – Расчетная схема для определения краевых нагрузок

Угловые перемещения считаются положительными, если внешняя нагрузка создаёт момент, направленный по часовой стрелке, относительно рассматриваемого сечения (например, сечение с – с, рисунок 3).

При этом в первом приближении принимается, что Q₀ >Q.

Для рассматриваемого случая уравнение (2) будет иметь следующий вид

Аналогично записывается уравнение для углов поворота, решаются два уравнения с двумя неизвестными и находятся значения Q₀ и M₀.

Определение распорной силы

В том случае, когда обечайки соединены под углом, т.е. не имеют общей касательной в узле сопряжения кроме краевых нагрузок Q₀ и M₀, возникает так называемая распорная сила Q, равномерно распределенная по краю.

     Как известно, в конической обечайке возникает продольная меридиональная сила U_x. Разложим ее на составляющие U^’_к и Q (рисунок 3.2.7).

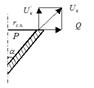 рисунок 3.2.7 – Схема разложения меридионального усилия на вертикальную и горизонтальную составляющие

 

При этом U^’_ц = U^’_к

где U^’_ц – меридиональная (продольная) сила, возникающая в цилиндрической обечайке под действием внутреннего давления.

Таким образом, и U^’_ц и U^’_к, взаимокомпенсируются, так как они направлены навстречу друг другу и равны между собой. В этом случае остается нескомпенсированной сила Q, так называемая распорная сила. Она как бы распирает обечайку, вызывая появление дополнительных деформаций и напряжений. Поэтому при конструировании конических днищ желательно, чтобы распорная сила была как можно меньше.

Распорная сила находится по следующей формуле .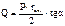

Таким образом, видно, что распорная сила зависит от внутреннего давления и геометрических параметров оболочки. Дополнительная краевая нагрузка – распорная сила Q может достигать очень больших значений, поэтому сопряжение обечаек под углом нежелательно и опасно.

---

Дата добавления: 2019-11-25; просмотров: 1833; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!