Расчет на прочность по безмоментной теории: уравнение Лапласа, уравнение зоны

Основным исходным уравнением безмоментной теории для расчета на прочность осесимметричных оболочек вращения, нагруженных внутренним избыточным давлением, является уравнение Лапласа.

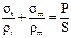уравнение Лапласа. Одного этого уравнения недостаточно для определения напряжений s_m и s_t

уравнением зоны.

Из этого уравнения находится меридиональное напряжение s_m.

Таким образом, по безмоментной теории напряжения s_m и s_t в оболочке определяются из уравнений равновесия.

Напряженное состояние материала стенки тонких оболочек. Понятие безмоментной и моментой теории расчета при воздействии внутреннего давления

При изучении основ безмоментной теории было доказано, что под действием внутреннего давления в стенках тонкостенных сосудов и аппаратов возникают:

- продольные растягивающие силы N,

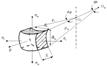
-изгибающие моменты M_m и M_t (рисунок 1 а),

-усилие от давления P

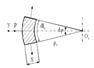
- поперечная сила Q_х (рисунок 1 б).

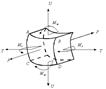
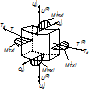
T, U–соответственно тангенциальные и меридиональные растягивающие усилия; M_t, M_m – тангенциальный и меридиональный изгибающий моменты; P – усилие от давления

Рисунок 1 – Внутренние силовые факторы, действующие на выделенный элемент оболочки

Однако, в случае, когда вдоль меридиана не будет резких изменений:

- внешней нагрузки,

- толщины оболочки и ее радиусов кривизны,

то можно принять, что оболочка не подвергается изгибу, т.е. изгибающие моменты и поперечная сила равны нулю (Мm = Мt = О_x = 0), благодаря же симметрии формы оболочки и нагрузки, действующей на нее, действие поперечной силы О_x на всех гранях исключено и тогда касательные напряжения отсутствуют.

Таким образом, по граням действуют только нормальные усилия N; будем называть их соответственно меридиональными и обозначать N = U (по меридиональным сечениям АВ и СД) и тангенциальными (кольцевыми) N = Т (по граням АС и ВД).

От них возникают нормальные напряжения, соответственно - меридиональные s_m и тангенциальные s_t (рисунок 2, 3).

Основанная на этих предположениях теория, не учитывающая действие изгибающих моментов, а принимающая во внимание только продольные силы U и Т, называетсябезмоментной илимембранной теорией расчета оболочек.

В этом случае, например, для цилиндрической оболочки напряжения определяются по следующим формулам

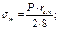
Однако в сосудах и аппаратах имеются такие узлы, по краям которых появляются так называемые краевые нагрузкиQ₀ , Q и M₀, от которых возникают дополнительные (т.е. дополнительно к U и T) внутренние силовые факторы (ВСФ):

- меридиональный (продольный) 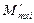 изгибающий момент (рисунок 1 б);

- кольцевой (тангенциальный, окружной) 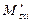 изгибающий момент,

- поперечная нагрузка ,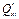

-растягивающие усилия – меридиональное 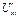 и кольцевое (тангенциальное)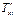

От этих дополнительных ВСФ возникают дополнительные напряжения, которые могут достигать значительных величин и ими нельзя пренебречь.

Такая теория расчета, при которой учитываются напряжения от этих дополнительных факторов, в том числе и от изгибающих моментов, называется моментной теорией. При этом напряжения называются краевыми и они могут достигать больших значений, поэтому необходимо уметь определять эти величины и принимать конструктивные меры для их снижения.

БЕЗМОМЕНТНАЯ ТЕОРИЯ РАСЧЕТА ТОНКИХ ОБОЛОЧЕК, НАХОДЯЩИХСЯ ПОД ВОЗДЕЙСТВИЕМ ВНУТРЕННЕГО ДАВЛЕНИЯ. УРАВНЕНИЕ ЛАПЛАСА, УРАВНЕНИЕ ЗОНЫ (ПРИВЕСТИ РИСУНКИ И ФОРМУЛЫ БЕЗ ВЫВОДА). С КАКОЙ ЦЕЛЬЮ СОСТАВЛЯЮТСЯ ДАННЫЕ УРАВНЕНИЯ?

 

При расчете оболочек вращения обычно определяют напряжения от действия внутреннего давления и толщину стенки. При этом рассматривают бесконечно малый элемент “D”, выделенный из оболочки двумя меридиональными и двумя кольцевыми сечениями

Как известно из курса сопротивления материалов, в самом общем случае от действия внешних нагрузок по каждой из граней могут действовать шесть внутренних силовых факторов (ВСФ):

– продольное (нормальное) усилие (сила) N_z;

– поперечные силы Q_x, Q_y;

– изгибающие M_x, M_y и крутящий M_zмоменты,от которых возникают нормальные s (от M_x, M_y, N_z) и касательные t (от Q_x, Q_y, M_z) напряжения.

Какие внутренние силовые факторы возникают в оболочке под действием внутреннего давления Р_внутр?

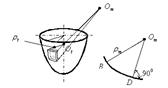
Для решения этой задачи рассмотрим пример – воздушный шарик, находящийся под действием газового давления.

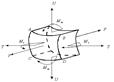
T, U– тангенциальные и меридиональные растягивающие усилия;

M_t, M_m – тангенциальный и меридиональный изгибающий моменты;

P – усилие от давления.

Изобразим деформации стенки сферы

Допустим, надули шарик до давления P₁ и он принял определенный размер, характеризующийся длиной окружности поперечного сечения.

Надуваем шарик до давления P₂> Р₁, размеры шарика увеличиваются и, соответственно, изменяются размеры дуги AB.

Из рисунка видно, что дуги не совпадут, так как, во-первых, одна дуга длиннее другой, т.е. на нее должны действовать растягивающие усилия, в данном случае тангенциальные – T , а во-вторых, различна их кривизна.

Изменить свою кривизну дуга может только под действием изгибающих моментов. Для рассматриваемого случая это – М_t.

Если шарик повернуть на 90°, то параллельный круг превратится в меридиан.

Для дуги BD будут происходить аналогичные изменения, т.е. на эту дугу будут действовать меридиональные растягивающие усилия U и меридиональный изгибающий момент M_m

Таким образом, в оболочках под действием внутреннего давления возникают усилия U и T и изгибающие моменты М_t, М_m.

Доказано, что в случае, когда вдоль меридиана не будет резких изменений внешней нагрузки, толщины оболочки и ее радиусов кривизны, то можно принять, что оболочка не подвергается изгибу, т.е. изгибающие моменты и поперечная сила равны нулю (М_x = М_y = О_y = 0), благодаря же симметрии формы и нагрузки оболочки действие крутящих моментов М_z и поперечной силы О_x на всех гранях исключено и тогда касательные напряжения отсутствуют.

Таким образом, по граням действуют только нормальные усилия N; будем называть их соответственно меридиональными и обозначать N = U и тангенциальными N = Т (по граням АС и ВД). От них возникают нормальные напряжения, соответственно - меридиональные s_m и тангенциальные s_t

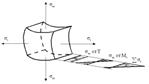
Кроме этого на грань АВСД действует внешняя нагрузка Р. (В данном примере это внутренне избыточное давление). От этой нагрузки возникает, так называемое, радиальное напряжение, направленное вдоль радиуса оболочки и равное по величине давлению, т. е. s_r = Р. для тонкостенных оболочек давление меньше 10 МПа, значительно меньше допускаемых напряжений, радиальные напряжения принимают равными нулю.

---

Дата добавления: 2019-11-25; просмотров: 553; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!