Напряженное состояние материала упругих осесимметричных оболочек вращения

При расчете оболочек вращения обычно определяют напряжения от действия внутреннего давления и толщину стенки. При этом рассматривают бесконечно малый элемент “D”, выделенный из оболочки двумя меридиональными и двумя кольцевыми сечениями (рисунок 3.1.6).

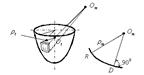
Рисунок 3.1.6 – Элемент оболочки

r_m – радиус кривизны меридиана; r_t – радиус кривизны параллельного круга.

Как известно из курса сопротивления материалов, в самом общем случае от действия внешних нагрузок по каждой из граней могут действовать шесть внутренних силовых факторов (ВСФ):

– продольное (нормальное) усилие (сила) N_z;

– поперечные силы Q_x, Q_y;

– изгибающие M_x, M_y и крутящийM_z моменты,

от которых возникают нормальные s (от M_x, M_y, N_z) и касательные t (от Q_x, Q_y, M_z) напряжения. На рисунке 3.1.7 показаны внутренние силовые факторы только по одному из сечений – меридиональному, аналогично можно было бы изобразить внутренние силовые факторы и по остальным трем граням.

Какие внутренние силовые факторы возникают в оболочке под действием внутреннего давления Р_внутр?

Для решения этой задачи рассмотрим пример – воздушный шарик, находящийся под действием газового давления.

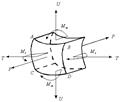
Рисунок 3.1.7 – Внутренние силовые факторы, действующие на выделенный

элемент оболочки

T, U– тангенциальные и меридиональные растягивающие усилия;

M_t, M_m – тангенциальный и меридиональный изгибающий моменты;

P – усилие от давления.

Изобразим деформации стенки сферы (рисунке 3.1.8).

Рисунок 3.1.8 – Деформации сферической оболочки

 

Допустим, надули шарик до давления P₁ и он принял определенный размер, характеризующийся длиной окружности поперечного сечения.

Надуваем шарик до давления P₂> Р₁, размеры шарика увеличиваются и, соответственно, изменяются размеры дуги AB.

Совместим эти дуги до деформации и после (рисунок 3.1.9).

Рисунок 3.1.9 – Схема совмещения дуг AB и A’B’

 

Из рисунка видно, что дуги не совпадут, так как, во-первых, одна дуга длиннее другой, т.е. на нее должны действовать растягивающие усилия, в данном случае тангенциальные – T , а во-вторых, различна их кривизна.

Изменить свою кривизну дуга может только под действием изгибающих моментов. Для рассматриваемого случая это – М_t.

Если шарик повернуть на 90°, то параллельный круг превратится в меридиан.

Для дуги BD будут происходить аналогичные изменения, т.е. на эту дугу будут действовать меридиональные растягивающие усилия U и меридиональный изгибающий момент M_m (рис.унок 3.1.10).

Таким образом, в оболочках под действием внутреннего давления возникают усилия U и T и изгибающие моменты М_t, М_m.

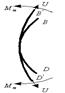
Рисунок 3.1.10 – Схема совмещения дуг BD и B’D’

 

Доказано, что в случае, когда вдоль меридиана не будет резких изменений внешней нагрузки, толщины оболочки и ее радиусов кривизны, то можно принять, что оболочка не подвергается изгибу, т.е. изгибающие моменты и поперечная сила равны нулю (М_x = М_y = О_y = 0), благодаря же симметрии формы и нагрузки оболочки действие крутящих моментов М_z и поперечной силы О_x на всех гранях исключено и тогда касательные напряжения отсутствуют.

Таким образом, по граням действуют только нормальные усилия N; будем называть их соответственно меридиональными и обозначать N = U (по меридиональным сечениям АВ и СД) и тангенциальными (кольцевыми) N = Т (по граням АС и ВД). От них возникают нормальные напряжения, соответственно - меридиональные s_m и тангенциальные s_t (рисунок 3.1.11).

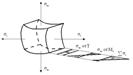
Рисунок 3.1.11 – Напряженное состояние и эпюры распределения тангенциальных напряжений по толщине стенки

Кроме этого на грань АВСД действует внешняя нагрузка Р. (В данном примере это внутренне избыточное давление). От этой нагрузки возникает, так называемое, радиальное напряжение, направленное вдоль радиуса оболочки и равное по величине давлению, т. е. s_r = Р. Так как для тонкостенных оболочек давление обычно меньше 10 МПа, то радиальное напряжение также не больше этого значения, и соответственно, значительно меньше допускаемых напряжений. Поэтому для тонкостенных оболочек обычно пренебрегают величиной радиальных напряжений и принимают их равными нулю.

При расчете тонкостенных оболочек считают, что кольцевые и меридиональные напряжения постоянны по толщине оболочки, т.е. пренебрегают их изменением (рисунок 3.1.11), как это наблюдается для толстостенных аппаратов.

Таким образом, можно принять, что напряженное состояние тонкостенных оболочек – плоское (двухосное).

Основанная на этих предположениях теория, не учитывающая действие изгибающих моментов, а принимающая во внимание только продольные силы U и Т, называетсябезмоментной илимембранной теорией расчета оболочек, в отличие отмоментной теории.

Тонкостенными называют цилиндрические аппараты, толщина стенки которых не превышает 10% внутреннего диаметра. Исходным уравнением для получения расчетной формулы при расчете на прочность тонкостенного цилиндра служит уравнение Лапласа безмоментной теории расчета тонкостенных оболочек, учитывающих только растягивающие напряжения. Строго говоря, под действием внутреннего давления стенка цилиндрической оболочки работает на растяжение и на изгиб. Так как в процессе деформации при переходе из положения ab в ab’’и далее в положение a’b’,элемент оболочки может удлиниться под действием расстягивающих усилий Т(переход из положения ab в a’b’) и изменить свою кривизну под действием изгибающих моментов К.

 

Растягивающее усилие Т в элементе длиной, равной единице, можно выразить через кольцевое напряжение, которое для цилиндра определяют уравнения Лапласа при ρ_k=Ρr/s’.

 

Эти напряжения вызовут относительное удлинение элемента ab на величину ε=σ_к/Е. Очевидно, радиус кривизны цилиндра увеличивается на величину _∆R= εR=pR²/Es’ и кривизна цилиндра изменится на величину 1/R-1/(R+Rε)= ε/R+ Rε.

Изгибающее напряжение, возникающее в стенке цилиндра под действием внутреннего давления, равно половине величины последнего.σ_{и=K/W=Ks’/I*2=p/2}

_{где W-момент сопротивления изгибу.}

 

Сопоставляя величины σ_ииσ_кможно увидеть, что значение σ_ипрактически мало по сравнению с величиной кольцевого напряжения σ_{к. В связи с этим} в подавляющем большинстве случаев изгибающие моменты в тонкостенных цилиндрах не учитывают и расчет ведут только на растягивающие напряжения по уравнению Лапласу.

Меридиональное напряжение в стенке цилиндра можно определить из условия равенства нагрузки на днище аппарата от внутреннего давления и усилия в кольцевом сечении стенки аппарата:Πr² p=2πRs’σ_m

Отсюда меридианльноенапржение σm=pR/2s’.для изготовления корпусов аппаратов, касательное напряжение, равное полуразности максимального и минимального напряжений, не должно превосходить половину допускаемого напряжения при одноосном растяжении

Из формул вытекает, что в цилиндрическом аппарате кольцевые напряжения σк в 2 раза больше меридиональных σm поэтому продольный шов и продольное сечение цилиндра являются более опасными. Согласно 3 теории прочности, удовлетворительной для сложного напряженного состояния таких относительно пластичных материалов, как стали, используемые для изготовления корпусов аппаратов, касательное напряжение, равное полуразности максимального и минимального напряжений , не должно превышать половину допускаемого напряжений при одноосном растяжении_.

В осесимметричных оболочках, находящихся под действием внутреннего давления Р, в самом общем случае в стенках аппаратов возникают тангенциальные σ_t, меридианальные σ_m, и радиальные σ_rнапряжения.

Для тонкостенных аппаратов  при расчете напряжений принимали, что:

- распределение тангенциальных (кольцевых) напряжений равномерно по толщине стенки;

- радиальным напряжением, максимальное значение которого не превышают 10 МПа, т.е. σ_r≤Р (т.к. для тонкостенных обычно Р< 10 МПа), можно пренебречь. В этом случае напряженное состояние материала оболочек – плоское (двухосное).

Для толстостенных оболочек нельзя принимать распределение σ_t по толщине стенки равномерным и пренебрегать радиальным напряжением, т.к. давление может достигать порядка 600 МПа и тогда σ_r =600МПа (на внутренних волокнах), что значительно больше допускаемых напряжений и соизмеримо с σ_t. В этом случае напряженное состояние материала оболочек - объемное (трехосное).

Таким образом, основными причинами, по которым аппараты подразделяются на тонко- и толстостенные являются:

1) отличие напряженных состояний материала оболочек:

- для тонкостенных – двухосное (σ_r ≈ 0; σ_m ≠ 0; σ_t ≠ 0);

- для толстостенных – объемное (σ_r ≠ 0; σ_m ≠ 0; σ_t ≠ 0);

2) различный характер распределения тангенциальных напряжений по толщине стенки:

- для тонкостенных - равномерное;

- для толстостенных - неравномерное.

Основными признаками деления сосудов на тонко- и толстостенные являются соотношение толщины стенки S к внутреннему диаметру D_в. и значение давлений, т.е.

- для тонкостенных:

а) (при D_в.>200мм) или ,

 

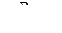где β - коэффициент толстостенности;

б) Р≤ 10 МПа (условное разделение);

- для толстостенных:

а) ,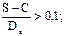

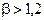б) Р> 10 МПа.

 

К аппаратам высокого давления.как было сказано ранее, относят аппараты, работающие под давлением свыше 10 МПа. Толщина стенки корпуса такого аппарата превышает 10 % его внутреннего диаметра, т.е. коэффициент толстостенности (отношение наружного диаметра к внутреннему)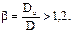

---

Дата добавления: 2019-11-25; просмотров: 317; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!