Гиперкомплексные числа малых размерностей. Часть 2

⇐ ПредыдущаяСтр 23 из 24Следующая ⇒

Рассмотренные нами комплексные, двойные и дуальные числа охватываются более общим понятием гиперкомплексной (сверхкомплексной) системы чисел. Мы изложим элементы теории таких чисел, следуя книге [13, § 5, 6] и слегка модифицируя обозначения с целью удобства дальнейшего изложения. Акцент будет сделан на процедурах удвоения гиперкомплексных чисел. При этом будет рассмотрена как стандартная процедура удвоения [13, c. 36], так и две нестандартные процедуры, определяемые нами в рамках данного проекта.

Ниже мы вновь используем «соглашение о вертикальной черте», которая отделяет учебную информацию от личных результатов исполнителей. Оно будет действовать на протяжении всего раздела 3.5.

3.5.1. Первоначальные сведения о гиперкомплексных числах и
нестандартные процедуры удвоения

Гиперкомплексным числом мы будет называть выражение вида 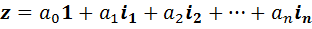, где 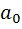, , 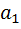…, 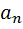– это произвольные вещественные числа, а , , 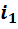… 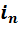– это некоторые символы (которые мы будем иногда называть «единицами»).

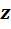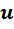Сложение и вычитание гиперкомплексных чисел определяется покомпонентно. Умножение гиперкомплексных чисел и определяется в несколько этапов.

1) Во-первых, считается, что 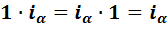при любом 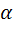от 1 до .

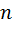2) Во-вторых, каждое слагаемое первой суммы умножается на каждое слагаемое второй суммы.

3) В-третьих, указывается, чему равно каждое из произведений вида 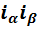, то есть задается система равенств

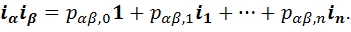(1)

4) В-четвертых, произведения 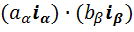переписываются в виде 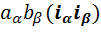, затем 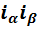заменяются по формуле (1) и, наконец, приводятся подобные члены. В итоге снова получается некоторое выражение вида (1).

Нетрудно доказать, что умножение гиперкомплексных чисел ассоциативно, дистрибутивно и однородно относительно умножения на вещественное число.

Каждое гиперкомплексное число 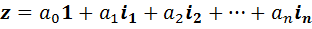порождает сопряженное ему гиперкомплексное число 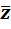, определяемое формулой .

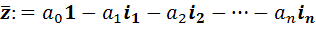Определение. Удвоением гиперкомплексной системы чисел 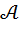называется новая гиперкомплексная система чисел 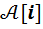, которая строится следующим образом.

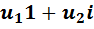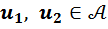1) Её элементы представляют собой выражения вида , где и .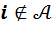

2) Сложение определяется покомпонентно.

3) Умножение определяется по формуле

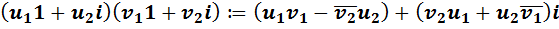. (У₁)

Нетрудно доказать, что умножение в удвоенной алгебре ассоциативно, дистрибутивно и однородно относительно умножения на вещественное число.

Добавим к описанной стандартной процедуре удвоения две нестандартные процедуры.

С помощью символа построим алгебру 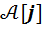, определяя сложение покомпонентно, а умножение по формуле

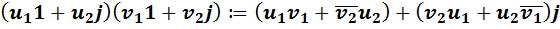. (У₂)

С помощью символа 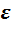построим алгебру 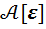, определяя сложение покомпонентно, а умножение по формуле

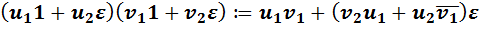. (У₃)

По формулам (У₁)–(У₃) нетрудно доказать, что 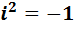, 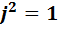и .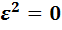

Отступим теперь от общих конструкций и вернёмся к «самому началу», то есть к алгебрам малых размерностей. Если учесть, что число, сопряжённое вещественному числу, равно ему самому, то мы сразу получаем следующие утверждения.

1) Алгебра комплексных чисел является удвоением алгебры вещественны чисел с помощью стандартной процедуры удвоения (У₁), то есть .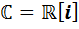

2) Алгебра двойных чисел является удвоением алгебры вещественны чисел с помощью первой нестандартной процедуры удвоения (У₂), то есть .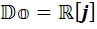

3) Алгебра дуальных чисел является удвоением алгебры вещественны чисел с помощью второй нестандартной процедуры удвоения (У₃), то есть .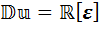

Если теперь ккаждой из трёх полученных алгебр применить каждую из трёх процедур удвоения, то получим девять алгебр. Перечислим их:

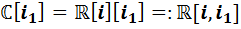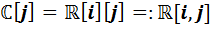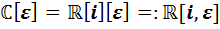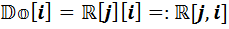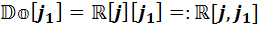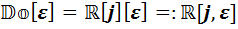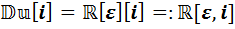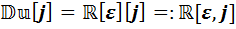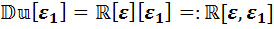В этих обозначениях встречаются индексы при одинаковых корневых буквах у мнимых единиц. Каждый раз это означает, что данные единицы являются разными, однако обладают общим характеристическим свойством. Так, в первом обозначении 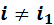, однако .

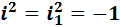Наличие девяти различных, но единообразно построенных, алгебр естественным образом порождает следующую задачу.

Задача. Выяснить, нет ли среди полученных девяти алгебр изоморфных друг другу. Если да, то найти все попарно изоморфные алгебры, доказав тем самым, что оставшиеся алгебры попарно не изоморфны.

3.5.2. Таблицы умножения для двукратных удвоений алгебры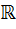

Очевидно, что никакое изучение алгебр невозможно до тех пор, пока не построены таблицы умножения. Школьники в начале проекта не имеют опыта построения таких таблиц, поэтому они нуждаются в образце, который будут использовать в дальнейшем. Такой образец даёт им руководитель, который подробно рассказывает о том, как строится таблица умножения для первой из алгебр 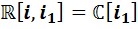. С точностью до обозначений мы получаем алгебру кватернионов, которая обладает целым рядом интересных свойств. 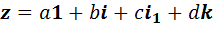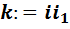Например, это некоммутативная, но ассоциативная алгебра с делением, элементы которой могут быть записаны в виде , где , а 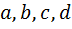– вещественные числа. При этом таблица умножения имеет вид

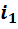
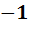
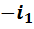
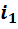
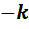
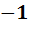
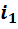
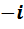
Теперь, когда образец предъявлен, школьники самостоятельно, но под контролем руководителя, строят таблицу умножения следующей из алгебр, а именно, алгебры 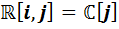. В некоторых источниках, например, в [24, с. 554], она называется алгеброй антикватернионов.

Опишем подробно процесс построения таблицы умножения.

Элемент 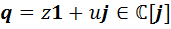может быть представлен в виде 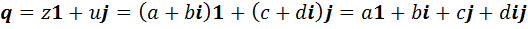. Если ввести обозначение 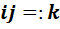, то 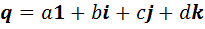. Составим таблицу умножения для элементов .

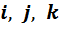Фактически, часть её уже составлена, поскольку 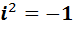, 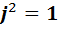и :

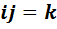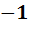
Продолжим заполнять пустые клетки таблицы, двигаясь последовательно по строкам слева направо.

1) Пользуясь ассоциативностью умножения и характеристическим свойством единицы , получим, что .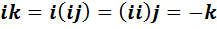

2) Пользуясь формулой (У₂) и определением единицы , получим, что

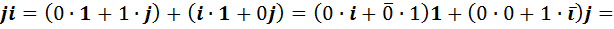
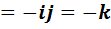В частности, мы получили полезное равенство 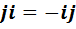, означающее антикоммутативность единиц и .

3) Используя определение единицы , последнее равенство, ассоциативность умножения и характеристическое свойство единицы , получим, что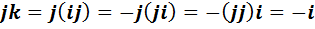

Если использовать все свойства, перечисленные в пунктах 1)–3), то нетрудно проделать вычисления, представленные в пунктах 4)–6).

4) .

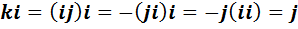5) .

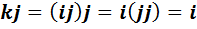6) .

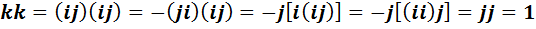Суммируя все результаты о попарных произведениях единиц, мы получаем следующую таблицу умножения:

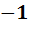
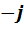
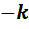
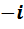
Теперь, когда школьники познакомились с образцом составления таблиц и самостоятельно составили одну из них, построение остальных семи таблиц становится вполне посильным и зависит только от их трудолюбия. Приведём перечень всех девяти таблиц умножения, полученных в результате двукратного удвоения алгебры вещественных чисел.

Перечень таблиц умножения

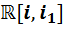
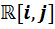
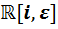
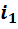
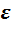
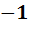
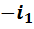
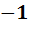
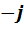
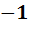
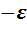
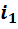
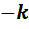
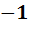
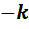
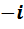
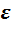
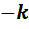
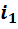
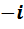
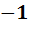
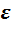
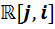
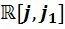
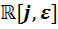
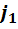
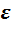
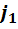
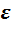
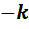
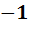
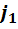
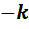
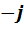
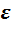
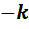
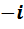
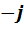
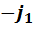
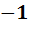
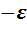
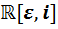
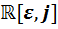
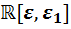
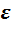
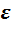
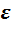
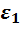
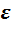
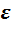
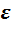
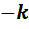
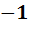
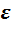
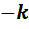
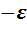
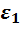
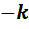
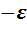
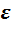
Бросается в глаза сходство полученных таблиц умножения. Во-первых, все они кососимметричны. Это означает, что элементы, стоящие на симметричных местах относительно главной диагонали, противоположны друг другу. Во-вторых, в каждой из них на главной диагонали стоят элементы , 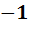и , присутствующие в том или ином количестве и расположенные в том или ином порядке. Естественно, что возникает потребность в объяснении причин сходства и в выявлении различий.

На уровне, если так можно выразиться, «гуманитарном» можно было бы предвидеть как сходство, так и различия алгебр. С одной стороны, все они получены единообразно, поэтому появление сходства у различных алгебр вполне естественно. С другой стороны, процедуры удвоения различны и при однократном удвоении приводят к разным результатам, поэтому появление различий у сходных алгебр также вполне естественно. Эти общие соображения нужно насытить математическим содержанием, что и будет сделано в следующем разделе.

3.5.3. Попарная изоморфность и неизоморфность
двукратных удвоений. Классификационный результат

В достаточной мере очевидно, что свойства алгебры зависят от того, каковы характеристические свойства мнимых единиц, образующих её базис. В таблице эти свойства отражаются на её главной диагонали, где содержатся квадраты этих единиц. Естественно предположить, что те алгебры, у которых диагонали таблиц отличаются только порядком элементов, окажутся изоморфными. Это предположение подтверждается следующей теоремой.

Теорема 1. Имеют место следующие изоморфизмы:

, , .

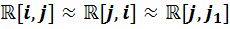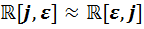Доказательство. Сначала изложим идею доказательства первого изоморфизма .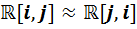

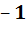Анализ таблиц умножения для двух алгебр показывает, что в обеих на главной диагонали находятся два элемента и один элемент , правда, на разных местах: в первой алгебре элемент 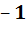стоит в начале диагонали, а во второй алгебре – в середине нее. Очевидно, что положение элемента 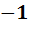на диагонали изменится, если поменять порядок базисных элементов , , , . Рассмотрим процесс изменения порядка более подробно.

Каждый элемент 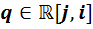имеет вид 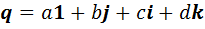. Его можно представить в другом виде: 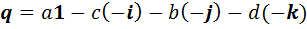. Введем новые обозначения следующим образом:

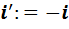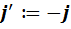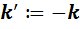, , . (2)

Теперь произвольный элемент алгебры приобретает вид 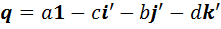. Другими словами, произвольный элемент 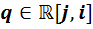разложен по новому базису, а именно, по базису , , , .

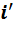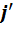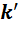Составим таблицу умножения для неединичных элементов нового базиса. При вычислении каждого из девяти произведений новой таблицы мы будем использовать одну и ту же последовательность действий: сначала используем обозначения (2), затем таблицу умножения в алгебре 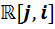, а затем вновь обозначения (2), если они потребуются.

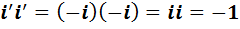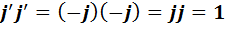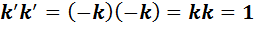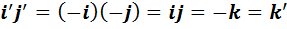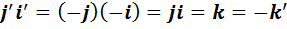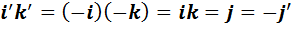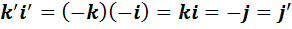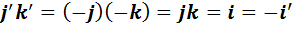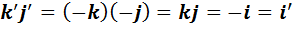Подставив результаты вычислений в искомую таблицу умножения, получим следующее:

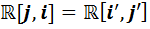
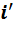
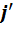
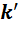
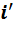
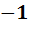
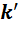
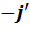
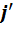
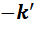
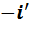
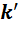
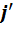
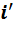
Если сравнить полученную таблицу умножения с таблицей умножения для 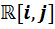, то мы увидим, что они различаются только обозначениями. Это и доказывает изоморфизм двух алгебр.

Остальные три изоморфизма доказываются аналогично.

При желании можно рассмотреть отображение 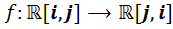, определяемое равенством 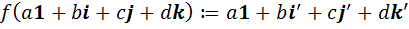, и прямой проверкой доказать, что оно является изоморфизмом.

Обозначения (2), рассматриваемые с геометрической точки зрения, означают, что при переходе от базиса , , , к базису , , 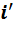, 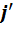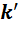мы заменили векторы , , на противоположные и изменили порядок следования двух векторов и .

Следствие. Если алгебру вещественных чисел удваивать с помощью одних и тех же единиц, вводящихся в различных порядках, то полученные алгебры окажутся изоморфными.

Доказательство сразу следует из первого, третьего и четвёртого изоморфизмов теоремы 1.

Если исключить из рассмотрения изоморфные экземпляры алгебр, то вместо девяти алгебр у нас останется только пять:

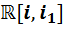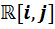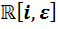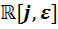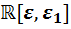, , , , . (3)

Относительно них справедливо следующее утверждение.

Теорема 2. Алгебры из списка (3) попарно не изоморфны.

Доказательство. Мы сделаем несколько однотипных шагов: рассмотрев какую-либо алгебру из списка (3), мы докажем, что она не изоморфна каждой из последующих алгебр списка. Начнём с первой алгебры.

Шаг 1. Алгебра 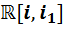не изоморфна каждой из четырех оставшихся алгебр , , , .

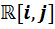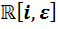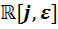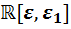1) Прежде всего, докажем, что 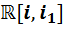является алгеброй с делением. Рассмотрим ненулевой элемент 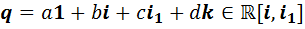и уравнение 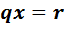. Домножив его справа на сопряженный элемент 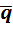, получим уравнение 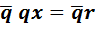. Произведя умножение взаимно сопряжённых элементов по таблице, получим, что 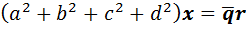. Поскольку коэффициент при 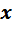отличен от нуля, мы можем поделить на него обе части уравнения и выразить 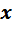. Рассуждая аналогично, мы можем решить уравнение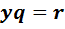

2) Докажем теперь, что каждая из четырёх оставшихся алгебр не является алгеброй с делением. Для этого достаточно показать, что в каждой из них существует делитель нуля. Напишем их: , , , .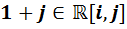

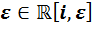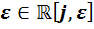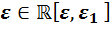3) Если теперь мы предположим, что алгебра 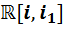изоморфна какой-либо из оставшихся алгебр, то предположение будет противоречить утверждениям пунктов 1) и 2)

Шаг 2. Алгебра 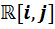не изоморфна каждой из трех оставшихся алгебр , , .

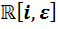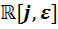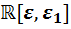1) Допустим, что 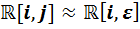. Во второй алгебре существует ненулевой элемент 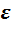, квадрат которого равен нулю, следовательно, в первой алгебре тоже должен существовать ненулевой элемент 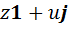, где 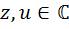, квадрат которого равен нулю: 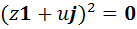. Вычислив левую часть по формуле (У₂), получим равенство 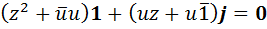, из которого следует система 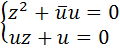. Из второго уравнения системы следует, что либо 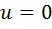, либо 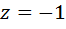. В обоих случаях мы придем к противоречию. Действительно, если 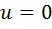, то из первого уравнения следует равенство 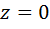, а это означает, что искомый ненулевой элемент оказался нулевым. Если 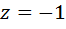, то из первого уравнения системы следует, что 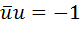. Это невозможно, потому что произведение двух взаимно сопряжённых комплексных является суммой квадратов вещественной части и мнимой части.

2) Если мы предположим наличие изоморфизмов 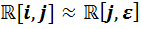или 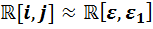, то мы можем дословно повторить рассуждение пункта 1) и прийти к противоречию.

Шаг 3. Алгебра 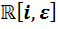не изоморфна каждой из двух оставшихся алгебр ,

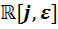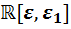
1) Допустим, что . В первой из алгебр существует ненулевой элемент , квадрат которого равен 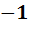, следовательно, во второй алгебре тоже должен существовать ненулевой элемент 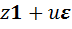, где 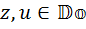, квадрат которого равен 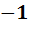, то есть должно выполняться равенство 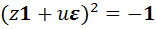. Вычислив левую часть по формуле (У₃), получим равенство 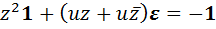, из которого следует система 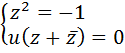. Первое из уравнений системы неразрешимо в области двойных чисел. Действительно, если 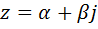, то из уравнения 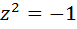следует, что 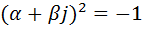, а отсюда вытекает равенство 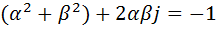. Следовательно, 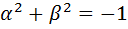, а это равенство противоречиво.

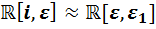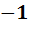2) Допустим, что . В первой из алгебр существует ненулевой элемент , квадрат которого равен , следовательно, во второй алгебре тоже должен существовать ненулевой элемент 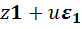, где 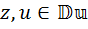, квадрат которого равен 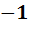, то есть должно выполняться равенство 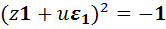. Вычислив левую часть по формуле (У₃), получим равенство 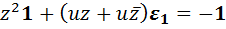, из которого следует система 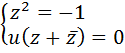. Первое из уравнений системы неразрешимо в области дуальных чисел. Действительно, если 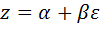, то из уравнения 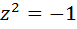следует, что 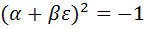, а отсюда вытекает равенство 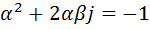. Следовательно, 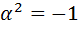, а это равенство противоречиво.

Шаг 4. Алгебры 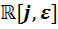и 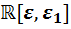не изоморфны друг другу.

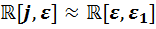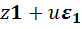Допустим, что . В первой из алгебр существует элемент , обладающий двумя свойствами: а) он не коллинеарен ; б) его квадрат равен . Следовательно, во второй алгебре тоже должен существовать элемент , где 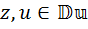, обладающий свойствами а) и б).

Начнём с уравнения 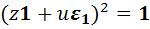. Вычислив левую часть по формуле (У₃), получим равенство 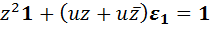, из которого следует система 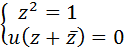. Пусть 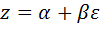. Тогда система примет вид 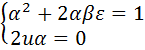, или в равносильной форме 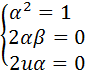. Из первого равенства системы следует, что 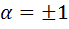, а из второго и третьего следует, что 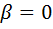и 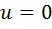. Окончательно получаем, что искомый элемент алгебры 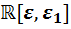имеет вид 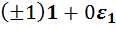. Этот элемент коллинеарен , то есть и не удовлетворяет свойству а). Тем самым мы пришли к противоречию.

Итак, теорема 2 доказана.

Наш общий вывод состоит в том, что теоремы 1 и 2 классифицируют алгебры, полученные с помощью двукратных удвоений алгебры вещественных чисел. Таким образом, мы самостоятельно получили ещё один полноценный классификационный результат.

Педагогическая рефлексия

Теперь, по завершении текста раздела, становятся понятны некоторые особенности проекта в целом. Кратко опишем их.

Первая особенность проекта состояла в том, что он имел большой объем. Именно поэтому он выполнялся в течение трёх лет, именно поэтому его выполняли два участника, именно поэтому он состоял из двух достаточно независимых частей. В этих условиях руководитель решал несколько задач, организационных и содержательных одновременно.

Во-первых, нужно было поддерживать интерес участников в течение длительного времени.

Во-вторых, нужно было распределить между участниками разные фрагменты вычислительной работы. При этом было весьма важно, чтобы каждый из участников не терял из виду общую стратегию исследования и был в курсе результатов товарища, более того, мог бы проверить его вычисления и в случае необходимости продолжить их.

В-третьих, распределение работ должно было быть продуктивным и, следовательно, справедливым. В условиях проекта это означало, что каждое задание каждому участнику должно было обладать двумя свойствами, конфликтующими друг с другом: с одной стороны, оно должно было быть посильным, а с другой стороны, требовать от участника практически всех его интеллектуальных ресурсов. Руководитель потратил много времени и использовал всю свою интуицию для составления разумных заданий. К сожалению (или к счастью), словесное описание такого рода работы недоступно ему.

В-четвертых, и это главное, необходимо было поддерживать в команде атмосферу научного исследования, которое приведёт к получению нового (или субъективно нового) результата.

Повторимся: автор не может описать, каким образом были решены сформулированные организационно-содержательные задачи, но они были решены, потому что проект был реализован.

Вторая особенность проекта связана с высокой абстрактностью тех объектов, которые были использованы в нем. Действительно, школьники 10-го и 11-го классов работали с алгебрами, с типологией алгебр, с изоморфизмами, гиперкомплексными системами и т.д. В этих условиях задача руководителя состояла в том, чтобы сделать эти понятия сначала знакомыми для школьников, потом привычными, потом не слишком трудными, потом интересными и т.д. Это было сделано в рамках обучающего компонента проекта. В нашем тексте этот компонент отражён с помощью вертикальной черты. К сожалению, обучающий компонент не мог быть представлен в полном объёме, однако мы надеемся, что читатель получил адекватное представление о нем.

Третья особенность проекта была связана с чрезвычайной, непривычной для школьников скрупулёзностью вычислительной работы. Действительно, приходилось представлять один и тот же элемент алгебры в разных формах, целесообразных для дальнейших рассуждений; выбирать одну из трёх процедур удвоения, именно ту, которая применима для дальнейших вычислений; находить произведения базисных векторов то по одной таблице, то по другой, каждый раз выбирая ту из них, которая имеет отношение к вычисляемому произведению… Поначалу руководителю приходилось исправлять большое количество ошибок, которые, конечно же, заводили в тупик. Постепенно количество ошибок уменьшалось и к концу проекта достигло уровня, естественного для математического исследования.

Четвертая особенность проекта была связана с личными свойствами научного руководителя. Дело в том, что в начале проекта руководитель не располагал той информацией, которая содержится в тексте книги. У него был некоторый (не очень большой) опыт работы в области алгебры, была убеждённость в своей способности решить поставленную им самим задачу, была надежда (впоследствии реализованная) увлечь школьников решением новой задачи, однако не было ни формулировок теорем, ни формулировок лемм, ни способов доказательства. Образно говоря, руководитель шёл «на две недели впереди» школьников. Разумеется, такая ситуация вполне могла закончиться крахом, поэтому она не может быть рекомендована читателю. Парадоксально, но именно опасность ситуации, а она не скрывалась от участников проекта, на определённом этапе поддерживала интерес школьников и придавала драйв нашей совместной работе.

Заключение

Швейцарские законы регламентируют использование удобрений на тех лугах, где пасутся коровы, из молока которых делают знаменитый швейцарский сыр. Этот пример показывает, насколько серьёзно относятся к своей деятельности тамошние сыроделы.

Если сравнить изготовление сыра с образованием школьника, ориентированного на исследовательскую деятельность, то становится понятным, что последнее должно быть длительным, многоэтапным и иметь весьма серьёзное теоретическое обоснование и методическое обеспечение. Конечно, обсуждаемые сущности настолько далеки друг от друга, что их сравнение может показаться некорректным, однако ясно, что изготовление высококачественного продукта требует длительной и тщательной предварительной подготовки. Именно поэтому автор и предлагает начинать исследовательски ориентированное обучение в младших классах и выдерживать эту линию до последних дней в школе. Именно поэтому автор и предлагает подчинить этой цели «все»: обычные уроки, внеурочную деятельность, экспериментальный и теоретический компоненты математики… Впрочем, и выигрыш для школьника может оказаться велик: знакомство с общенаучными методами исследования, приобщение к элементам деятельности математика и т.д.

Такой максимализм мог бы показаться чрезмерным, если бы не оказалось, что повседневная практика уже подготовила многое для реализации той концепции, которая изложена в книге. Действительно, содержание первой главы показывает, что существуют учебники для начальных классов, которые целенаправленно знакомят детей с общенаучными методами исследования. Содержание второй главы показывает, что традиционный материал может быть переработан в продуктивные сценарии преподавания и изучения математики, причём без чрезмерных усилий. Содержание третьей главы показывает, что многие научные задачи возникают буквально на страницах школьного учебника или дополнительной литературы того же уровня сложности.

Впрочем, энтузиазм уравновешивается некоторыми отрезвляющими вопросами, ответы на которые отнюдь не очевидны для автора. Ощущают ли учителя начальной школы, что они стоят в начале длительной работы по формированию школьника с менталитетом исследователя? Если да, то все хорошо, а если нет? Осознают ли учителя основной школы, что существенная часть пятиклассников неплохо подготовлена к решению интеллектуальных задач и, следовательно, необходимо развивать эту готовность? Станут ли они перерабатывать материал учебника в продуктивные сценарии, привлекая, если нужно, математические эксперименты? Очевидно, что какая-то часть учителей делает это, но насколько она велика, и задаёт ли она тон в жизни школьных коллективов? Видят ли учителя старших классов те научные задачи, которые могут быть сформулированы на материале школьных учебников? Будут ли они ставить перед отдельными старшеклассниками такие задачи или предпочтут готовить всех без исключения к единому государственному экзамену? Программы конференций школьников показывают, что многие учителя активно занимаются научным руководством своих учеников, однако, повторимся, задают ли они тон в жизни школьных коллективов?

Сказанное означает, что организация исследовательски ориентированного обучения вполне посильна как для сообщества учителей, так и для конкретных коллективов, хотя этот процесс является объективно сложным и психологически трудным. Можно сказать иначе: для решения сложной и трудной задачи – организации исследовательски ориентированного обучения – существует целый ряд педагогических инструментов и определённая традиция.

Обобщённо говоря, организация исследовательски ориентированного обучения математике является той задачей, которая лежит в «зоне ближайшего развития» математического и педагогического сообщества. Нам было бы целесообразно сделать усилие и перейти в новое качество.

Приложение

Дата добавления: 2019-09-13; просмотров: 342; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 15 16 17 18 19 20 21 222324 Следующая ⇒

Мы поможем в написании ваших работ!