Измерение расстояний, эквидистанты, равноудалённость

Обсудим несколько задач, которые естественным образом вытекают из всего вышеизложенного.

Задача 1. Опишите алгоритм нахождения расстояния от точки до каждой из фигур следующего списка: прямая, луч, отрезок, угол, окружность, треугольник, четырёхугольник.

Обсуждение. 1) Как уже было сказано, понятие расстояния от точки до прямой анализируется в учебнике. Поскольку любая наклонная к прямой длиннее перпендикуляра к ней, расстояние от точки до прямой равно длине отрезка перпендикуляра, проведённого из точки к прямой.

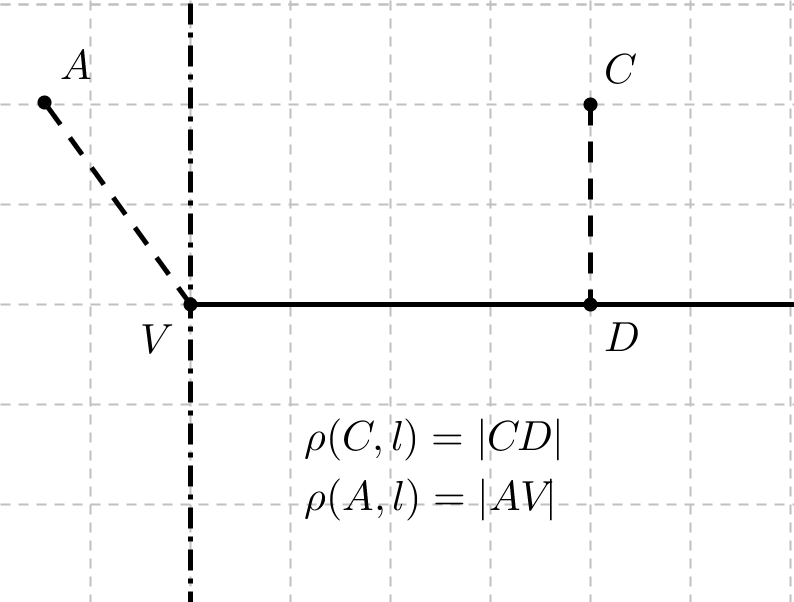Рис. 24. Расстояние от точки до луча

2) Алгоритм измерения расстояния от точки до луча с вершиной представлен на рис. 24. Приведём его словесное описание: «Через вершину луча проведем вспомогательную прямую, перпендикулярную ему. Эта прямая разделит плоскость на две полуплоскости, одна из которых содержит луч, а друга не содержит его. Если точка 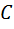содержится в первой полуплоскости, то расстояние от точки 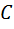до луча равно длине перпендикуляра, опущенного из точки 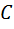на луч. Если точка 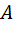содержится во второй полуплоскости, то расстояние от точки 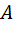до луча равно длине отрезка .»

Очевидно, что рис. 24 и текст в кавычках содержат одну и ту же информацию, закодированную разными способами. Если в процессе занятия сначала появляется рисунок, то текст в кавычках целесообразно рассматривать как алгоритмическое предписание, которое уточняет чертёж. Если же сначала появляется текст, то чертёж служит его визуализацией. По наблюдениям автора, школьникам существенно легче построить чертёж, чем составить объясняющий его текст. Это обстоятельство является хорошим поводом для того, чтобы продемонстрировать школьникам неразрывное единство математики и естественного языка, а также выявить взаимосвязь учебных дисциплин «математика» и «русский язык».

Заметим, кстати, что ни рис. 24, ни текст не объясняют, как измерить расстояние от точки до луча, если точка находится на штрих-пунктирной линии. Если это обстоятельство будет замечено школьниками, то возникнет хороший повод обсудить «неполноту» алгоритмического предписания, применимость обеих частей предписания в данном особом случае, принадлежность или непринадлежность границы полуплоскости самой полуплоскости и проч.

3) Очевидно, что для определения расстояния от точки до отрезка нужно провести две вспомогательные прямые, проходящие через его концы и перпендикулярные к нему. Они разобьют плоскость на три области, так что в процессе измерения расстояния возникнет «точка ветвления», в которой нужно будет выбрать один из трёх образов действия. Предлагаем читателю самостоятельно построить чертёж и сформировать поясняющий его текст.

4) Измеряя расстояние от точки до угла, треугольника и четырёхугольника, школьник вынужден комбинировать действия, описанные в пп. 2 и 3. Парадоксально, но мы можем сказать, что сложность измерения увеличивается и не увеличивается одновременно. С одной стороны, количество областей на плоскости увеличивается, а вместе с ним увеличивается количество действий по измерению расстояния. С другой стороны, каждое из этих действий уже было описано в пп. 2 или 3.

5) Измеряя расстояние от точки 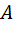до окружности с центром в точке 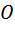, нужно построить луч , найти пересечение луча и окружности, а затем измерить расстояние .

Итак, решая задачу 1, школьник развивается, по крайней мере, в двух направлениях. Во-первых, он углубляется в суть понятия «расстояние» и может осмыслить школьные определения с новых позиций. Во-вторых, он видит, что при решении даже простой задачи приходится делать многочисленные дополнительные построения и конструировать их словесные описания. При этом конструирование словесных описаний оказываются отдельным, достаточно сложным литературным упражнением.

Теперь, когда мы умеем измерять расстояние от точки до различных геометрических фигур, мы можем сформулировать две новые задачи: о поиске эквидистанты и о поиске множества точек, равноудалённых от двух данных фигур.

Прежде всего, введём понятие эквидистанты. На первый взгляд, это понятие относится отнюдь не к школе, а к вузовскому курсу оснований геометрии, к тому его моменту, когда студентам рассказывают, что эквидистанта прямой в геометрии Лобачевского не является прямой. С другой стороны, нахождение эквидистанты геометрической фигуры является задачей вполне житейской. Действительно, по какой траектории должен двигаться катер, чтобы находиться на постоянном расстоянии от изрезанной береговой линии? (Этот академический вопрос может приобрести политическое звучание, если неизвестная эквидистанта является границей 200-мильной прибрежной зоны государства.)

Эквидистантой геометрической фигуры называется множество точек (геометрическое место точек, или ГМТ) плоскости, удалённых от данной фигуры на одинаковое расстояние.

Задача 2. Найдите эквидистанты каждой из следующих фигур: точка, прямая, луч, отрезок, угол, окружность, треугольник, четырёхугольник.

Обсуждение. Пусть каждая точка эквидистанты удалена от исходной геометрической фигуры на расстояние .

1) Очевидно, что эквидистантой точки является либо окружность радиуса при положительном , либо точка при .

2) Очевидно, что при положительном эквидистанта прямой представляет собой пару прямых, параллельных исходной прямой.

3) Эквидистанты луча и отрезка при положительном представлены на рис. 25 и 26.

Заслуживает внимания механическое истолкование эквидистанты отрезка. Её можно трактовать как траекторию точки, находящейся на ленте движущегося транспортёра, а также как форму гусеницы трактора. В связи с механической интерпретацией эквидистанты можно решать обратные задачи, например, такую: для какой геометрической фигуры её эквидистанта имеет форму велосипедной цепи?

4) Эквидистанта угла состоит из двух компонент связности (рис. 27). Одна из них находится внутри угла, а другая вне его. Первая представляет собой угол, конгруэнтный исходному, а вторая – «угол со сглаженной вершиной». Мы вновь сталкиваемся с ситуа-

Рис. 25. Эквидистанта луча

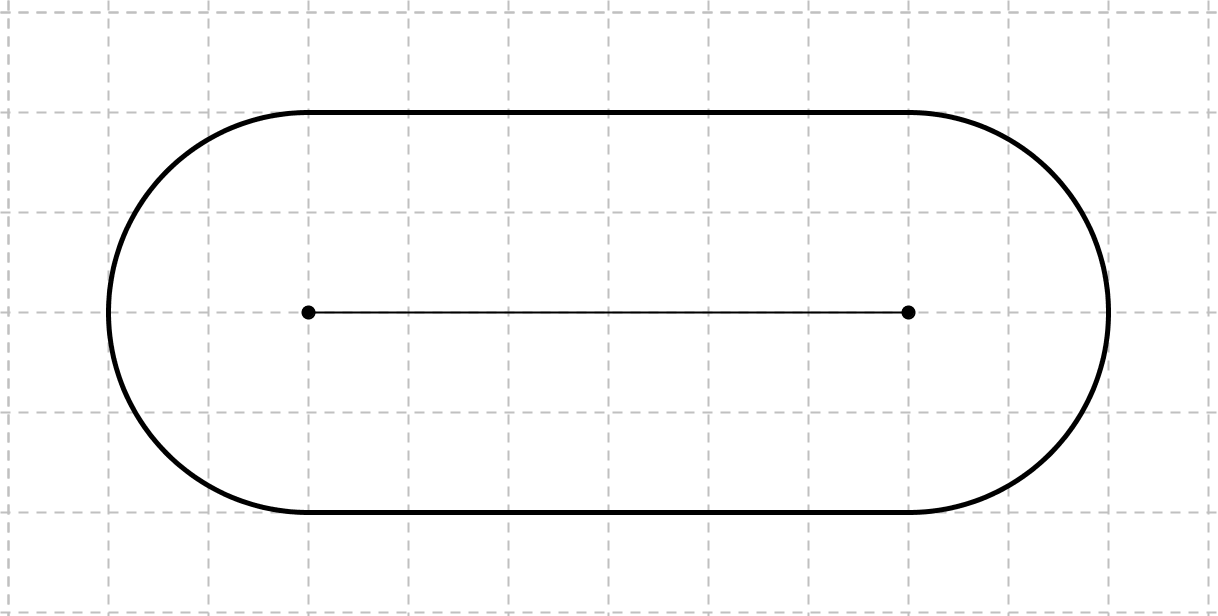Рис. 26. Эквидистанта отрезка

цией, в которой отнюдь не просто дать словесное описание чертежа, понятного с математической точки зрения. Именно нетривиальность такого литературного упражнения в сочетании с его доступностью (математика понятна!) делает это упражнение полезным для школьников.

5) Форма эквидистанты окружности радиуса зависит от соотношения между и . Если , то эквидистанта состоит из двух концентрических окружностей (рис. 28), одна из которых содержится вне круга, а другая внутри него. С ростом r радиус

внешней окружности растёт, а внутренней уменьшается. При достижении равенства внутренняя окружность вырождается в точку (центр исходной окружности), а при внутри исходного круга не остаётся точек эквидистанты.

6) Форма эквидистанты треугольника состоит из двух компонент и зависит от величины . Компонента эквидистанты, внешняя по отношению к треугольнику, представляет собой «треугольник со

Рис. 27. Эквидистанта угла

Рис. 28. Эквидистанта окружности

сглаженными вершинами», подобно тому, как это имеет место для угла. Внутренняя компонента эквидистанты при «малых» является треугольником, который гомотетичен исходному. При этом центром гомотетии является точка пересечения биссектрис. По мере роста внутренняя компонента эквидистанты сначала уменьшается, затем вырождается в точку (центр вписанной окружности), а затем исчезает. Полезным упражнением для школьника является построения соответствующих чертежей на бумаге или построение динамического чертежа в интерактивной математической среде.

7) Для четырёхугольника вид внутренней компоненты эквидистанты зависит не только от величины , но и от вида исходного четырёхугольника. С ростом внутренняя компонента эквидистанты преобразуется по одной из следующих схем:

Четырёхугольник Треугольник Точка Пустое множество,

Четырёхугольник Отрезок Пустое множество.

Повторимся: для школьника весьма полезно разобраться во всех хитросплетениях между величиной , формой исходного четырёхугольника и типом вырождения эквидистанты.

Мы видим, что в процессе решения задачи 2 продолжается развитие школьника. Прежде всего, он применяет обобщённое понятие расстояния в конкретных ситуациях. Кроме того, он знакомится с такими понятиями, как эквидистанта, компонента связности, вырождение фигуры. Наконец, он подходит к необходимости строить динамические чертежи, зависящие от одного параметра – расстояния.

Следующая задача проекта в буквальном смысле рождается на страницах школьного учебника. Действительно, в нем содержится теорема о геометрическом месте точке, равноудалённых от концов отрезка, а также теорема о геометрическом месте точек, равноудалённых от сторон угла и лежащих внутри него. В обоих случаях можно сказать, что рассматривается множество точек, равноудалённых от двух геометрических фигур: точки и точки в первом случае и луча и луча во втором случае. На этом фоне естественно рассмотреть следующее обобщение.

Задача 3. Найдите множество точек плоскости, равноудалённых от двух геометрических фигур, если фигуры выбраны из следующего списка: точка, прямая, луч, окружность.

Обсуждение. Решение данной задачи имеет ряд особенностей. Первая из них состоит в том, что школьник сталкивается с необходимостью достаточно детального планирования своего исследования. Первый этап планирования происходит ещё до того, как начинаются какие бы то ни было математические действия.

Во-первых, из списка фигур, предложенного в задаче, можно образовать 10 неупорядоченных пар фигур в соответствии с нижеследующей таблицей.

	Точка	Прямая	Луч	Окружность
Точка	1	2	3	4
Прямая		5	6	7
Луч			8	9
Окружность				10

Таким образом, оказывается, что предстоит изучить 10 ситуаций, никак не связанных или слабо связанных друг с другом.

Во-вторых, многие из этих ситуаций требуют дальнейшего планирования своих действий. Например, в случае 10, когда выбраны две окружности и радиусов и соответственно, необходимо рассмотреть ряд особенностей в соответствии со следующим меню.

Радиусы различны.

1.1. Окружности и соответствующие круги не имеют общих точек.

1.2. Окружности касаются внешним образом.

1.3. Окружности пересекаются в двух точках.

1.4. Окружности касаются внутренним образом.

1.5. Одна из окружностей лежит внутри круга, ограниченного

другой окружностью.

Радиусы равны.

2.1. Окружности и соответствующие круги не имеют общих точек.

2.2. Окружности касаются внешним образом.

2.3. Окружности пересекаются в двух точках.

2.4. Окружности совпадают.

Таким образом, ситуация 10 распадается, в свою очередь, ещё на 9 случаев.

В-третьих, и это парадоксально, планирование как таковое в некоторых случаях захлёбывается и должно перемежаться с исследованием тех случаев, которые удаётся выделить к данному моменту. Такова, например, ситуация 8, в которой изучается множество точек, равноудалённых от двух лучей. Действительно, два луча могут быть коллинеарны или разнонаправлены. Коллинеарные лучи могут быть сонаправлены или противонаправлены. Противонаправленные лучи могут лежать на разных прямых или на одной прямой. Противонаправленные лучи, лежащие на одной прямой, могут пересекаться или не пересекаться... Очевидно, что для полного исследования придётся составить многоуровневое меню, которое трудно сконструировать на момент начала решения.

Рис. 29. Равноудалённость от сторон угла

Вторая особенность исследования состоит в том, что промежуточные результаты оказываются непредсказуемыми, причём даже в тех случаях, которые кажутся знакомыми. Рассмотрим, например, множество точек, равноудалённых от двух разнонаправленных лучей с общей вершиной. На первый взгляд, множеством точек, равноудалённых от сторон угла, является его биссектриса. Это действительно так, если иметь в виду только точки, лежащие внутри угла. Если же искать равноудалённые точки на всей плоскости, то в процессе измерения расстояния от точки до луча придётся рассуждать так же, как в п. 1 обсуждения задачи 1. В результате к биссектрисе придётся добавить заштрихованную часть плоскости (рис. 29), ограниченную лучами, перпендикулярными двум исходным лучам.

Третья особенность исследования (неожиданная даже для автора как научного руководителя) состоит в том, что в качестве искомых множеств появляются кривые второго порядка во всем их многообразии. С ними мы сталкиваемся в самом начале исследования при изучении ситуации 2 из таблицы, когда разыскивается множество точек, равноудалённых от точки и прямой. Согласно определению [2, гл. IV] это парабола. Здесь самое время познакомить школьника с вузовским учебником по аналитической геометрии, вывести уравнение параболы или изучить его вывод по учебнику, и вообще предпринять какие-либо действия, расширяющиеся кругозор школьника и адекватные педагогической ситуации.

Рис. 30. Равноудалённость от непересающихся окружностей

Парабола не является единственным примером. Перейдём к ситуации 10, в которой изучается множество точек плоскости, равноудалённых от двух окружностей. Рассмотрим, например, окружности из пункта 1.1 меню, то есть окружности разных радиусов, у которых соответствующие замкнутые круги не имеют общих точек (рис.30).

Пусть – произвольная точка искомого множества. Вид этого множества можно получить, если рассмотреть следующую цепочку эквиваленций:

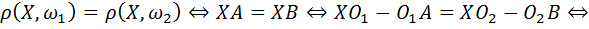
Последнее утверждение этой цепочки означает, что разность расстояний от произвольной точки до двух фиксированных точек и есть величина постоянная. Согласно определению [2, гл. IV] это гипербола (точнее, одна из её ветвей) с фокусами и .

В качестве другого примера рассмотрим окружности из пункта 1.3 меню, то есть окружности разных радиусов, пересекающиеся в двух точках (рис. 31). Пусть – произвольная точка искомого мно-

Рис. 31. Равноудалённость от пересекающихся окружностей-1

жества, лежащая в объединении кругов, но не лежащая в их пересечении. Вид этого множества можно получить, если рассмотреть следующую цепочку эквиваленций:

Последнее утверждение этой цепочки означает, что сумма расстояний от произвольной точки до двух фиксированных точек и есть величина постоянная. Согласно определению [2, гл. IV] это эллипс с фокусами и .

Итак, три основные кривые второго порядка мы получили единообразным способом как множества точек, равноудалённых от двух геометрических фигур. Распавшиеся кривые второго порядка могут быть получены тем же способом.

Здесь естественным образом возникает ситуация, которая требует от школьника выхода за границы имеющихся у него знаний и рассмотрения ситуации с некоей более высокой точки зрения. Для этого нужно просто продолжить исследование двух пересекающихся окружностей и найти точки из пересечения кругов, которые равноудалены от окружностей (рис. 32). Пусть – произвольная точка искомого множества. Вид этого множества можно получить, если

Рис. 32. Равноудалённость от пересекающихся окружностей-2

рассмотреть следующую цепочку эквиваленций:

Вновь мы видим, что искомые точки лежат на гиперболе с фокусами и . Если искать равноудаленные точки вне объединения кругов, то мы придём к той же гиперболе.

Окончательно мы получаем, что искомое множество является объединением эллипса и гиперболы.

Здесь возникает «точка роста» для школьника-математика, проходя которую он существенно расширяет границы своих предыдущих знаний. Действительно, он узнал, что эллипс и гипербола задаются уравнениями и соответственно, в силу чего являются кривыми второго порядка. А далее нужно использовать школьные знания! Поскольку искомое множество является объединением кривых, то оно должно задаваться либо совокупностью двух предыдущих уравнений, либо единым уравнением . Последнее уравнение и означает, что искомое множество является кривой четвертого порядка, более точно, распавшейся кривой.

Педагогическая рефлексия

Очевидно, что в любом проекте существуют барьеры, без преодоления которых возникновение и/или дальнейшее развитие проекта невозможно. В нашем случае таким барьером является работа научного руководителя, осуществляемая им до начала проекта. Действительно, руководитель должен проанализировать содержание школьного учебника с более высоких, чем обычно, математических позиций, должен понять, что понятие расстояния от точки до сложной геометрической фигуры вполне доступно для школьника, должен придумать методику введения общего определения… Кратко говоря, руководитель должен проделать целый ряд неформализуемых действий, направленных на постановку математической задачи для школьника.

Школьник – исполнитель проекта – вольно или невольно существенно расширяет свой математический арсенал. Даже если говорить только о понятиях, то он знакомится с обобщением понятия расстояния, с обобщением понятия равноудалённости, с определением эквидистанты, с представлением о вырождении геометрической фигуры, с представлением о кривых различных порядков. Однако более важным, с нашей точки зрения, является процесс приобретения навыков научной деятельности: участие в постановке задач, планирование своей работы, скрупулёзная проработка пунктов плана, получение вышеупомянутых обобщений… Разумеется, на уровне школы процесс приобретения навыков научной деятельности находится в самом начале, однако ситуация начала неизбежна, а научная задача, рождённая на страницах учебника, чрезвычайно полезна для интеллектуального развития школьника.

Дата добавления: 2019-09-13; просмотров: 514; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 12 13 14 15 161718 19 20 21 Следующая ⇒

Мы поможем в написании ваших работ!