Числовая мера разносторонности треугольника
Настоящий проект имеет несколько особенностей, которые могут показаться интересными. Во-первых, математическая задача основана на чрезвычайно простых соображениях и не требует для своей формулировки практически никакой предварительной подготовки. Во-вторых, основная идея решения возникает в результате компьютерного эксперимента, необходимость которого отнюдь не вытекает из формулировки задачи и целесообразность которого, вообще говоря, не очевидна. В-третьих, оттолкнувшись от эксперимента, исследование школьника течет в сугубо теоретическом русле [41].
Постановка задачи
Представим себе, что на вертикальной стене нарисован равнобедренный треугольник  с горизонтальным основанием
с горизонтальным основанием  длиною 1 м и вертикальной высотой
длиною 1 м и вертикальной высотой  длиною 1,5 м.
длиною 1,5 м.
Будем смещать вершину 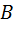 параллельно основанию. Более точно, рассмотрим три её положения: 1)
параллельно основанию. Более точно, рассмотрим три её положения: 1) 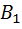 , где
, где 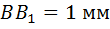 ; 2)
; 2) 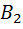 , где
, где 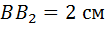 ; 3)
; 3)  , где
, где 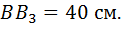 Нарисуем треугольники
Нарисуем треугольники 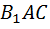 ,
,  и
и 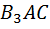 , а боковые стороны исходного треугольника сотрем.
, а боковые стороны исходного треугольника сотрем.
Можно с уверенностью сказать, что человек со стандартным глазомером сочтёт разносторонний треугольник 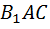 равнобедренным. Возможно, он не заметит разносторонность треугольника
равнобедренным. Возможно, он не заметит разносторонность треугольника  . Если же подозрения в разносторонности возникнут, то их можно будет легко подтвердить, найдя с помощью отвеса высоту
. Если же подозрения в разносторонности возникнут, то их можно будет легко подтвердить, найдя с помощью отвеса высоту 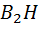 и убедившись с помощью нити того же отвеса, что
и убедившись с помощью нити того же отвеса, что 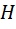 не является серединой стороны
не является серединой стороны  . Что же касается треугольника
. Что же касается треугольника 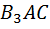 , то он изначально будет восприниматься как разносторонний и не будет находиться в ассоциативной связи с каким бы то ни было равнобедренным треугольником.
, то он изначально будет восприниматься как разносторонний и не будет находиться в ассоциативной связи с каким бы то ни было равнобедренным треугольником.
|
|
|
Обобщённо говоря, на интуитивном уровне человек ощущает, что три разносторонних треугольника 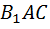 ,
,  и
и 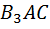 являются разносторонними как-то «по-разному», что они имею различные «количества разносторонности».
являются разносторонними как-то «по-разному», что они имею различные «количества разносторонности».
Слова в кавычках, будучи интуитивно понятными, не обладают точным математическим смыслом. Так возникает математическая
Задача 1. Ввести числовую меру разносторонности треугольника и изучить её свойства.
Наблюдение и основное определение
Один из подходов к решению задачи подсказывает наблюдение за динамическим чертежом, который можно создать в какой-либо интерактивной математической среде, например, в GeoGebra.
Изобразим равнобедренный треугольник 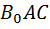 и отметим середину
и отметим середину 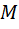 его основания
его основания  (рис. 33).
(рис. 33).
Через точку 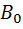 проведем прямую
проведем прямую  , параллельную основанию, и отметим на ней точку
, параллельную основанию, и отметим на ней точку 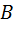 . Построим треугольник
. Построим треугольник  , проведем биссектрису
, проведем биссектрису  угла
угла 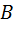 и совместим точку
и совместим точку 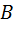 с точкой
с точкой 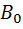 . Двигая точку
. Двигая точку 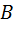 вдоль прямой
вдоль прямой  (скажем, «направо»), будем наблюдать за движением точки
(скажем, «направо»), будем наблюдать за движением точки 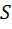 .
.
Очевидно, что в исходный момент времени точка 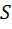 будет совпадать с точкой
будет совпадать с точкой 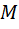 . В начале движения точки
. В начале движения точки 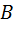 точка
точка 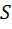 будет удаляться от точки
будет удаляться от точки 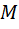 , а затем начнет приближаться к ней. По мере удаления точки
, а затем начнет приближаться к ней. По мере удаления точки 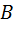 «в бесконечность» точка
«в бесконечность» точка 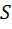 будет неограниченно
будет неограниченно
|
|
|

Рис. 33. Как движется основание биссектрисы?
приближаться к точке 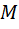 , но никогда не будет совпадать с ней.
, но никогда не будет совпадать с ней.
Дадим геометрическое истолкование наблюдаемым физическим явлениям.
В самом начале движения длина отрезка 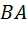 увеличивается, а длина отрезка
увеличивается, а длина отрезка  уменьшается. Следовательно, отношение
уменьшается. Следовательно, отношение 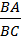 возрастает, а значит, возрастает и равное ему отношение
возрастает, а значит, возрастает и равное ему отношение 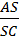 . В силу возрастания этого последнего отношения происходит удаление точки
. В силу возрастания этого последнего отношения происходит удаление точки 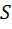 от точки
от точки 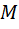 . Образно говоря, треугольник
. Образно говоря, треугольник  становится все менее и менее «похож» на равнобедренный.
становится все менее и менее «похож» на равнобедренный.
По мере того, как точка 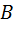 уходит все дальше и дальше, начинает превалировать другой фактор. Очевидно, что самая длинная сторона
уходит все дальше и дальше, начинает превалировать другой фактор. Очевидно, что самая длинная сторона 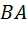 удовлетворяет неравенству
удовлетворяет неравенству 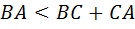 , откуда следует, что
, откуда следует, что 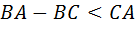 и
и 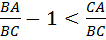 . В процессе движения точки
. В процессе движения точки 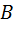 длина стороны
длина стороны 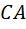 остается постоянной, а длина стороны
остается постоянной, а длина стороны  стремится к бесконечности, откуда следует, что
стремится к бесконечности, откуда следует, что 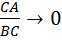 и
и 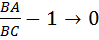 , а значит,
, а значит, 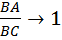 . Образно говоря, последнее соотношение можно истолковать так: треугольник
. Образно говоря, последнее соотношение можно истолковать так: треугольник  становится все более и более «похож» на равнобедренный треугольник с «почти равными» сторонами
становится все более и более «похож» на равнобедренный треугольник с «почти равными» сторонами 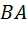 и
и  .
.
|
|
|
Итак, сделанное наблюдение показывает, что сходство или несходство треугольника  с равнобедренным связано с величиной расстояния
с равнобедренным связано с величиной расстояния 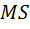 между основаниями медианы и биссектрисы.
между основаниями медианы и биссектрисы.
Дадим теперь точные определения.
Определение 1. Медианно-биссектральной частью стороны треугольника называется отрезок, концами которого являются основания медианы и биссектрисы, проведённые к этой стороне.
Для краткости будем называть их mb-частью или mb-отрезком стороны треугольника.
Определение 2. Индексом разносторонности угла 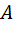 называется число, равное отношению длины mb-части противоположной стороны к этой стороне.
называется число, равное отношению длины mb-части противоположной стороны к этой стороне.
Отметим одно неочевидное обстоятельство: определение индекса разносторонности угла похоже на определение давления в физике. Действительно, давление 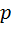 , производимое силой
, производимое силой  на фигуру площади
на фигуру площади 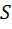 , измеряется по формуле
, измеряется по формуле 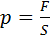 , то есть представляет собой силу, приходящуюся на единицу площади. Подобно этому, индекс разносторонности представляет собой ту часть mb-отрезка, которая приходится на единицу длины стороны треугольника.
, то есть представляет собой силу, приходящуюся на единицу площади. Подобно этому, индекс разносторонности представляет собой ту часть mb-отрезка, которая приходится на единицу длины стороны треугольника.
Условимся в дальнейшем употреблять следующие обозначения.
1) Будем считать, что против углов треугольника 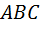 лежат стороны
лежат стороны  ,
,  ,
,  соответственно, для которых выполняется соотношение
соответственно, для которых выполняется соотношение
|
|
|

2) Длину mb-части стороны  будем обозначать через
будем обозначать через 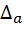 .
.
3) Индекс разносторонности угла 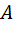 будем обозначать через
будем обозначать через 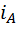 . В наших обозначениях
. В наших обозначениях

Дата добавления: 2019-09-13; просмотров: 206; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
