Типология алгебр и отсутствие «трёхмерных» чисел
3.4.3.1. Постановка задачи
Итак, мы построили три алгебры: комплексные, двойные и дуальные числа. Одна из этих алгебр – комплексные числа – оказалась алгеброй с делением. Действительно, любое комплексное число 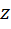 можно поделить на любое ненулевое число
можно поделить на любое ненулевое число 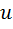 .
.
Опыт построения и изучения трёх алгебр наводит на мысль пойти дальше и рассмотреть «трёхмерные» числа вида 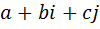 , где
, где 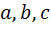 – произвольные действительные числа, а
– произвольные действительные числа, а  и
и 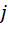 – некоторые символы. Можно было бы попытаться построить алгебру, которая удовлетворяет условиям теоремы 5, однако в книге [13, c. 16] сформулировано «запретительное» утверждение: алгебру трёхмерных чисел с делением построить невозможно! При этом не приведено никаких аргументов в пользу такого категоричного (и, что важно, непривычного) запрета.
– некоторые символы. Можно было бы попытаться построить алгебру, которая удовлетворяет условиям теоремы 5, однако в книге [13, c. 16] сформулировано «запретительное» утверждение: алгебру трёхмерных чисел с делением построить невозможно! При этом не приведено никаких аргументов в пользу такого категоричного (и, что важно, непривычного) запрета.
Здесь руководитель должен объяснить школьникам, что они попали в ситуацию, типичную для чтения научной литературы: некоторые факты формулируются без доказательства, так что для полного понимания текста читатель должен самостоятельно придумать их или отыскать их в других источниках.
Так перед школьниками возникает задача доказать утверждение, не доказанное в книге. Его точная формулировка будет приведена ниже, в разделе 3.4.3.4, а пока мы сконцентрируемся на необходимых сведениях и типологии алгебр.
3.4.3.2. Типология алгебр
В данном разделе собраны те понятия алгебры, которые потребуются для доказательства основного утверждения.
|
|
|
Прежде всего, мы формулируем понятие векторного пространства в том виде, в каком оно определено в вузовских учебниках, например, в книге [15].
Всюду, если не оговорено противное, мы будем использовать следующие соглашения. 1) Векторы обозначаются жирными латинскими буквами: 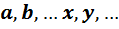 Нулевой вектор обозначается жирным символом
Нулевой вектор обозначается жирным символом 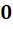 . 2) Все векторные пространства рассматриваются над полем вещественных чисел. Вещественные коэффициенты обозначаются, как правило, греческими буквами:
. 2) Все векторные пространства рассматриваются над полем вещественных чисел. Вещественные коэффициенты обозначаются, как правило, греческими буквами: 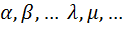
До сих пор мы употребляли термин «алгебра» в смысле естественного языка, то есть в его почти житейском смысле. Дадим теперь его точное определение.
Определение 1. Алгеброй 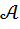 называется векторное пространство, в котором определено умножение векторов друг на друга, обладающее следующими свойствами.
называется векторное пространство, в котором определено умножение векторов друг на друга, обладающее следующими свойствами.
1) Выполняется левая и правая дистрибутивность, то есть
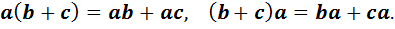
2) Выполняется однородность относительно умножения на вещественное число, то есть равенство
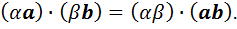
С помощью специальных определений выделим некоторые типы алгебр.
Определение 2. Алгебра называется коммутативной, если умножение обладает свойством
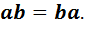
Определение 3. Алгебра называется ассоциативной, если умножение обладает свойством
|
|
|
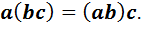
Определение 4. Алгеброй с единицей называется алгебра, в которой существует особый элемент 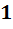 , такой, что для любого
, такой, что для любого 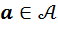 выполняются равенства
выполняются равенства
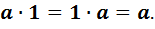
В дальнейшем символы 1 и 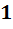 будут иметь разный смысл: первый означает вещественное число 1, а второй – единичный элемент алгебры.
будут иметь разный смысл: первый означает вещественное число 1, а второй – единичный элемент алгебры.
Определение 5. Алгебра называется алгеброй с делением, если для любого 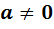 и для любого
и для любого  каждое из уравнений
каждое из уравнений 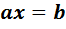 и
и 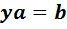 имеет единственное решение.
имеет единственное решение.
Определение 6. Подмножество 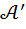 алгебры
алгебры 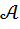 называется подалгеброй алгебры
называется подалгеброй алгебры 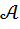 , если оно само является алгеброй относительно тех же самых операций сложения, умножения, умножения на вещественное число.
, если оно само является алгеброй относительно тех же самых операций сложения, умножения, умножения на вещественное число.
Определение 7. Две алгебры 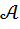 и
и 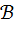 называются изоморфными, если существует отображение
называются изоморфными, если существует отображение 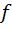 из алгебры
из алгебры 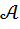 в алгебру
в алгебру 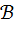 , которое обладает следующими свойствами:
, которое обладает следующими свойствами:
1) взаимной однозначностью;
2) 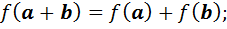
3) 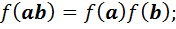
4) 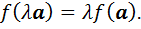
Разумеется, все понятия были проиллюстрированы примерами и, что не менее важно, контрпримерами из школьного курса математики.
3.4.3.3. Необходимые леммы
В данном подразделе собраны вместе те леммы, которые будут необходимы для доказательства основного утверждения раздела. Они были получены школьниками либо самостоятельно, либо с минимальной помощью научного руководителя.
|
|
|
Лемма 1. Многочлен третьей степени имеет корень. Он разлагается либо в произведение трёх линейных множителей, либо в произведение линейного множителя и квадратичного множителя с отрицательным дискриминантом.
Доказательство было получено участниками проекта традиционным для математического анализа методом в процессе ответов на вопросы руководителя.
Лемма 2. Если произведение двух элементов алгебры с делением равно нулю, то один из сомножителей равен нулю.
Доказательство. Исследуем сначала, чему равно произведение произвольного элемента 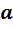 на нулевой элемент. Для этого вычислим выражение
на нулевой элемент. Для этого вычислим выражение 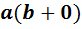 двумя способами. С одной стороны,
двумя способами. С одной стороны, 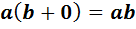 . С другой стороны,
. С другой стороны, 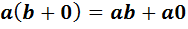 . Приравняем два результата:
. Приравняем два результата: 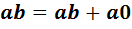 . Сократив на
. Сократив на 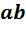 , получим, что
, получим, что 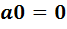 .
.
Пусть теперь 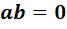 . Если
. Если 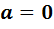 , то лемма доказана. Если
, то лемма доказана. Если 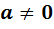 , то сопоставим уравнение
, то сопоставим уравнение 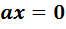 , равенство
, равенство 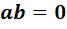 и результат первого этапа доказательства
и результат первого этапа доказательства 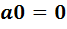 . Два последних равенства означают, что уравнение имеет решения
. Два последних равенства означают, что уравнение имеет решения 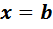 и
и 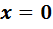 . В силу определения алгебры с делением решение является единственным, поэтому
. В силу определения алгебры с делением решение является единственным, поэтому 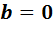 .
.
Лемма З. Ассоциативная алгебра с делением имеет единичный элемент.
|
|
|
Доказательство. 1) Очевидно, что сначала мы должны сконструировать единичный элемент. Для этого рассмотрим конкретный ненулевой элемент 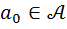 и уравнение
и уравнение 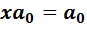 . Оно имеет решение
. Оно имеет решение 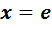 , в силу чего выполняется равенство
, в силу чего выполняется равенство
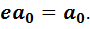 (4)
(4)
Теперь нам нужно доказать, что сконструированный элемент действительно является единичным, то есть обладает двумя следующими свойствами:
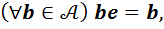 (5)
(5)
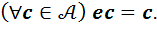 (6)
(6)
2) Для доказательства утверждения (5) рассмотрим произвольный элемент 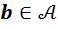 и проанализируем другое уравнение, а именно уравнение
и проанализируем другое уравнение, а именно уравнение
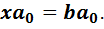 (7)
(7)
Очевидно, что оно имеет решение 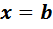 . С другой стороны, если мы домножим равенство (4) на
. С другой стороны, если мы домножим равенство (4) на  слева и воспользуемся ассоциативностью, то получим равенство
слева и воспользуемся ассоциативностью, то получим равенство
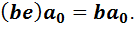 (8)
(8)
Сопоставив равенство (8) и уравнение (7), получим ещё одно решение 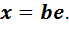 В силу единственности решения
В силу единственности решения 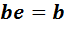 . Итак, утверждение (5) доказано.
. Итак, утверждение (5) доказано.
3) Для доказательства утверждения (6) рассмотрим произвольный элемент 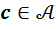 и проанализируем третье уравнение, а именно уравнение
и проанализируем третье уравнение, а именно уравнение
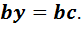 (9)
(9)
Очевидно, что оно имеет решение 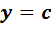 . С другой стороны, если мы домножим равенство (5) на
. С другой стороны, если мы домножим равенство (5) на 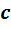 справа и воспользуемся ассоциативностью, то получим равенство
справа и воспользуемся ассоциативностью, то получим равенство
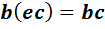 . (10)
. (10)
Сопоставив равенство (10) и уравнение (9), получим ещё одно решение 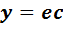 . В силу единственности решения
. В силу единственности решения 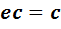 . Итак, утверждение (6), а вместе с ним и лемма в целом, доказаны.
. Итак, утверждение (6), а вместе с ним и лемма в целом, доказаны.
Мы привели полные доказательства лемм 2 и 3 для того, чтобы проиллюстрировать некое противоречие. С одной стороны, доказательства являются не слишком сложными. Действительно, в них не более трёх логических ходов, которые включают в себя простые действия: домножения равенств, использование ассоциативности, понятие решения уравнения. С другой стороны, они достаточно трудны для школьника, потому что требуют от него изощрённой логики, к которой он не привык: учёта некоммутативности умножения, скрупулёзного использования ассоциативности, работы с уравнениями неочевидного происхождения и т.п. По мнению автора, именно сочетание небольшой сложности и большой трудности обогащает интеллект участников проекта.
Следующая лемма носит геометрический характер. В то же время, она удивительным образом связана с аналитической леммой 1.
Лемма 4. Любой элемент 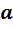 трехмерной алгебры
трехмерной алгебры 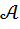 с единицей
с единицей 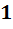 удовлетворяет равенству
удовлетворяет равенству 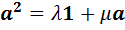 при подходящих коэффициентах
при подходящих коэффициентах 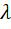 и
и 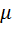 .
.
Доказательство. 1) Если 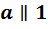 , то равенство очевидно, поэтому в дальнейшем рассматриваем случай
, то равенство очевидно, поэтому в дальнейшем рассматриваем случай 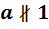 , то есть два линейно независимых вектора
, то есть два линейно независимых вектора 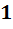 и
и 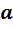 .
.
2) Рассмотрим теперь три вектора: 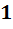 ,
, 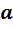 и
и 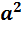 . Если они линейно зависимы, то именно добавленный вектор
. Если они линейно зависимы, то именно добавленный вектор 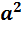 линейно выражается через два другие, а это и означает выполнение искомого равенства. В силу этого будем считать их линейно независимыми.
линейно выражается через два другие, а это и означает выполнение искомого равенства. В силу этого будем считать их линейно независимыми.
3) Итак, мы имеем базис из трёх векторов 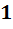 ,
, 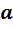 и
и 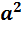 . Любой вектор, в частности
. Любой вектор, в частности 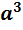 , линейно выражается через базисные векторы:
, линейно выражается через базисные векторы: 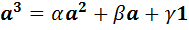 . Другими словами,
. Другими словами,
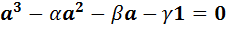 . (11)
. (11)
Рассмотрим многочлен 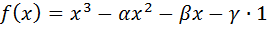 с теми же самыми коэффициентами, что и в равенстве (11). В силу леммы 1 он разлагается либо в произведение
с теми же самыми коэффициентами, что и в равенстве (11). В силу леммы 1 он разлагается либо в произведение 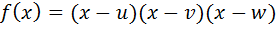 , либо в произведение
, либо в произведение 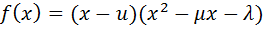 , где дискриминант квадратного трёхчлена отрицателен. Выясним, которая из этих двух возможностей действительно реализуется.
, где дискриминант квадратного трёхчлена отрицателен. Выясним, которая из этих двух возможностей действительно реализуется.
4) Допустим, что 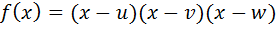 . Подставим вместо переменного
. Подставим вместо переменного 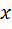 элемент
элемент 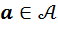 . В силу равенства (11) получим, что
. В силу равенства (11) получим, что 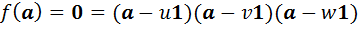 . Поскольку
. Поскольку 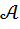 является алгеброй с делением, последнее равенство равносильно совокупности равенств
является алгеброй с делением, последнее равенство равносильно совокупности равенств 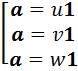 . Каждое из них означает, что вектор
. Каждое из них означает, что вектор 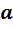 коллинеарен вектору
коллинеарен вектору 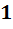 , а это противоречит соглашению пункта 1).
, а это противоречит соглашению пункта 1).
5) Допустим, что 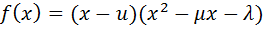 . Подставим вместо переменного
. Подставим вместо переменного 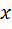 элемент
элемент 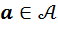 . В силу равенства (11) получим, что
. В силу равенства (11) получим, что 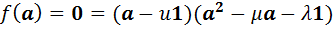 . Поскольку
. Поскольку 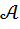 является алгеброй с делением, мы получаем совокупность равенств
является алгеброй с делением, мы получаем совокупность равенств 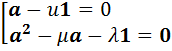 . Первое равенство выполняться не может, поскольку оно противоречит соглашению пункта 1). Следовательно, выполняется второе равенство, откуда следует, что
. Первое равенство выполняться не может, поскольку оно противоречит соглашению пункта 1). Следовательно, выполняется второе равенство, откуда следует, что 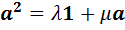 , а это и требовалось доказать.
, а это и требовалось доказать.
Следствие. Если 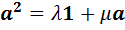 , то дискриминант квадратного трехчлена
, то дискриминант квадратного трехчлена 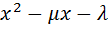 отрицателен.
отрицателен.
Лемма 5. Если элемент 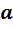 ассоциативной алгебры
ассоциативной алгебры 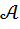 с делением не коллинеарен
с делением не коллинеарен 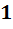 , то совокупность
, то совокупность 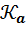 элементов вида
элементов вида 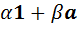 образует подалгебру, изоморфную алгебре комплексных чисел.
образует подалгебру, изоморфную алгебре комплексных чисел.
Доказательство. 1) Покажем сначала, что подмножество 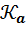 является подалгеброй. Для этого нужно показать его замкнутость относительно сложения, умножения и умножения на число.
является подалгеброй. Для этого нужно показать его замкнутость относительно сложения, умножения и умножения на число.
А) Пусть 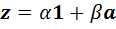 и
и 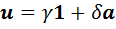 . Тогда
. Тогда 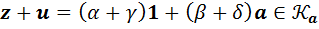 .
.
Б) Перемножая элементы 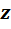 и
и 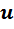 , получим, что
, получим, что 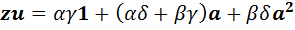 . Согласно лемме 4
. Согласно лемме 4 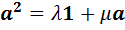 . Подставив его выражение в последнее равенство, раскрыв скобки и приведя подобные члены, получим, что
. Подставив его выражение в последнее равенство, раскрыв скобки и приведя подобные члены, получим, что 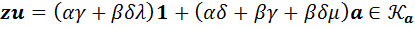
В) Замкнутость относительно умножения на число очевидна, поскольку 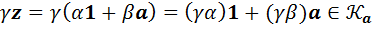 .
.
Итак, подмножество 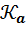 является подалгеброй алгебры
является подалгеброй алгебры 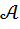 .
.
2) Покажем, что подалгебра 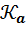 изоморфна алгебре комплексных чисел. Для начала перепишем равенство
изоморфна алгебре комплексных чисел. Для начала перепишем равенство 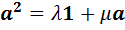 в виде
в виде 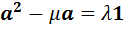 и выделим полный квадрат из левой части. Получим, что
и выделим полный квадрат из левой части. Получим, что
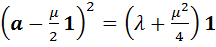 . (12)
. (12)
Дальнейшие рассуждения зависят от знака числового коэффициента в правой части.
А) Пусть 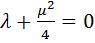 . Тогда равенство (12) примет вид
. Тогда равенство (12) примет вид 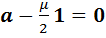 , а это означает, что вектор
, а это означает, что вектор 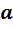 коллинеарен
коллинеарен 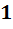 . Противоречие.
. Противоречие.
Б) Пусть 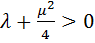 . Если считать, что
. Если считать, что 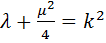 , то равенство (12) можно преобразовать к виду
, то равенство (12) можно преобразовать к виду 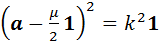 , откуда следует, что
, откуда следует, что 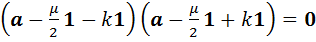 . Если
. Если 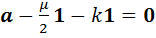 , то это означает, что вектор
, то это означает, что вектор 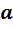 коллинеарен вектору
коллинеарен вектору 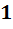 , а это противоречие. Аналогичное противоречие получим, если приравняем к нулю второй сомножитель последнего равенства.
, а это противоречие. Аналогичное противоречие получим, если приравняем к нулю второй сомножитель последнего равенства.
В) Пусть 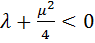 . Если считать, что
. Если считать, что 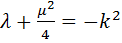 , то равенство (12) можно преобразовать к виду
, то равенство (12) можно преобразовать к виду 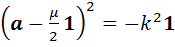 , откуда следует, что
, откуда следует, что
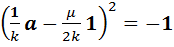 . (13)
. (13)
Введём обозначение 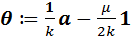 . В сочетании с равенством (13) оно означает следующее: во-первых,
. В сочетании с равенством (13) оно означает следующее: во-первых, 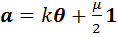 , и во-вторых,
, и во-вторых, 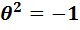 .
.
Подставим полученное выражение для 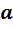 в выражение произвольного элемента подалгебры:
в выражение произвольного элемента подалгебры: 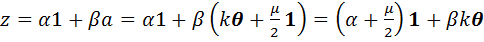 . Коэффициенты при
. Коэффициенты при 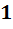 и
и 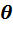 являются вещественными числами и
являются вещественными числами и 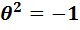 , поэтому подалгебра
, поэтому подалгебра 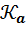 изоморфна алгебре комплексных чисел.
изоморфна алгебре комплексных чисел.
Здесь необходимо сделать два замечания. Первое из них касается употребления термина «лемма». С одной стороны, утверждения лемм 4 и 5 достаточно серьёзны, а доказательства их достаточно сложны. В силу этого они вполне могли бы называться теоремами. С другой стороны, нашей целью является доказательство утверждения об отсутствии «трёхмерных» чисел, поэтому все вспомогательные утверждения естественно называть леммами.
Второе замечание является гораздо более серьёзным и касается вопроса о том, могут ли школьники самостоятельно изобрести пять нетривиальных утверждений, высказанным в леммах 1–5. Очевидно, что ответ является отрицательным, поэтому пока не ясно, на каком основании эти леммы были включены в доклад школьников в качестве самостоятельного результата. Мы ответим на этот вопрос в разделе 3.4.4.
3.4.3.4. Доказательство основного утверждения
Сформулируем теперь наше основное утверждение
Теорема 6. Не существует трёхмерных ассоциативных алгебр с делением.
Доказательство. Допустим, что такая алгебра 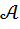 существует. Рассмотрим две различных подалгебры
существует. Рассмотрим две различных подалгебры 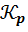 и
и 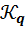 . Поскольку каждая из них изоморфна алгебре комплексных чисел, можно изначально выбрать векторы
. Поскольку каждая из них изоморфна алгебре комплексных чисел, можно изначально выбрать векторы 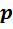 и
и 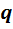 таки образом, чтобы
таки образом, чтобы 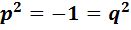 . Кроме того, в силу различия алгебр (то есть различия двух двумерных плоскостей в трёхмерном пространстве) векторы
. Кроме того, в силу различия алгебр (то есть различия двух двумерных плоскостей в трёхмерном пространстве) векторы 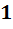 ,
, 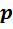 и
и 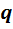 образуют базис.
образуют базис.
Разложим по базису произведение порождающих векторов:
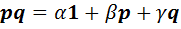 . (14)
. (14)
Пусть 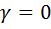 . Тогда равенство (14) примет вид
. Тогда равенство (14) примет вид 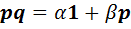 . Домножим новое равенство на элемент
. Домножим новое равенство на элемент 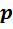 слева:
слева: 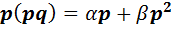 . Если воспользоваться ассоциативностью умножения и равенством
. Если воспользоваться ассоциативностью умножения и равенством 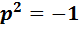 , то мы получим, что
, то мы получим, что 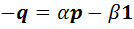 , откуда
, откуда 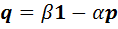 . Последнее равенство означает, что векторы
. Последнее равенство означает, что векторы 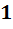 ,
, 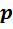 и
и 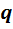 не образуют базис, что противоречит их построению.
не образуют базис, что противоречит их построению.
Пусть в равенстве (14) 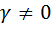 . Домножим его слева на элемент
. Домножим его слева на элемент 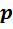 , а затем воспользуемся ассоциативностью и равенством
, а затем воспользуемся ассоциативностью и равенством 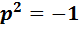 . Получим, что
. Получим, что 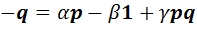 , откуда
, откуда
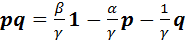 . (15)
. (15)
Каждое из равенств (14) и (15) представляет собой разложение вектора 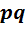 по базису. В силу единственности разложения мы можем приравнять соответствующие коэффициенты, в частности, третьи коэффициенты:
по базису. В силу единственности разложения мы можем приравнять соответствующие коэффициенты, в частности, третьи коэффициенты: 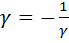 . Отсюда следует, что
. Отсюда следует, что 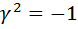 , а это невозможно для вещественного числа
, а это невозможно для вещественного числа 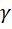 . Полученное противоречие означает ложность сделанного допущения и истинность теоремы.
. Полученное противоречие означает ложность сделанного допущения и истинность теоремы.
Педагогическая рефлексия
Обсудим теперь, насколько самостоятельными были школьники в процессе работы с леммами 1–5 и теоремой 6.
Анализ вопроса целесообразно начать с того, что чтение учебников, к которому привыкли школьники, серьёзно отличается от чтения дополнительной литературы. Дело в том, что эти два вида книг используются для достижения разных целей. Работа с учебником проводится с целью передачи системы знаний и умений, поэтому учебники, как правило, читаются последовательно, страница за страницей, и переход к последующей теме возможен только после усвоения предыдущей. Дополнительная литература читается с иными целями: с целью поиска информации, необходимой для решения возникшей ранее задачи; с целью постановки новой исследовательской задачи; с общей целью выбора области для будущей исследовательской деятельности… В силу сказанного чтение дополнительной литературы обладает несколькими важными особенностями: нелинейностью чтения, избирательностью чтения и скрупулёзностью анализа текста [37].
В нашем случае названные особенности проявились следующим образом. В аннотации ко книге [13, с. 2] сказано, что целью её является «разыскание «алгебр с делением» (теорема Фробениуса)…». Заглянув на стр. 117, мы находим её формулировку.
Теорема (Г. Фробениус, 1878 г.). Любая ассоциативная алгебра с делением изоморфна одной из трёх алгебр: алгебре действительных чисел, алгебре комплексных чисел или алгебре кватернионов.
При всей серьёзности и «молодости» этой теоремы (изобретённой менее 150 лет назад) в ней почти все если не понятно, то знакомо. Действительно, термины «алгебра» и «ассоциативность» вполне привычны, заклинанию «на ноль делить нельзя» не сложно придать расширительный смысл, так что непонятными остаются всего лишь два термина: «изоморфизм» и «кватернион».
Вернувшись к началу, то есть к последовательному чтению книги, мы на стр. 16 находим утверждение теоремы 6. Оно интересно и неинтересно одновременно. С одной стороны, если человек знает теорему Фробениуса, то из неё мгновенно вытекает теорема 6, так что все тривиально. С другой стороны, а знаем ли мы теорему Фробениуса? Скорее нет, т.к. два термина пока не понятны, не говоря уже о доказательстве. Так перед школьниками возникает альтернатива: освоить теорему Фробениуса и вывести из неё теорему 6 или сконструировать её независимое доказательство.
Изучение теоремы Фробениуса мгновенно уничтожит проект, т.к. вместо исследовательской деятельности школьникам придётся заняться деятельностью учебной, то есть слушать лекции, читать книги, выполнять тренировочные упражнения. К тому же неизбежно возникнут вопросы, деструктивные в данной ситуации: зачем все это нужно, почему мы изучаем именно эту область, а не иную, и проч. Наконец, руководителю известно, что доказательство теоремы Фробениуса является весьма сложным. Во всяком случае, оно никогда не изучалось в педагогических вузах, так что нужны веские причины для его изучения детьми. Так мы приходим к необходимости отыскать самостоятельное доказательство теоремы 6.
Первый шаг поиска прост, поскольку «запретительные» утверждения часто доказывается методом от противного. Но уже следующий шаг полностью непонятен. Единственный ориентир состоит в том, чтобы посмотреть, каким способом доказывается теорема Фробениуса, и модифицировать этот способ для трёхмерного пространства. Таким образом, мы вынуждены вновь обратиться к «далёким» страницам книги [13, c. 117–120]. Там мы обнаруживаем, что существенную роль в доказательстве играют подалгебры 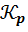 и
и 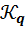 , конструируемые особым способом и обладающие специальными свойствами. Так перед школьником-исследователем постепенно возникает лемма 5, а затем леммы 4, 3, 2, 1. Так школьник постепенно понимает, что логика исследования и логика изложения отличаются друг от друга.
, конструируемые особым способом и обладающие специальными свойствами. Так перед школьником-исследователем постепенно возникает лемма 5, а затем леммы 4, 3, 2, 1. Так школьник постепенно понимает, что логика исследования и логика изложения отличаются друг от друга.
Попытаемся дать теореме 6 качественную характеристику путём её отнесения к тому или иному классу теорем. Можно было бы назвать её «запретительной теоремой», как мы уже писали ранее, однако такой термин не используется. Можно было бы назвать её «теоремой отсутствия» в том смысле, который противоположен смыслу словосочетания «терема существования». К сожалению, и этот термин не используется. Можно было бы считать её классификационной теоремой, однако этому препятствует характер полученного результата – классифицируемых объектов (алгебр со специальными свойствами) не существует. В конце концов, мы назвали её «слабой формой теоремы Фробениуса» на том основании, что доказательство теоремы 6 представляет собой модификацию доказательства теоремы Фробениуса применительно к размерности 3.
По мнению автора, все сказанное позволяет считать, что школьники были вполне самостоятельны (или достаточно самостоятельны) в своей математической деятельности.
В заключение отметим красоту доказательства теоремы 6. Распространённый способ получения противоречия состоит в том, чтобы получить для одного вектора два разных разложения по базису. Где же взять такой вектор? Тут мы и обнаруживаем, что в нашем распоряжении есть только два вектора 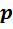 и
и 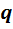 , порождающие подалгебры. В этих условиях рассмотрение произведения
, порождающие подалгебры. В этих условиях рассмотрение произведения 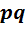 и вся последующая эквилибристика почти неизбежны.
и вся последующая эквилибристика почти неизбежны.
Дата добавления: 2019-09-13; просмотров: 368; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
