В поисках «самого неправильного» треугольника
До сих пор мы определяли индексы разносторонности отдельных углов треугольника, однако не определяли меру разносторонности треугольника в целом. Сформулируем её определение.
Определение 3. Индексом разносторонности треугольника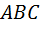 
, стороны которого удовлетворяют соотношениям 
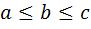, называется число
С геометрической точки зрения в определении 3 речь идёт об алгебраической сумме сторон треугольника из предложения 11: из суммы двух коротких сторон треугольника вычитается самая длинная его сторона.
Предложение 12. Индекс разносторонности треугольника принадлежит промежутку [0; 1).
Доказательство немедленно следует из того факта, что каждый из индексов разносторонности угла принадлежит промежутку [0; 0,5).
Заметим, что оценка сверху является весьма грубой и ниже будет существенно уточнена.
Теорема 13. Индекс разносторонности треугольника равен нулю тогда и только тогда, когда треугольник является равнобедренным.
Доказательство. В силу формулы (6) определение индекса разносторонности треугольника может быть переписано в виде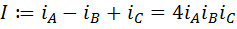 
. Если 
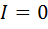, то один из сомножителей последнего произведения равен нулю, а это значит, что треугольник является равнобедренным. Обратно, если треугольник является равнобедренным, то один из сомножителей равен нулю, а значит и .
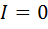Предложения 9 и 13 означают, что для равнобедренных треугольников достигается нижняя граница того числового промежутка, которому, согласно предложению 12, должен принадлежать индекс разносторонности треугольника. Поставим теперь задачу о точном определении верхней границы индекса разносторонности треугольника.
|
|
|
Задача 2. Какова точная верхняя грань индекса разносторонности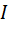 
треугольника? Достигается ли она?
Образно говоря, мы решаем задачу о том, «насколько разносторонним» может быть треугольник и существует ли «самый разносторонний» треугольник.
Прежде всего, введём необходимые обозначения, переводящие задачу 2 на язык формул.
Пусть средняя сторона 
. Тогда две другие стороны треугольника удовлетворяют неравенствам 
и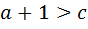 
. Это означает, что для решения задачи 2 нужно будет установить наличие или отсутствие глобального экстремума функции 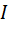в незамкнутой ограниченной области 
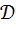(рис. 35), задаваемой системой неравенств
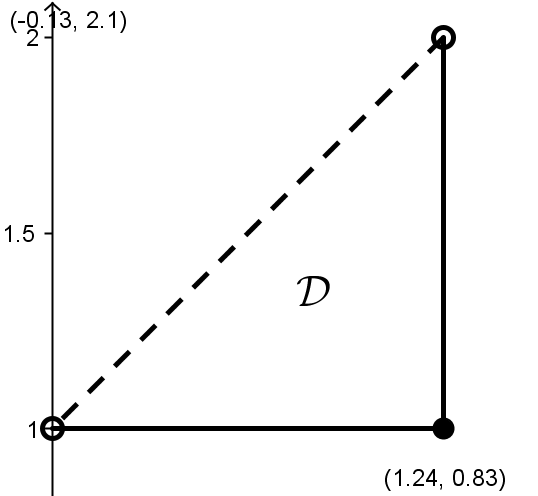
Рис. 35. Область для поиска глобального экстремума
Начнём с того, что решим вспомогательную задачу.
Задача 
Найдите глобальный экстремум функции 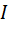в замкнутой ограниченной области 
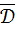, задаваемой системой неравенств
Решение задачи основано на трёх леммах.
Лемма 1. Функция 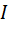не имеет локальных экстремумов внутри области .
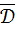Доказательство. Прежде всего, выразим функцию 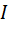через стороны треугольника. По формулам (9) и (5) получим, что
|
|
|
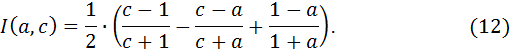
Функция 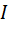представляет собой сумму рациональных функций от двух аргументов, которая не обращается в нуль внутри области 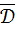. В силу этого в экстремальной точке, если таковая существует, должны обращаться в нуль частные производные 
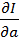и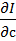 
.
Применяя формулы дифференцирования и приводя подобные члены, находим, что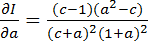 
и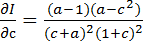 
. Приравняв к нулю частные производные, получим систему 
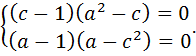Она распадается на совокупность четырех систем и дает два решения: 
и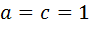 
. Первая точка лежит вне области 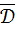, а вторая – на ее границе, что и доказывает лемму.
Лемма 2. На горизонтальной и вертикальной частях границы области 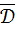функция 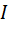тождественно равна нулю.
Доказательство. На горизонтальной части границы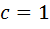 
, поэтому формула (12) принимает вид 
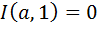. На вертикальной части границы 
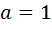, поэтому формула (12) принимает вид 
.
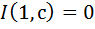Заметим, что лемму 2 можно вывести из геометрических соображений, поскольку горизонтальная и вертикальная части границы области 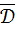соответствуют равнобедренным треугольникам.
Лемма 3. Наклонная часть границы области 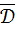содержит точно одну точку локального экстремума 
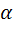. При этом точка 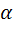является корнем уравнения 
, принадлежит интервалу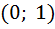 
и представляет собой точку локального максимума.
|
|
|
Доказательство. Для наклонной части границы области 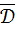выполняются соотношения 
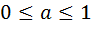и 
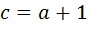, поэтому формула (12) принимает вид
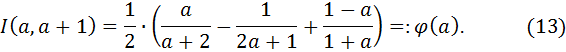
Дифференцируя функцию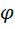 
, получим, что 
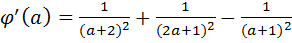. Приводя дроби к общему знаменателю, а затем приводя подобные члены, получим, что 
.
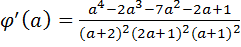Очевидно, что для поиска точек экстремума функции 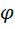нужно найти корни и промежутки знакопостоянства многочлена 
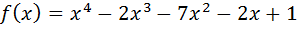. Это можно сделать разными способами.
Прежде всего, можно построить в интерактивной математической среде график многочлена 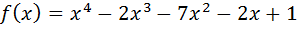и наглядно увидеть, что он имеет точно один корень на отрезке [0; 1]. Приближенное с недостатком значение этого корня с точностью до 10 знаков получено нами в среде GeoGebra. Оно таково: 
.
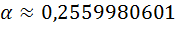Кроме того, можно вычислить значения многочлена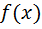 
в точках 
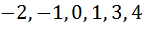и по чередованию знаков убедиться, что многочлен имеет точно один корень на каждом из отрезков 
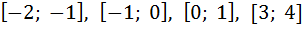. Приближенное значение корня на отрезке 
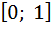можно найти любым из известных методов.
Наконец, можно решить уравнение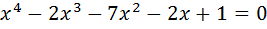 
методом Феррари и выразить в радикалах точное значение корня .
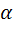Теперь решение задачи 2 может быть сформулировано в виде следующей теоремы.
Теорема 14. Точная верхняя грань множества значений индекса разносторонности 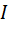треугольника по незамкнутой области 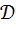равна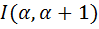 
. Она не достигается.
|
|
|
Доказательство. 1) Из лемм 1–3 следует, что точка с координатами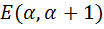 
является точкой глобального экстремума функции 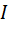в замкнутой области 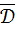, поэтому для любой точки 
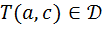выполняется неравенство 
.
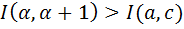2) Соединим точк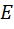и 
и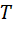 
отрезком. В силу непрерывности функции 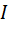в области 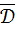она принимает все значения между 
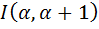и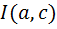 
.
3) Из двух предыдущих пунктов доказательства следует, что число 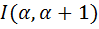является точной верхней гранью изучаемого множества. Поскольку неравенство в первом пункте доказательства является нестрогим, точная верхняя грань не достигается.
Следствие 1. Индекс разносторонности треугольника принадлежит промежутку [0; 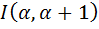) и принимает все значения из этого промежутка.
Сформулируем не вполне строгий, «вольный», качественный результат решения задачи 2. Он состоит в том, что «самого разностороннего» треугольника не существует в природе, и что для любого треугольника можно построить другой треугольник с бо́льшим индексом разносторонности.
Следствие 2. Точная верхняя грань множества значений индекса разносторонности приближённо равна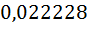 
.
Доказательство. По теореме 14 получаем, что
.
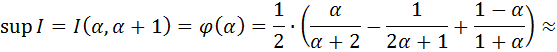
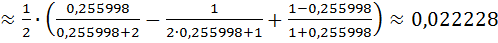В заключение приведём алгоритм построения динамического чертежа, с помощью которого можно строить треугольники, у которых значения индекса разносторонности приближаются к верхней грани.
1. С помощью инструмента Отрезок с фиксированной длиной постройте вспомогательный отрезок длины 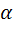, выбрав при этом достаточно точное значение числа .
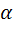2. С помощью инструмента Отрезок с фиксированной длиной постройте отрезок 
длины 1.
3. С помощью инструмента Циркуль постройте окружность радиуса 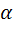с центром в точке 
.
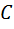4. С помощью инструмента Точка на объекте постройте точку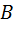 
на окружности.
5. С помощью инструмента Отрезок постройте отрезки 
и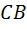 
.
Треугольник 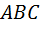является искомым. При стремлении точки 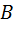вдоль окружности к точке пересечения окружности с продолжением стороны индекс разносторонности треугольника будет стремиться к своей точной верхней грани.
Педагогическая рефлексия
Нетрудно видеть, что с технической точки зрения материал подразделов 3.3.1–3.3.3 является весьма простым и вполне доступен для школьников 8 класса. Несколько сложнее раздел 3.3.4, однако автор убеждён, что при помощи научного руководителя одарённый старшеклассник вполне может освоить его содержание.
Здесь с неизбежностью встаёт вопрос о мере той помощи, которую вправе оказывать научный руководитель, потому что вопрос этот порождает неприятную и трудноразрешимую дилемму. С одной стороны, можно было бы предложить школьнику «не просчитанную» задачу, решение которой до конца неизвестно даже научному руководителю. В этом случае его работа вполне может называться научной, однако весьма велика вероятность того, что команде «руководитель–ученик» не удастся получить сколько-нибудь значимых результатов. Было бы неэтичным подвергать команду серьёзному риску неудачи. С другой стороны, если предложить школьнику хорошо просчитанную задачу, то возникает вопрос об авторстве полученного результата. Излагая на конференции школьников «собственный» научный результат, ученик может внутренне осознавать свою несамостоятельность, а такая коллизия может нанести серьёзный ущерб нравственному воспитанию молодого человека.
По-видимому, в настоящее время вопрос о мере допустимой помощи школьнику не имеет общепринятого решения, так что каждый руководитель отвечает на него в соответствии с собственным опытом и мировоззрением. Автор с удовольствием высказывает своё субъективное мнение о том, что в большинстве случаев вышеупомянутая дилемма разрешается достойно.
Дата добавления: 2019-09-13; просмотров: 279; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!