Гиперкомплексные числа малых размерностей. Часть 1
Предварительные замечания
Проект, описанный в данном разделе, отличается от двух предыдущих в целом ряде отношений. Если предыдущие проекты относились к геометрии, то в настоящем проекте решались чисто алгебраические задачи. Кроме того, каждый из предыдущих проектов был реализован в течение одного года одним исполнителем, в то время как настоящий проект был рассчитан на двух исполнителей, которые работали над ним в течение двух последних классов школы. Другими словами, проект занял три года (2002–2003 и 2003–2004 учебные года). Третье отличие состоит в «возрастной ориентации» проекта, если так можно выразиться. Геометрические проекты рождались буквально на страницах учебника и не требовали от школьника дополнительной информации. Они вполне могли быть реализованы юношей/девушкой из 8-го или 9-го класса. Алгебраический проект был ориентирован на учащихся старших классов. В нем использовалась серьёзная дополнительная литература [13], которая, впрочем, «рассчитана на учащихся математических школ и просто всех интересующихся математикой» [13, с. 5]. Содержание проекта сознательно было выбрано настолько сложным, чтобы его реализация потребовала от исполнителей всего их интеллектуального багажа и серьёзных волевых усилий.
Здесь автор должен признаться, что как руководитель проекта он допустил ошибку, которая, к счастью, не оказалась фатальной. Дело в том, что восприятие необходимой математической информации и решение основных задач оказалось несколько более трудным для исполнителей, чем это предполагалось в начале работы. Впрочем, эти трудности были преодолены благодаря большой концентрации школьников и методическим усилиям руководителя. В нашей ситуации в полной мере подтвердилась мысль основателя кибернетики Н. Винера: «Математика – наука молодых. Иначе и быть не может. Занятия математикой – это такая гимнастика ума, для которой нужны вся гибкость и вся выносливость молодости» [6, c. 37].
|
|
|
В нижеследующем описании проекта причудливым образом переплелась информация двух типов. С одной стороны, часть сведений о гиперкомплексных числах была усвоена школьниками стандартным учебным способом, то есть из лекций и практических занятий научного руководителя и из чтения книг. С другой стороны, самая важная часть информации была получена школьниками самостоятельно в процессе решения ими исследовательских задач. Для того чтобы ярче высветить личные результаты школьников, мы используем следующий приём: текст, содержащий описание работы руководителя и учебную информацию, будет отмечен вертикальной чертой на полях. Это соглашение будет действовать на протяжении разделов 3.4.2 и 3.4.3.
|
|
|
Двумерные алгебры и первая классификационная теорема
С самого начала работы было ясно, что для реализации проекта исполнителям потребуется освоить существенный дополнительный материал. Для его освоения в условиях ограниченных временны́х ресурсов была выбрана следующая структура работы.
Комплексные числа были изучены в сентябре, то есть задолго до того времени, которое было предусмотрено программой математической школы. Для единообразия изложения и введения необходимых обозначений приведём схему изложения теории комплексных чисел. Сразу скажем, что источники информации для школьников были сознательно выбраны контрастными в следующем смысле: лекционное изложение делало акцент на формальной стороне теории, а необходимые мотивировки и содержательные подходы извлекались ими из книги [13], чтение которой считалось обязательным. Разумеется, руководитель не жалел времени на сопоставление двух подходов, если это было необходимо.
Итак, комплексным числом называется выражение вида
, где 
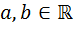и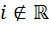 
.
Сложение комплексных чисел и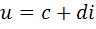 
определяется покомпонентно, то есть с помощью равенства
Всюду в дальнейшем будет подразумеваться, что сложение, в каких бы алгебрах оно ни происходило, определено покомпонентно.
|
|
|
Умножение комплексных чисел определяется с помощью равенства
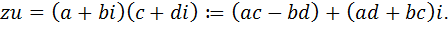(1)
Теорема 1. Свойства сложения и умножения комплексных чисел являются теми же самыми, что и свойства сложения и умножения действительных чисел:
1) сложение коммутативно, ассоциативно, имеет нейтральный элемент 
, любой элемент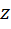 
обратим в том смысле, что существует элемент 
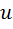, который в сумме с 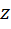дает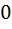 
;
2) умножение коммутативно, ассоциативно, имеет нейтральный элемент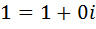 
, любой ненулевой элемент 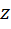обратим в том смысле, что существует элемент 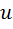, который в произведении с 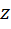дает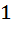 
;
3) умножение дистрибутивно относительно сложения.
В процессе изучения часть свойств была доказана на лекциях, а другая часть получена школьниками самостоятельно.
Следующая теорема непосредственно вытекает из формулы (1).
Теорема 2. Умножение комплексных чисел обладает следующими свойствами.
1) 
;
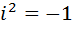2) Чтобы умножить комплексное число на вещественное, нужно каждый компонент комплексного числа умножить на вещественное число.
3) Если оба комплексных сомножителя 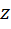и 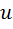являются вещественными числами, то их произведение, определяемое формулой (1), совпадает с умножением действительных чисел.
|
|
|
Доказательство. 1) Прямым вычислением по формуле (1) получаем, что
2) Вещественность комплексного числа 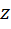означает, что 
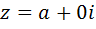. Подставляя 
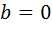в формулу (1), получим, что 
.
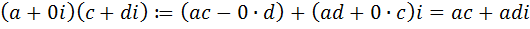3) Третье утверждение получается аналогично.
По завершении построения алгебры 
комплексных чисел школьникам были предъявлены две другие, «родственные» им алгебры: алгебра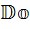 
двойных чисел и алгебра 
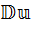дуальных чисел. (В обозначениях участвуют две первые буквы английских слов double – двойной и dual – дуальный.)
Двойным числом называется выражение вида
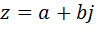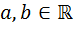, где и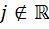 
.
Сложение двойных чисел 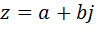и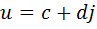 
определяется покомпонентно, а умножение – с помощью равенства
(2)
Дуальным числом называется выражение вида
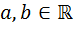, где и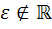 
.
Сложение дуальных чисел и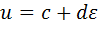 
определяется покомпонентно, а умножение – с помощью равенства
(3)
Первая задача носила, если так можно выразиться, общенаучный характер.
Задача 1. Попарно сравните три алгебры: комплексные числа , двойные числа 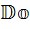и дуальные числа .
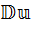Обсуждение. В определённом смысле программа действий школьников достаточно очевидна. Действительно, сравнить два объекта – это значит выявить их сходные и различные свойства. При этом длинный список свойств комплексных чисел был получен ранее. Это означает, что нужно было рассмотреть каждое из свойств комплексных чисел из теорем 1 и 2 и проверить, выполняется ли оно в алгебре двойных (дуальных) чисел. Таким образом, программа действий является хотя и обширной, но достаточно простой, особенно если учесть, что образец действий по проверке того или иного свойства был предъявлен при изучении комплексных чисел.
В результате школьники получили следующие утверждения.
Теорема 3. 1) Элемент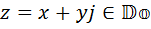 
необратим по умножению тогда и только тогда, когда 
.
2) Мнимая единица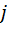 
обладает свойством 
.
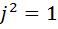3) Остальные свойства комплексных чисел, фигурирующие в теоремах 1 и 2, справедливы для алгебры двойных чисел.
Образно говоря, двойные числа отличаются от комплексных в двух отношениях: в них «много» элементов, необратимых по умножению, и мнимая единица имеет иное характеристическое свойство.
Теорема 4. 1) Элемент 
необратим по умножению тогда и только тогда, когда 
.
2) Мнимая единица 
обладает свойством 
.
3) Остальные свойства комплексных чисел, фигурирующие в теоремах 1 и 2, справедливы для алгебры дуальных чисел.
Вновь мы можем сказать, что дуальные числа отличаются от комплексных в двух отношениях: в них «много» элементов, необратимых по умножению, и мнимая единица имеет иное, уже третье по счету, характеристическое свойство.
Здесь наступает один из психологически важных моментов проекта, потому что школьники сталкиваются с необычной, новой для себя ситуацией. Дело в том, что на координатной плоскости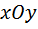 
каждый радиус-вектор 
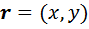с координатам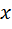и 
и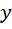 
может быть истолкован тремя разными способами: как комплексное число 
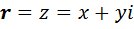, как двойное число 
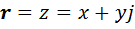и как дуальное число 
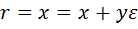. Другими словами, мы построили три различные двумерные алгебры. В этих условиях любой любопытный человек, даже далёкий от математики, может поставить естественный вопрос: а есть ли ещё какие-то двумерные алгебры, отличные от перечисленных? Итак, перед участниками проекта возникает следующая задача.
Задача 2. Перечислите все двумерные алгебры, которые можно было бы считать «числами» на том основании, что они обладают большинством свойств, описанных в теоремах 1 и 2.
Ответом на этот вопрос служит следующая теорема.
Теорема 5. Пусть двумерная алгебра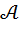 
, состоящая из элементов вида 
( 
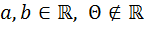), обладает следующими свойствами.
1) Умножение действительного числа 
на произвольный элемент алгебры 
дает тот же результат, что и в случае комплексных чисел, то есть
2) Выполняется однородность относительно умножения на вещественное число, то есть равенство
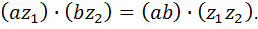
3) Имеет место левая и правая дистрибутивность, то есть
Тогда алгебра есть фактически одна из трех следующих алгебр: комплексных чисел, двойных чисел, дуальных чисел.
Таким образом, знакомство школьников с классификациями математических объектов переходит на новый уровень. Если раньше они осваивали системы определений, классифицирующих объекты (простые и составные числа; остроугольные, прямоугольные и тупоугольные треугольники), то теперь они встретились с теоремой, классифицирующей объекты.
Теорема 5 доказана в книге [13, § 2]. Школьники осваивали её как с помощью лекций руководителя, так и посредством чтения. Важно, что доказательство содержит некую конструкцию, которая была использована в процессе дальнейших самостоятельных исследований.
Дата добавления: 2019-09-13; просмотров: 262; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!