Дуалистические свойства математики
В школьном курсе: обзор
Как уже говорилось во Введении, первоначальное знакомство школьников с элементами методологии математики может происходить в процессе выявления таких свойств математики, которые не зависят ни от области математических исследований, ни от уровня исследований, ни от исторического периода развития математики. Перечни таких свойств могут быть различными. Мы будем ориентироваться на простую систему из четырёх дуалистических свойств математики, о которых говорилось во Введении. В книге [40, гл. 1] подробно обосновано объективное существование каждого из дуалистических свойств и показана возможность их использования для конструирования конкретных педагогических сценариев.
Приведём некоторые конкретные рекомендации по конструированию педагогических сценариев.
1) Целесообразно предлагать школьникам такие задания, в процессе выполнения которых они смогут сделать некоторые самостоятельные выводы.
Благодаря таким заданиям школьники будут знакомиться не только с новыми математическими фактами, но и участвовать в процессе их получения. Тем самым на уроках будет проиллюстрировано наличие деятельностно-продуктивного дуализма математики.
2) Целесообразно распределять задания между частями класса с целью получения каждой микрогруппой таких утверждений, которые будут служить предметом информационного обмена.
В процессе информационного обмена на уроках будет проиллюстрировано наличие личностно-социального дуализма математики.
|
|
|
3) Целесообразно формулировать задания таким образом, чтобы при их выполнении приходилось делать как индуктивные, так и дедуктивные умозаключения.
Благодаря таким заданиям на уроках будет проиллюстрировано наличие индуктивно-дедуктивного дуализма математики.
4) В практике преподавания уже давно существует традиция, которая состоит в выявлении естественнонаучного происхождения некоторых важных математических понятий: производной, интеграла и т.д. Целесообразно усилить эту традицию путём рассмотрения задач, приводящих к понятиям школьного курса математики: функции, уравнения, вероятности и т.д.
Благодаря таким заданиям на уроках будет проиллюстрировано наличие эмпирико-теоретического дуализма математики.
Важно, что сделанные рекомендации не просто обобщают опыт конкретного преподавателя математики, или являются точкой зрения научной школы, или обоснованы психологами, или широко распространены и т.п. Важно, что они описывают неотъемлемые свойства математики и, следовательно, существуют объективные причины, которые побуждают преподавателей следовать этим рекомендациям.
|
|
|
Сколь бы естественными и разумными ни казались высказанные советы, они нуждаются в конструктивном доказательстве их полезности в виде конкретных сценариев, которые можно было бы оценить путём анализа их происхождения, метода их конструирования, способов их применения и, наконец, достигнутых педагогических результатов. Таких сценариев достаточно много, хотя, разумеется, они не покрывают всего содержания обучения. К тому же они рассеяны по литературе и относятся не только к школьному, но и к вузовскому курсу математики.
Приведём краткий обзор, в котором обозначим те источники, по которым можно познакомиться со сценариями описанного типа. Мы надеемся, что знакомство с ними вдохновит читателя на создание собственных материалов той же идейной направленности. В своём обзоре мы коснёмся только того математического материала, который относится к школьному курсу.
Геометрия. Хорошо известно, что теорема Пифагора имеет многочисленные доказательства. Естественно, что существуют не менее многочисленные сценарии изучения этой замечательной теоремы. В книге [40, разд. 1.4.4] школьникам, не знакомым с теоремой Пифагора, предлагается научная задача об изучении свойств прямоугольных треугольников. Сценарий построен таким образом, что в процессе его реализации выявляются все четыре дуалистических свойства математики. Главное состоит в том, что формулировка теоремы Пифагора появляется в процессе словесного описания результатов самостоятельной (или почти самостоятельной) деятельности школьников.
|
|
|
Другой сценарий относится к стереометрии [42]. В нем предложена подборка провокационных (внутренне противоречивых) задач, подобных следующей: найдите объем правильной четырёхугольной пирамиды, у которой сторона основания равна 4, а угол между боковыми гранями равен 90°. В процессе решения, но не ранее, выясняется, что таких пирамид не существует! С подобным обстоятельством сталкивается несколько микрогрупп школьников, поскольку однотипные провокационные задачи разного содержания были предложены нескольким микрогруппам. Так возникает повод для обмена информацией и, в более общем плане, вопрос о допустимых соотношениях между элементами геометрических фигур. Изучение допустимых соотношений – это хороший повод для занятий, существенно углубляющий знания школьников.
Анализ. В книге [40, разд. 1.5.3] рассмотрен сценарий изучения взаимосвязей между чётностью, периодичностью и дифференцируемостью функций. При его реализации школьники получают теоремы следующего типа: если функция является чётной и дифференцируемой, то её производная является нечётной. Даже если кто-то сочтёт теорему малополезной, для нас важно, что она получена школьниками самостоятельно.
|
|
|
В статье [34] рассматривается сравнение скоростей изменения функции и её аргумента. Более точно, даётся ответ на четыре модификации одного вопроса: на каком промежутке из области определения
· функция растёт быстрее, чем растёт её аргумент;
· функция растёт медленнее, чем растёт её аргумент;
· функция убывает быстрее, чем растёт её аргумент;
· функция убывает медленнее, чем растёт её аргумент?
Эти вопросы формулируются применительно ко всем функциям из школьного курса: степенным функциям при разных показателях степеней, показательным функциям при разных основаниях, логарифмическим функциям при разных основаниях, тригонометрическим и обратным тригонометрическим функциям. Тем самым поиск ответа на вопросы становится чересчур трудоёмким для одного человека и требует организации групповой работы. Отсюда с неизбежностью выявляется личностно-социальный, индуктивно-дедуктивный и деятельностно-продуктивный дуализм математики.
Алгебра. В статье [34] описано простое наблюдение над квадратными уравнениями, которое может послужить основой продуктивного сценария и дать школьникам пищу для размышлений. Пусть, например, домашнее задание состояло в решении четырёх квадратных уравнений, которые выписаны вместе с их решениями в виде таблицы:
| Уравнения | Корни | Уравнения | Корни |
|  , 
| 
|  , 
|
|  , 
| 
|  , 
|
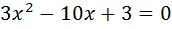
Как правило, школьники обращают внимание на ряд особенностей: а) на особенности корней данных уравнений; б) на связь корней с коэффициентами уравнений; в) на взаимосвязь между коэффициентами уравнения. В этих условиях учитель ставит естественную задачу по обобщению сделанных наблюдений и выражению этого обобщения в словесной форме. Когда (и если) это удаётся сделать, то школьникам предлагаются два задания: а) по общему правилу составить новые уравнения данного вида и проверить правильность сделанного предположения, решив их; б) провести строгое доказательство сформулированного утверждения. Заметим, что в данном случае доказательство сформулированного утверждения имеет ряд особенностей, хотя и выполняется по хорошо известным формулам для решения квадратных уравнений.
Другой алгебраический сценарий также приведён в статье [34]. Он базируется на большой коллекции из 14-ти однородных уравнений разных типов: однородных алгебраических уравнениях с двумя переменными; однородных тригонометрических уравнениях с одним переменным; однородных уравнениях с двумя переменными разных типов, а именно, неизвестного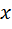 
и тригонометрической функции 
; однородных уравнениях с параметрами последнего из упомянутых типов. Следует заметить, что разнотипность переменных придаёт алгебраическому сценарию аналитический компонент. Действительно, однородное уравнение 
при положительных 
сводится к совокупности уравнений 
. Очевидно, что данная совокупность не может быть решения аналитическими методами, поэтому определение количества её решений на некотором интервале связна с построением графиков функций.
В заключение раздела дадим ещё несколько разнохарактерных ссылок. По мнению автора, иллюстрация эмпирико-теоретического дуализма математики вызывает наибольшие трудности. Именно поэтому гл. 6 книги [40] посвящена именно ему. Связь продуктивных сценариев обсуждаемого в книге типа и междисциплинарного подхода к преподаванию отражена в статье [35], а их связь с компетентностным подходом – в статье [34].
Глава 3
БОЛЬШИЕ ПРОЕКТЫ
Решение задач является наиболее характерной и специфической разновидностью свободного мышления.
Уильям Джеймс
В главе предложено описание нескольких больших проектов, выполненных школьниками под руководством автора. Цель каждого из них была, фактически, заявлена во Введении: предоставить исполнителям возможность приобретения опыта полномасштабного личного исследования в области математики. В этом описании предпринята попытка не только представить конечный математический результат, но и описать процесс его получения, отделив педагогическую работу руководителя от математической работы исполнителя.
Дата добавления: 2019-09-13; просмотров: 182; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!