Теорема о медианах треугольника
1. Отступим от основной линии нашего изложения и отметим, что повторные, уточняющие эксперименты в области физики составляют её неотъемлемую часть. Например, оценки и прямые измерения скорости света в вакууме происходят в течение вот уже 400 лет, начиная с 1620 г. (О. Рёмер) и далее в 1728 г. (Дж. Брэдли), в 1849 г. (Ф. Физо), в 1876 г. (М. Корню), в 1902 г. (А. Перротен), в 1926 г. (А. Майкельсон), в 1950 г. (Э. Бергштранд). Наконец, в 1975 г. Генеральная конференция по мерам и весам установила «окончательное» значение скорости света. Интересно, что для этого пришлось переписать в других терминах эталонное определение метра.
Покажем, что физический подход может быть полезен при изучении такой классической математической теоремы, какой является теорема о медианах треугольника. С этой целью рассмотрим несложный педагогический сценарий.
2. В предыдущем разделе мы упоминали о том, что в 7-м классе школьникам предлагают построить на бумаге треугольник и три его медианы, убедиться в том, что медианы пересекаются в одной точке, а затем найти отношение бо́льшей части медианы к меньшей. Эксперимент отнюдь не сложен, и школьники с лёгкостью получают нужные утверждения. Правда, доказательство откладывается до 8-го класса [1, c. 33–34], но это даже хорошо, т.к. даёт повод вернуться к эксперименту непосредственно перед доказательством.
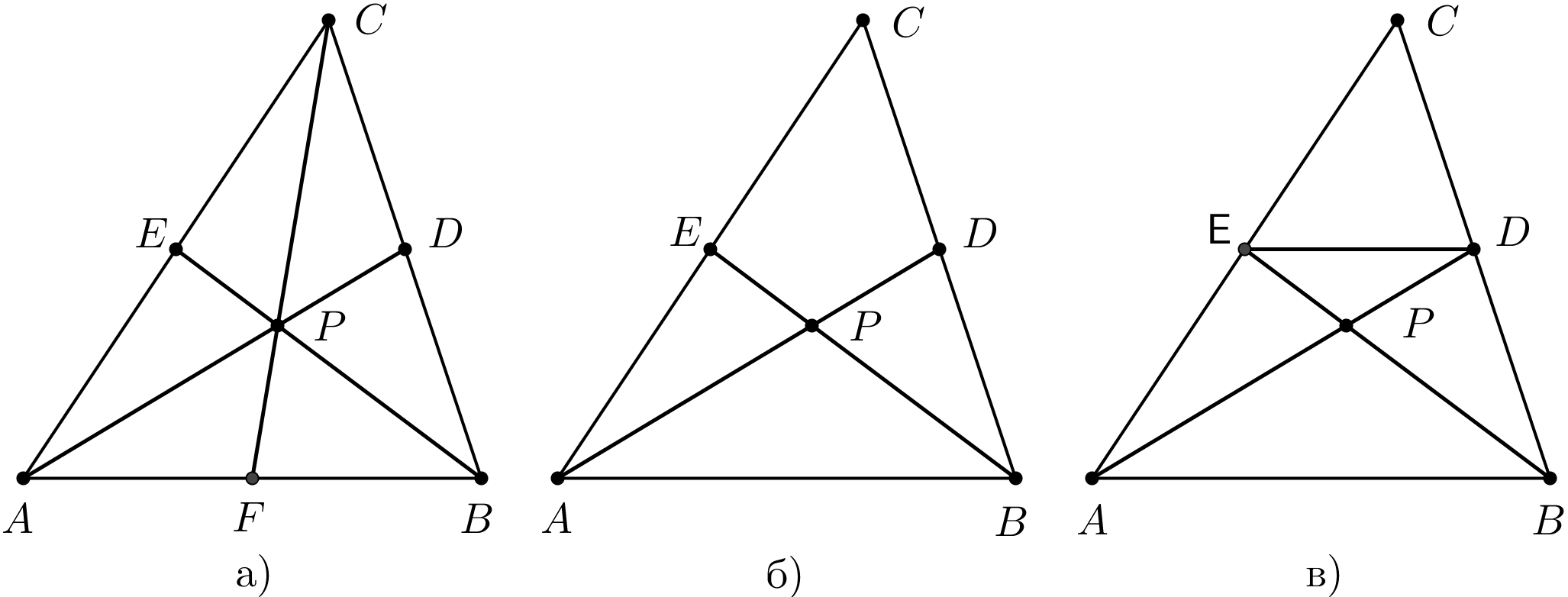
При повторном эксперименте естественно использовать инструмент более точный, чем карандаш, линейка и циркуль, например, интерактивную математическую среду GeoGebra. Вот здесь школьники встречаются с неожиданным обстоятельством: для одних треугольников искомое отношение равно в точности 2:1, а для других треугольников это не совсем так! Двигая, например, одну из вершин с помощью инструмента Перемещать, нетрудно найти треугольник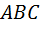 
(рис. 18а), у которого 
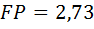, а 
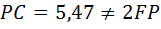. Получается, что
|
|
|
Рис. 18. Медианы треугольника
однотипные эксперименты, осуществляемые с разной точностью, дают различные результаты. Получается, что более точный инструмент делает ненадёжной исходную гипотезу, такую простую и естественную на первый взгляд. Хуже того: неравенство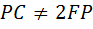 
может встретиться при любой точности округления, доступной компьютеру. В силу этого представляется затруднительным или невозможным разрешить это противоречие с помощью других экспериментов, поскольку предел точности, предоставляемый компьютером, уже достигнут. В этих условиях единственным средством для снятия противоречия между двумя экспериментами является дедуктивное доказательство, для которого придётся провести предварительный теоретический анализ.
Приступая к теоретическому анализу, заметим, что на готовом чертеже медианы треугольника выглядят вполне «равноправными» в том смысле, что каждая из них проходит через точку пересечения двух других. В то же время, очевидно, что во временно́м отношении они не равноправны, потому что сначала мы проводим первую медиану (например,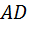 
), затем вторую медиану 
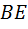, и только потом третью медиану 
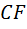. В этой связи было бы естественным сначала проанализировать взаимное расположение первых двух медиан (вновь «дежурный» вопрос!), и лишь затем анализировать положение третьей медианы. Сформулируем наш вопрос следующим образом: «Через какую точку первой медианы 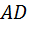проходит вторая медиана ?»
|
|
|
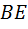Пусть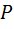 
– точка пересечения медиан 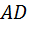и 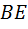(рис. 18б). Выше была высказана гипотеза о том, что 
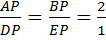. Да, эта гипотеза ненадёжна, но другой гипотезы у нас нет. Попытаемся проверить её истинность.
Очевидно, что пропорциональность четырёх отрезков может быть связана с подобием треугольников, однако на рис. 18б нет подобных треугольников! Для их построения проведём отрезок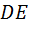 
(рис. 18в).
Дальнейшие рассуждения являются стандартными и весьма лаконичными [1, c. 146]. Из свойств средней линии 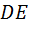вытекает, что 
, причем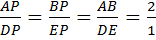 
. Получается, что вторая медиана проходит через такую точку 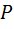первой медианы, которая делит её в отношении 2:1, считая от вершины. При этом сама вторая медиана делится точкой 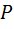в таком же отношении.
|
|
|
Анализируя теперь взаимное расположение первой и третьей медиан, получим, что третья медиана проходит через ту же самую точку 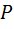и делится ею в том же отношении, что и доказывает теорему.
3. Возвратимся к началу рассмотренного сценария и воспроизведём его общую структуру. При этом выделим курсивом те его элементы, которые не поддаются формализации. По нашему мнению, именно наличие неформализуемых элементов сценария превращает его в модель исследовательской деятельности.
1) Проводится эксперимент, который порождает гипотезу.
2) Проводится уточняющий эксперимент, который делает гипотезу ненадёжной. Противоречие между результатами экспериментов порождает потребность в его устранении. Естественный способ снятия противоречия – это дедуктивное обоснование истинности гипотезы.
3) Делается наблюдение о временно́м неравноправии медиан, которое даёт основание для упрощения конфигурации.
4) Исследование конфигурации из трёх медиан сводится к более простому исследованию конфигурации из двух медиан. При этом вопрос об их взаимном расположении приобретает специальную форму.
|
|
|
5) Приводится аналитическое рассуждение о целесообразности использования подобных треугольников, а затем строятся подобные треугольники.
6) Проводится стандартное доказательство из школьного учебника математики.
Увеличим уровень схематизации нашего сценария. Выписав с этой целью ключевые слова из пунктов 1–6, получим последовательность из 11-ти (!) пунктов: э ксперимент → гипотеза → уточняющий эксперимент → противоречие → потребность в снятии противоречия → дедуктивное обоснование истинности → наблюдение о «неравноправии» медиан → редукция → аналитическое рассуждение → дополнительное построение → формальное доказательство.
Итак, изучение несложной теоремы школьного курса математики можно организовать так, что в нем будут присутствовать многие важные элементы исследовательской деятельности. С нашей точки зрения, подобные сценарии следует использовать целенаправленно и регулярно. Разумеется, и тут мы повторимся, частота их использования должна учитывать конкретные педагогические условия.
4. Обсудим вопрос об отношении к результатам измерений в области физики и в области математики.
Выше уже говорилось о том, что скорость света неоднократно оценивалась или измерялась разными учёными. Первые оценки дали результаты 220000 км/сек (1676 г.) и 308000 км/сек (1728 г.). Прямые измерения также давали разные результаты: 313000 км/сек (1849 г.), 298000 км/сек (1862 г.), 299796 км/сек (1926 г) и др.
Здесь следует отметить одно интересное, но мало обсуждаемое обстоятельство: в определённом, весьма специфическом, смысле значение скорости света не является важным для физиков! Действительно, скорость света такова, какова она есть, и забота исследователей состоит в максимальной точности измерений, а не в том значении, которое получится в результате «правильных», «хороших», точных измерений.
В отличие от исследователей в области физики, для школьника-исследователя важными оказываются не только точность измерений, но и собственно результат измерений. Действительно, если при всех измерениях бо́льшая часть медианы вдвое длиннее меньшей части, то школьник (возраст которого весьма мал!) имеет достаточные основания для выдвижения гипотезы о соотношении частей. Если же при различных измерениях получаются разные результаты, то основания для выдвижения гипотезы «размываются» и становятся ненадёжными. К счастью, эти основания не исчезают бесследно, а дедуктивные рассуждения спасают ситуацию.
В заключение приведём современные данные о скорости света: 299792458 м/сек при абсолютной погрешности 1,2 м/сек. Оценив относительную погрешность в процентах, мы увидим, что проделанное измерение является грандиозным научным достижением, свидетельством величия человеческого духа.
Дата добавления: 2019-09-13; просмотров: 359; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!