ЭЛЕМЕНТЫ ИССЛЕДОВАТЕЛЬСКОЙ ДЕЯТЕЛЬНОСТИ
В ОСНОВНОЙ ШКОЛЕ
Что значит преподавать? – Это значит систематически побуждать учащихся к собственным открытиям.
Г. Спенсер
В главе показано, что программа основной школы позволяет естественным образом ввести в её изучение элементы деятельности математика: постановку вопросов, а значит и решение вытекающих из них задач; первичное обнаружение новых утверждений, которые поначалу существуют в виде гипотез; проверку истинности утверждений-гипотез или, что то же самое, доказательство новых теорем; изобретение определений… Деятельность математика многогранна и не поддаётся полному охвату.
Элементы исследовательской деятельности
Как фактор освоения базового курса математики
Мы начнём с первичного, но отнюдь не простейшего, – с постановки вопросов. Уже говорилось о том, что в начальной школе математический материал осваивается преимущественно эмпирическими методами с элементами теории. В седьмом классе перед школьником начинает разворачиваться безбрежное море теоретического знания. Естественно, что человеку нужны ориентиры, которые, однажды возникнув, будут помогать ему на протяжении всего процесса обучения. Такие ориентиры могут принимать самые разнообразные формы. Например, они могут принимать вид постоянно повторяющихся вопросов, или часто встречающихся конфигураций, или регулярно используемых методов, или полезных эвристических приёмов… Для нас важно, что эти ориентиры, обнаруженные математиками древности, могут помочь современному школьнику повторить в ускоренном виде путь построения геометрии. Сосредоточимся на некоторых из этих ориентиров и попытаемся продемонстрировать их педагогическую значимость.
|
|
|
Вопрос о конфигурации[12]. Геометрия неявно присутствует в жизни человека задолго до того, как он начал её систематическое изучение. К ней приводят простейшие вопросы. Далеко ли от дома до школы? Проходит ли Транссибирская магистраль через Ярославль и Кострому? Находятся ли города Киржач и Зарайск в Московской области? Оказывается, что от дома до школы недалеко, примерно километр. По карте видно, что Транссиб проходит через Ярославль и не проходит через Кострому. По ней же видно, что Киржач не находится в Московской области, а Зарайск находится, хотя Киржач примерно в полтора раза ближе к Москве, чем Зарайск. Во всех этих случаях речь идёт о взаимном расположении геометрических объектов: двух точек (двух зданий), точки и линии (город и дорога), точки и плоской фигуры (город и область).
Игру в объекты можно естественным образом продолжить на первых уроках геометрии. Представим себе двух людей с завязанными глазами, которые рисуют геометрические фигуры на одном листе бумаги, один красным карандашом, а другой – синим. Если каждый из них нарисует по точке, то они, скорее всего, не совпадут, но могут и совпасть. Если один из людей нарисует прямую, а другой точку, то точка, скорее всего, не попадёт на линию, но может и оказаться на ней. Если игроки нарисуют прямую линию каждый, то разноцветные прямые, скорее всего, пересекутся, но могут и не пересечься. Более того, они могут и совпасть. Во всех этих случаях речь идёт о взаимном расположении геометрических объектов: двух точек, точки и прямой, двух прямых.
|
|
|
Итак, один из фундаментальных вопросов геометрии звучит следующим образом: «Каково взаимное расположение двух геометрических объектов?»
Приведём примеры ситуаций, в которых постановка нашего вопроса вполне естественна. Попытаемся также выявить те моменты изучения геометрии, когда сама постановка этого вопроса оказывает значимое развивающее воздействие.
1) Каково взаимное расположение основания равнобедренного треугольника И биссектрисы противолежащего угла? После некоторых рассуждений выясняется следующее. Во-первых, биссектриса проходит через середину основания, то есть является медианой. Во-вторых, она пересекает основание под прямым углом, то есть является его высотой.
|
|
|
2) Каково взаимное расположение стороны треугольника И средней линии, проведённой через середины двух других сторон? После некоторых рассуждений оказывается, что эти отрезки параллельны.
3) Каково взаимное расположение трёх медиан (биссектрис, высот) треугольника? Оказывается, что три медианы (биссектрисы, высоты) проходят через одну точку.
Уже эти простейшие примеры выявляют ряд поучительных моментов.
Во-первых, благодаря вопросам объекты изучения оказываются чётко определёнными, а это облегчает школьникам понимание ситуации.
Во-вторых, изучение ситуации начинается с постановки вопроса, как это обычно и происходит в «высокой» науке.
В-третьих, окончательный результат математического изучения нуждается в словесном выражении, и это словесное выражение становится формулировкой теоремы. Вновь на уроке все происходит примерно так, как это имеет место в математике.
В-четвертых, теорема перестаёт быть неким утверждением, пришедшим к школьнику извне (то есть неизвестно откуда) и требующим (по неизвестным причинам) своего осмысления, а превращается в продукт его личной деятельности. Заметим, что сам переход от математических рассуждений к словесной формулировке результата является отдельным интеллектуальным действием междисциплинарного характера, которое подчас оказывается непростым.
|
|
|
В-пятых, благодаря первичному характеру вопроса и вторичному характеру формулировки теоремы учитель и ученик приобретают определённую свободу действий на пути от вопроса к ответу. Например, ответ на вопрос 1 может быть получен путём теоретических рассуждений, как это сделано, например, в учебнике [1, c. 35]. В то же время можно спланировать эксперимент в интерактивной математической среде: построить произвольный треугольник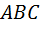 
, провести биссектрису 
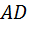, измерить отрезки 
, 
, 
и 
, а затем перемещать вершину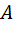 
, стараясь добиться такого ее положения, чтобы отрезки и приобрели равную длину. Если это удастся сделать (во многих случаях это отнюдь не легко), то равенство или примерное равенство отрезков и подскажет верный ответ. Подчеркнём, что мы не оцениваем сейчас достоинства или целесообразность каждого из двух подходов. Для нас важно, что участники педагогического процесса имеют свободу выбора.
Итак, мы привели некоторые аргументы в пользу того, что освоение новой теоремы должно начинаться с постановки вопроса. Интересно, что эти аргументы имеют разную природу. Так, первый и четвёртый аргумент носят по преимуществу психологический характер, второй и третий относятся к свойствам математики как науки, а последний в значительной мере относится к педагогике. С нашей точки зрения, разнотипность аргументов в пользу одного утверждения усиливает их значимость.
Рис. 14. Каково взаимное расположение треугольников?
Очевидно, что для разных этапов обучения характерны разные способы использования вопросов о конфигурации. Поначалу такие вопросы ставятся преимущественно учителем. Для учеников они служат образцами постановки математических вопросов, к которым они со временем привыкают и научаются формулировать. Постепенно школьники вовлекаются в процесс постановки вопросов и, как нам кажется, приобретают определённый опыт в их постановке.
В этой связи заметим, что вопрос о взаимном расположении геометрических фигур может оказаться достаточно сложным. Например, хорошо известно, что три средние линии треугольника разбивают его на четыре конгруэнтных (равных) треугольника. Каково же взаимное расположение исходного треугольника и каждого из четырёх треугольников, изображённых на рис. 14? Ответ звучит неожиданно для школьников, да и для многих студентов. Оказывается, что все треугольники гомотетичны исходному треугольнику 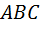, правда, при этом центры гомотетий и коэффициенты гомотетий могут различаться. Так, треугольник 
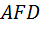гомотетичен треугольнику 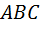с центром 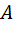и коэффициентом 
, а треугольник 
гомотетичен треугольнику 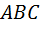с центром в точке пересечения медиан и коэффициентом 
.
В заключение отметим следующее: в книге [1] ответ на вопрос 3 формулируется в начале 7-го класса, а доказательство истинности ответа приводится только в 8-м. Тем самым в учебник проникает типичная для науки ситуация, когда формулировка утверждения и его доказательство отделены друг от друга неким промежутком времени, порой весьма длительным.
Вопрос о пропорции[13]. В начальной школе дети осваивают метод сравнения двух различных величин. Он имеет вид двух разнотипных, но в равной мере приемлемых вопросов: «на сколько единиц больше?» и «во сколько раз больше?». Интересно, что в геометрии равноправие вопросов исчезает!
Рис.15. Какой вопрос уместнее?
Для иллюстрации нарисуем на клетчатой бумаге треугольник 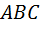и проведем его среднюю линию 
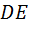(рис. 15). Если спросить, на сколько клеток средняя линия короче основания, то легко получить очевидный ответ – на три клетки. Если задать тот же вопрос о треугольнике 
и его средней линии 
, то ответ будет другим – на шесть клеток. Между тем, треугольники имеют совершенно одинаковую форму, так что вопрос «на сколько единиц больше?» никак не характеризует соотношение между стороной треугольника и его средней линией. В отличие от первого вопроса, второй вопрос «во сколько раз больше?» в обоих случаях имеет один ответ – в два раза больше. Очевидно, что один и тот же ответ для двух фигур одинаковой формы отражает важное соотношение между двумя отрезками.
Итак, ещё один из фундаментальных вопросов геометрии звучит следующим образом: «Во сколько раз одна геометрическая фигура больше другой?»
Приведём примеры других ситуаций, в которых постановка нашего вопроса вполне естественна. Попытаемся показать, что сама постановка вопроса зачастую оказывает значимое развивающее воздействие.
1) Мы уже говорили о том, что три медианы треугольника имеют общую точку. Очевидно, что эта точка делит каждую медиану на две части, бо́льшую и меньшую. Во сколько раз одна часть больше другой? После некоторых рассуждений оказывается, что в два раза. Так школьник узнает, что визуальные наблюдения могут иметь теоретические объяснения.
2) Мы уже говорили о том, что три биссектрисы треугольника имеют общую точку. Очевидно, что эта точка делит каждую биссектрису на две части, бо́льшую и меньшую. Во сколько раз одна часть больше другой? После некоторых действий (например, измерений и вычислений) оказывается, что вопрос не имеет смысла, потому что отношение отрезков является различным для разных биссектрис, а кроме того, меняется в процессе варьирования треугольника. Так школьник узнает, что визуальные наблюдения могут быть обманчивы и, следовательно, их справедливость нуждается в теоретическом объяснении.
3) Если построить вписанный и центральный углы, опирающиеся на одну и ту же дугу окружности, то нетрудно заметить, что центральный угол больше вписанного. Во сколько раз один угол больше другого? В статье [43] описаны противоречивые результаты компьютерного эксперимента. Так, для многих углов оказывается, что центральный угол ровно вдвое больше вписанного, поэтому можно счесть подмеченное обстоятельство закономерностью. Однако для других углов это не совсем так, например 
. (Здесь 
– это центральный угол, опирающийся на дугу 
, а 
– это вписанный угол.) Конечно, разница между центральным углом и удвоенным вписанным углом невелика и составляет одну сотую градуса, но она существует. Увеличение точности вычислений не приводит к разрешению противоречия, потому что при каждой точности встречаются противоречащие друг другу результаты измерений. Так школьник узнает, что буквалистское истолкование результатов компьютерных экспериментов может приводить к парадоксальным результатам и, в силу этого, малополезно. Он узнает, что инструментом разрешения противоречия между показаниями двух экспериментов является дедуктивное доказательство.
Выше мы привели несколько аргументов в пользу утверждения о том, что своевременная постановка вопросов о конфигурации придаёт изучению геометрии исследовательски-ориентированный характер. Можно утверждать, что эти же аргументы с полным основанием применимы к вопросам о пропорции.
Фундаментальные конфигурации. Одной из простейших фигур курса геометрии является отрезок. Внутренние точки отрезка обычно воспринимаются школьниками как «равноправные», как нечто «безличное», не обладающее какими-либо интересными индивидуальными свойствами. Покажем, что это не так, что есть на нем одна точка, особое положение которой предопределяет многие свойства геометрических фигур. Мы имеем в виду середину отрезка. Действительно, вокруг этого понятия разворачивается настоящий «геометрический детектив», который мы попытаемся описать.
Завязкой «детектива» служат две простые теоремы. Во-первых, если вершину равнобедренного треугольника соединить с серединой основания, то построенный отрезок окажется и биссектрисой угла, и высотой, и осью симметрии. Во-вторых, множеством точек, равноудалённых от концов отрезка, является серединный перпендикуляр к нему.
Треугольник имеет три стороны и, следовательно, три середины. С ними ребёнок может «играть» весьма длительное время.
Если соединить две середины их трёх, то получим отрезок, фигурирующий в теореме о средней линии треугольника.
Если соединить три середины последовательно, то треугольник разобьётся на четыре равных треугольника, подобных исходному.
Если каждую из середин соединить с противоположной вершиной, то получим теорему о медианах треугольника. При этом треугольник разобьётся на шесть треугольников, которые, и это удивительно, равновелики.
Если через середины всех сторон треугольника провести перпендикуляры к сторонам, то окажется, что они пересекаются в одной точке, которая равноудалена от вершин треугольника.
Если через середины трёх сторон треугольника провести окружность, то поначалу ничего не удаётся заметить. Однако если дополнительно провести высоты, то основания высот совпадут с точками пересечения окружности и сторон (или их продолжений), а сама окружность пройдёт через середины отрезков между ортоцентром и вершиной. Так получается, что из девяти замечательных точек окружности Эйлера шесть являются серединами некоторых отрезков.
Четырёхугольник имеет четыре стороны и, следовательно, четыре середины. И с этими серединами можно долго «играть».
Если последовательно соединить середины сторон четырёхугольника, то получится параллелограмм.
Если соединить середины противоположных сторон, то четырёхугольник разобьётся на четыре четырёхугольника. Оказывается, что сумма площадей двух «диагональных» четырёхугольников, единственной общей точкой которых является вершина, равна сумме площадей двух других диагональных четырёхугольников. (В книге [5, c. 26] это утверждение носит красивое жаргонное название «1-я теорема о бабочках».)
Очевидно, что диагональ четырёхугольника делит его на два треугольника. Оказывается, они равновелики тогда и только тогда, когда эта диагональ проходит через середину второй диагонали.
Если четырёхугольник оказывается трапецией, то её средняя линия играет особую роль.
Если четырёхугольник оказывается параллелограммом, то середины диагоналей совпадают с точкой их пересечения.
В треугольной пирамиде можно проделать следующие построения: найти середину ребра, затем середину скрещивающегося ребра, а затем середину отрезка, соединяющего найденные точки. Оказывается, что результат не зависит от того ребра, с которого начаты построения. (Автор назвал бы это утверждение «теоремой о многих серединах».)
Итак, «детектив» прочитан, хотя и может иметь продолжение. Он означает, что середина отрезка участвует во многих теоремах курса геометрии, которые изучаются в течение целого ряда лет. Естественно зафиксировать это понятие в качестве ориентира в море геометрических теорем в качестве одного из опорных понятий, которое может помочь школьнику осмысливать изучаемое.
Эристики. Очевидно, что освоение математики невозможно без решения большого количества задач. В свою очередь, решение задач окажется малопродуктивным, если учащийся не будет осваивать, накапливать, систематизировать и применять полезные эвристические приёмы. Практика преподавания геометрии накопила большое количество таких приёмов. Например, в справочнике [25, c. 209–222] приведено 11 приёмов доказательства равенства двух отрезков, 11 приёмов доказательства параллельности прямых, 13 приёмов доказательства перпендикулярности прямых, 10 приёмов доказательства принадлежности трёх точек одной прямой. Освоение всего этого богатства может показаться школьнику непосильной и потому неинтересной задачей. Впрочем, такое впечатление можно исправить, если сознательно попытаться запустить механизм положительной обратной связи: чувства исследователя, хотя бы минимальные, заставят начать освоение эвристических приёмов, а успешное применение приёмов будет стимулировать исследовательское поведение.
В заключение отметим, что наш список продуктивных вопросов отнюдь не является полным, равно как не являются полными ни список полезных конфигураций, ни список эвристических приёмов. Мы лишь хотим обратить внимание на необходимость их изначального существования и последующего пополнения. Именно они формируют исследовательское поведение школьников и способствуют превращению преподавания в исследовательски ориентированное.
Дата добавления: 2019-09-13; просмотров: 316; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!