ПРИМЕРЫ РЕШЕНИЯ ИНДИВИДУАЛЬНЫХ заданий
Задача 1.В плоскости α(а∩в) через точку А провести горизонталь h и через точку В-фронталь f (рис. 229).
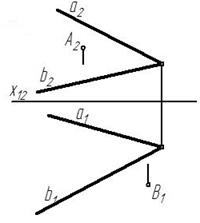
Рис. 229
Прямая принадлежит плоскости, если она имеет с ней две общие точки или имеет одну общую точку и параллельна прямой этой плоскости.
Находим фронтальную проекцию точки А. Для этого через горизонтальную проекцию А1 точки А проводим горизонтальную проекцию11-21 произвольной прямой 1-2, принадлежащей заданной плоскости α(а∩в). На фронтальной проекции 12-22 прямой 1-2 отмечаем А2. Через фронтальную проекцию А2 точки А проводим параллельно оси х12 фронтальную проекцию h2 горизонтали h. Затем через точки 31 и А1 проводим горизонтальную проекцию горизонтали h1 (рис. 230, а).
Находим горизонтальную проекцию точки В. Для этого проводим фронтальную проекцию 42-52 произвольной прямой 4-5, принадлежащей заданной плоскости α(а∩в). На горизонтальной проекции 41-51 прямой 4-5 отмечаем В1. Через горизонтальную проекцию В1 точки В проводим параллельно оси х12 горизонтальную проекцию f1 фронтали f. Затем через точки В2 и 62 проводим фронтальную проекцию фронтали f2 (рис. 230, б).
а) б)
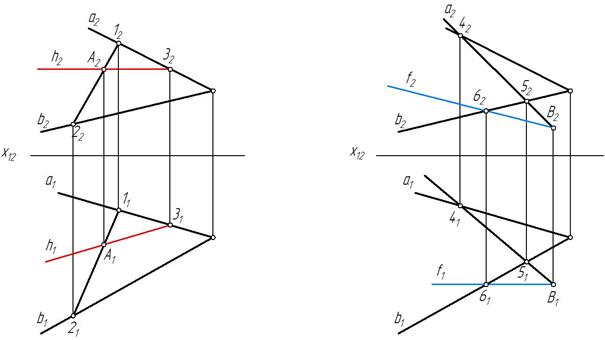
Рис. 230
Задача 2.
Пример 1. Построить фронтальную проекцию треугольника АВС, принадлежащего плоскости α(f∩h) (рис. 231).
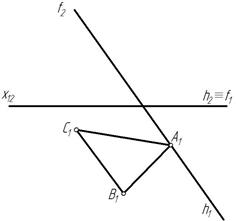
Рис. 231
Точка принадлежит плоскости, если она находится на прямой, принадлежащей этой плоскости. В качестве прямых, принадлежащих плоскости, удобно воспользоваться главными линиями плоскости – горизонталью h или фронталью f.
|
|
|
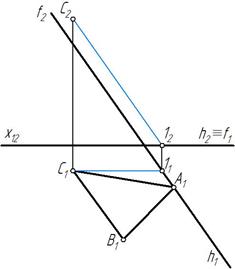
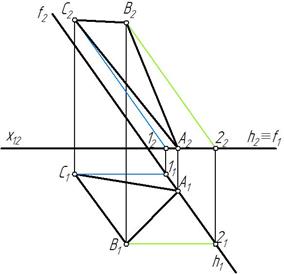
Рис. 232 Рис. 233
Строим фронтальную проекцию С2 точки С. Для этого через горизонтальную проекцию С1 проводим горизонтальную проекцию фронтали параллельно оси х 12. Строим фронтальную проекцию фронтали параллельно f 2 и отмечаем на ней фронтальную проекцию С2 (рис. 232).
Аналогично строим фронтальную проекцию В2. Строим фронтальную проекцию точки А 2 на h2. Соединяем А2В2С2 и получаем недостающую фронтальную проекцию треугольника АВС (рис. 233).
Пример 2. Построить фронтальную проекцию треугольника АВС, принадлежащего плоскости α(ΔМ NK) (рис. 234).
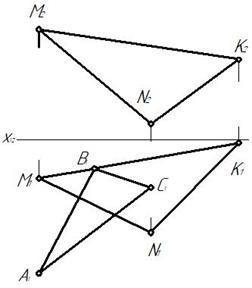
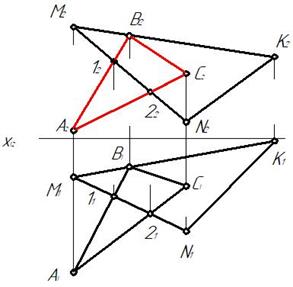
Рис. 234 Рис. 235
Точка В принадлежит прямой М K, отмечаем фронтальную проекцию В2 на фронтальной проекции прямой М K. Затем отмечаем точку 11 на пересечении горизонтальных проекций прямых AB и MN. По линии связи отмечаем 12 на M2N2 и через точки В2 и 12 проводим прямую и на ней отмечаем М2. Построение точки С2 понятно из чертежа (рис. 235)
|
|
|
Задача 3.
Пример 1. Найти точку пересечения прямой l плоскостью α(а‖b) (рис. 236).
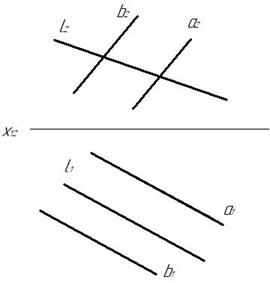
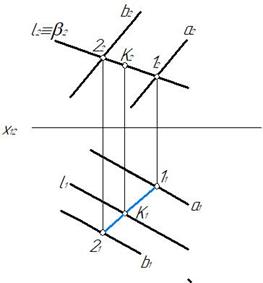
Рис. 236 Рис. 237
Плоскость α, заданная параллельными прямыми, является плоскостью общего положения. Проводим через прямую l вспомогательную плоскость β^П2. Строим линию пересечения плоскостей заданной α и вспомогательной β – это будет прямая 1-2. В месте пересечения горизонтальных проекций l 1 и 1121 отмечаем горизонтальную проекцию K1. Фронтальную проекцию K2 точки K находим по принадлежности точки K прямой l (рис. 237). Видимость прямой не отмечаем.
Пример 2. Найти точку пересечения прямой l плоскостью α(m ∩ n) (рис. 238).

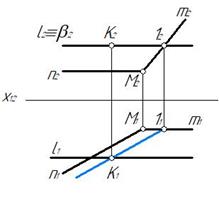
Рис. 238 Рис. 239
Плоскость α(m∩n) является плоскостью общего положения. Проведем через прямую l вспомогательную плоскость β‖П1. Линией пересечения, заданной α и вспомогательной плоскости β будет горизонталь, проведенная параллельно горизонтали n. Дальнейшее построение понятно из чертежа (рис. 239).
Задача 4. Построить линию пересечения DАВС и DDEF(рис. 240).
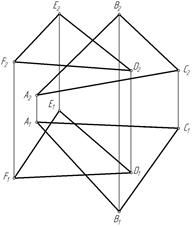
Рис.
240
Чтобы построить линию пересечения двух треугольников, необходимо найти точки пересечения двух прямых, принадлежащих одной из плоскостей, с другой плоскостью.
|
|
|
Находим точку пересечения стороны АВ с плоскостью ΔDEF. Для этого через прямую АВ проводим вспомогательную фронтально-проецирующую плоскость α. Строим линию 1-2 пересечения вспомогательной плоскости α с ΔDEF и отмечаем на пересечении с АВ искомую точку М (рис. 241).
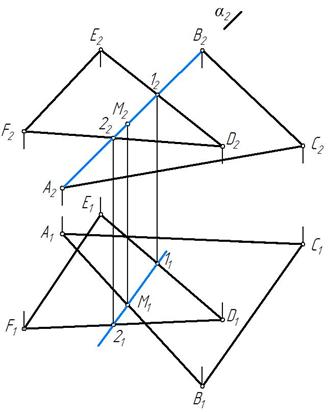
Рис. 241
Аналогичным образом, через прямую DE проводим фронтально-проецирующую плоскость β. Строим линию 3-4 пересечения плоскости β с ΔАВС и отмечаем на пересечении с DE искомую точку N (рис. 242).
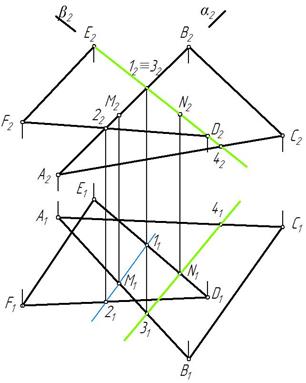
Рис. 242
Прямая МN искомой линии пересечения плоскостей двух треугольников построена на рис.243.
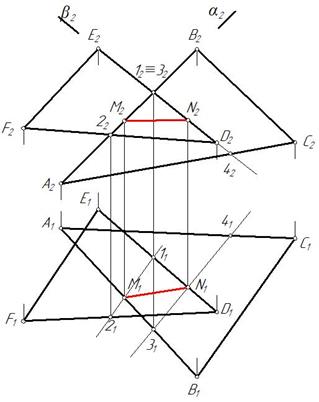
Рис. 243
Определяем видимость треугольников на П2. Для этого на П2 сравниваем видимость скрещивающихся прямых АВ и D Е. Отметим точки 3∈АВ, 1∈D Е. Горизонтальная проекция 31 находится перед 11 (направление взгляда А). Невидимая точка 12 закрыта в скобки (рис. 244). Следовательно, прямая А2В2 видима до М2, а часть прямой А2В2 закрывается плоскостью DEF.
Определяем видимость треугольников на П1. Для этого сравниваем видимость скрещивающихся прямых АВ и ЕF. Отмечаем точки 5∈АВ, 6∈EF. Фронтальная проекция 62 находится выше 52 (направление взгляда Б). Следовательно, E 1 F 1 видима, а закрывается часть прямой А1В1 до точки М1 (рис. 244).
|
|
|
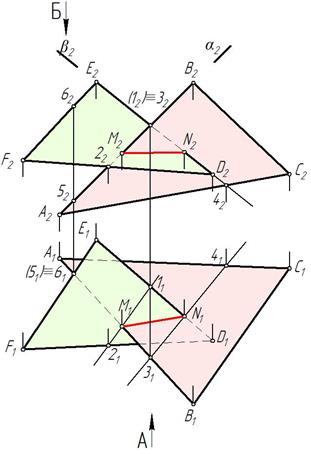
Рис. 244
Задача 5.
Пример 1. Определить расстояние от точки А до прямой l (рис. 245).
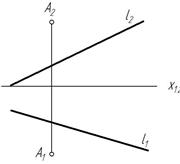
Рис. 245
Расстояние от точки до прямой определяется длиной отрезка перпендикуляра, опущенного из точки на прямую.
На эпюре проекции перпендикуляра к прямой можно построить, если прямая параллельна плоскости проекций. Поэтому сначала строим дополнительную ортогональную проекцию прямой и точки А на плоскости П4, параллельной прямой l и перпендикулярной к П1. При этом ось х14 параллельна l 1 . Для построения дополнительной проекции прямой l на ней отмечены точки 1 и 2 (рис. 246).
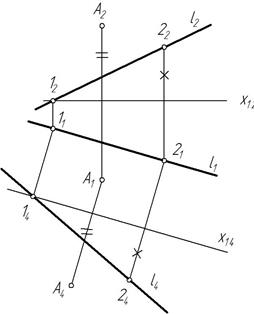
Рис. 246
2. Проводим дополнительную проекцию А4 K 4 перпендикуляра (А4 K 4 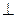 l 4), а затем строим горизонтальную проекцию А 1 K 1 . Построена также и фронтальная А 2 K 2 проекция перпендикуляра АK (рис. 247).
l 4), а затем строим горизонтальную проекцию А 1 K 1 . Построена также и фронтальная А 2 K 2 проекция перпендикуляра АK (рис. 247).
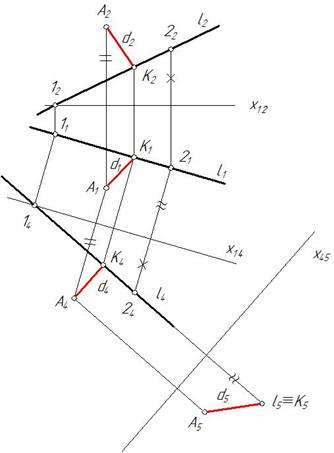
Рис. 247
Отрезок АK – общего положения. По двум данным проекциям отрезка АK (А 1 K 1 и А 4 K 4) находим его длину, построив дополнительную ортогональную проекцию отрезка на плоскости П5, параллельной АK и перпендикулярной к П4. Ось х45 параллельна А4K4 (рис. 247).
Аналогично можно определить расстояние между двумя параллельными прямыми. Для этого возьмем на одной прямой любую точку и найдем расстояние от этой точки до второй прямой.
Пример 2. Определить расстояние от точки А до плоскости α (f∩h) (рис. 248).
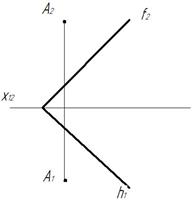
Рис. 248
Расстоянием от точки до плоскости является длина отрезка перпендикуляра, опущенного из точки на плоскость.
Если плоскость является проецирующей, то перпендикуляр к ней параллелен плоскости проекций и длина проекции его отрезка на этой плоскости проекций равна искомому расстоянию. Исходя из этого построим дополнительную ортогональную проекцию плоскости α и точки А на плоскости, перпендикулярной к плоскости α и к плоскости П1.
Плоскость П4 будет перпендикулярна к плоскости α, если она перпендикулярна к горизонтали этой плоскости. При этом ось х14 перпендикулярна к горизонтальной проекции h 1 горизонтали h плоскости α. Дополнительной ортогональной проекцией плоскости α на плоскость П4 является прямая f4. Для ее построения отметили произвольную точку 1 и построили ее дополнительную проекцию 14.
Из точки А4 опускаем перпендикуляр А4 K 4 на прямую f4. Длина отрезка А4 K 4 равна расстоянию от точки А до плоскости α(ΔBCD).
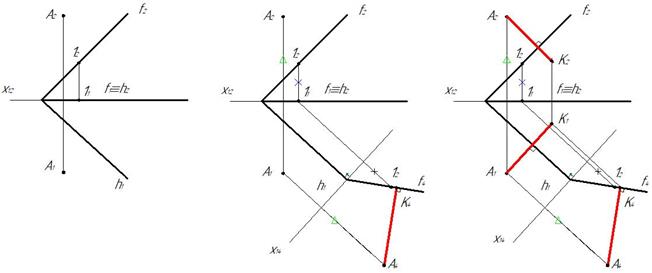
Рис. 249
Построим проекции отрезка АК. Горизонтальная проекция А1 K 1 параллельна оси х14, так как отрезок АK параллелен плоскости П4, и перпендикулярна к горизонтальной проекции h 1 горизонтали h плоскости α. Фронтальную проекцию А2 K 2 строим перпендикулярно фронтальной проекции фронтали f2. Поэтапное решение показано на (рис. 249).
На основании решения рассмотренной задачи можно определить расстояние между параллельными прямой и плоскостью, между двумя параллельными плоскостями.
Задача 6.Определить натуральную величину угла между двумя пересекающимися прямыми (рис. 250).
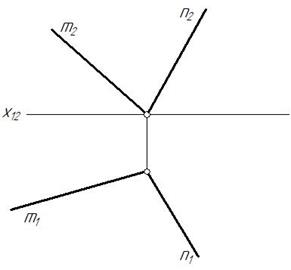
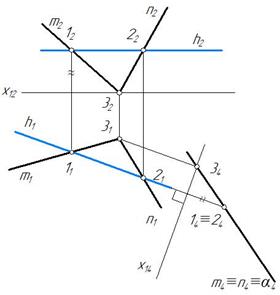
Рис. 250 Рис. 251
Угол между двумя пересекающимися прямыми спроецируется без искажения на плоскость проекций, параллельную плоскости α(m⋂n). Но сразу выбрать плоскость параллельную плоскости угла и перпендикулярную плоскостям проекций невозможно. Поэтому сначала построим дополнительную ортогональную проекцию плоскости α(m⋂n) на плоскость ей перпендикулярную П4^α(m⋂n) и П4^П1. Для этого в плоскости α(m⋂n) проводим горизонталь h и перпендикулярно ей строим ось х14. Плоскость α спроецируется в прямую линию (рис. 251).
Затем строим дополнительную ортогональную проекцию плоскости α(m⋂n) на плоскость ей параллельную П5‖α(m⋂n) и П5^П4. Ось х45 проведена параллельно α4. Угол между m 5 и n 5 равен искомому углу φ (рис. 252).
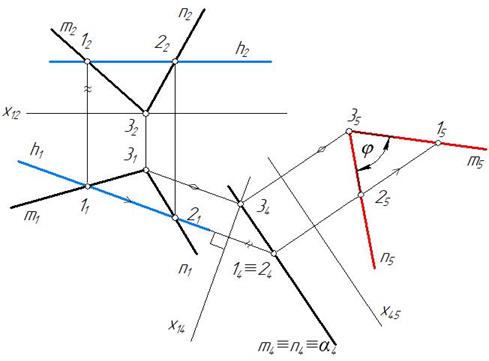
Рис. 252
Задача 7. Построить точки пересечения прямой l с поверхностью призмы. Определить видимость прямой (рис. 253).
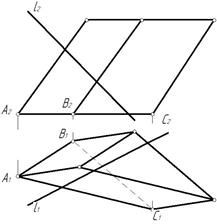
Рис. 253
Через прямую l проводим фронтально-проецирующую плоскость α^П2, l2 ≡ α2. Строим линию пересечения плоскости α с поверхностью призмы. На фронтальной проекции отметим 12, 22, в которых α2 пересекает проекции ребер, а также 32 и 42 на основании. Горизонтальные проекции 11, 21, 31, 41 отмечаем на соответствующих проекциях ребер. Соединяем горизонтальные проекции 11, 21, 31, 41 ломаной линией с учетом видимости. Боковая грань, примыкающая к ребру ВС основания на горизонтальной проекции невидима, так как это ребро невидимо. Следовательно, отрезок 21-41 также не видим (рис. 254).
На пересечении горизонтальной проекции l 1 с горизонтальной проекцией 11-21-31--41 отмечаем горизонтальные проекции M 1 и N 1 точек М и N.
Строим фронтальные проекции M 2 и N 2 на l 2 по линии связи.
Определяем видимость прямой l. Между полученными точками M и N на обеих проекциях прямая l невидима всегда. Горизонтальная проекция l 1 невидима между M 1 N 1 и от N 1 до выхода за очерк призмы, так как горизонтальная проекция N 1 принадлежит невидимой относительно П1 грани ВС.
На П2: точка М находится на грани A С невидимой относительно П2, следовательно, М 2 невидима и фронтальная проекция l 2 невидима до ребра. Точка N принадлежит грани В C, видимой относительно П2, следовательно, фронтальная проекция N 2 видима и фронтальная проекция l 2 от N 2 видима. За очерками призмы прямая l видима (рис. 255).
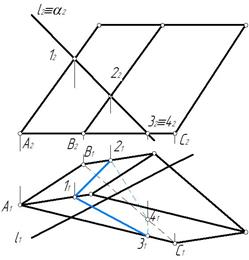
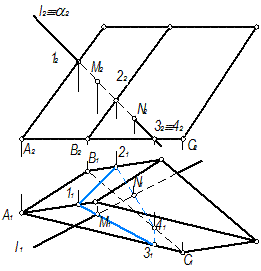
Рис. 254 Рис. 255
Задача 8. Построить точки пересечения прямой l с поверхностью цилиндра. Определить видимость прямой (рис. 256).
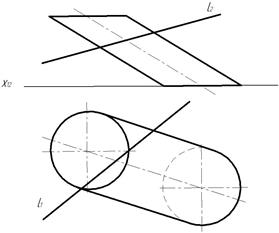
Рис.256
Для нахождения точек пересечения прямой с поверхностью необходимо через прямую провести вспомогательную плоскость такую, чтобы она пересекала поверхность цилиндра по простым линиям. Проведем плоскость, параллельную оси цилиндра. Зададим ее параллельными прямыми. Эта плоскость пересекает заданную поверхность по образующим.
На прямой l возьмем произвольные точки А (А1, А2) и В (В1, В2). Через эти точки проведем прямые а и в, параллельные оси цилиндра.
Строим линию пересечения вспомогательной плоскости с плоскостью основания цилиндра. Это прямая линия α1 (рис. 257).
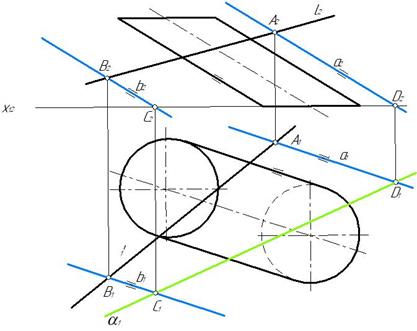
Рис. 257
Строим горизонтальные проекции образующих, которые проходят через горизонтальные проекции 11 и 21 точек 1 и 2 пересечения плоскости α с основанием поверхности цилиндра.
На пресечении горизонтальных проекций образующих и прямой l находим горизонтальныепроекции М1 и N1 искомых точек пересечения М и N, а по ним строим фронтальные проекции М2 и N2 этих точек.
Определяем видимость прямой l. Между полученными точками прямая всегда невидима. Видимость точек М и N определяем по видимости образующих, на которых находятся эти точки (рис. 258).
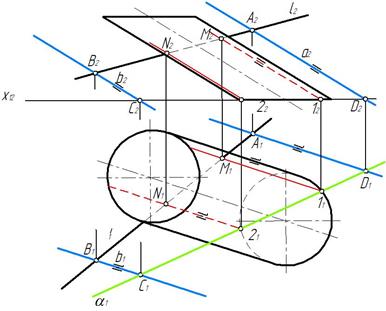
Рис. 258
Задача 9. Построить линию пересечения плоскости δ(f∩h) c поверхностью пирамиды (рис. 259).
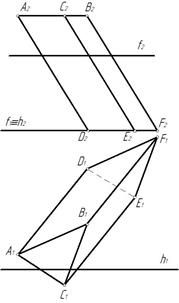
Рис. 259
Линия пересечения в данном случае – замкнутая ломаная линия. Для ее построения необходимо найти точки пересечения ребер призмы с заданной плоскостью.
Чтобы найти точку М, в которой ребро A D призмы пересекает плоскость α(f∩h), через ребро A D проводим вспомогательную плоскость β^П2. Затем строим линию пересечения вспомогательной плоскости с заданной (это прямая 1-2). Прямая 1-2 пересекается с ребром A D в точке М (М1, М2) (рис. 260).
Аналогично определены точки N и L, в которых ребра СЕ, BF пересекают плоскость α(f∩h).
Полученные точки М, N и L соединяем отрезками прямых с учетом видимости. Видимость устанавливаем по видимости граней призмы (рис. 261).
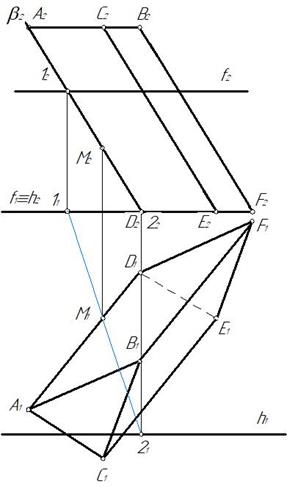
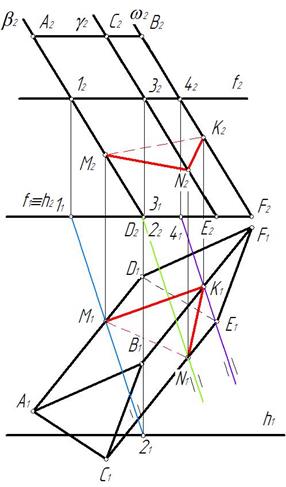
Рис. 260 Рис. 261
Задача 10.
Пример1. Построить линию пересечения плооскости α(f ∩ h ) с цилиндрической поверхностью (рис. 262).
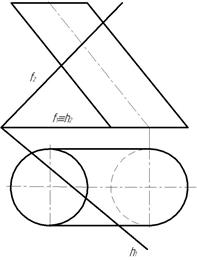
Рис. 262
Линия персечения заданной плоскости α с цилиндрической поверхностью будет эллипс. Для построения линии пересечения найдем ряд ее точек, как точек пересечения образующих поверхности цилиндра сплоскостью.
Строим опорные точки на очерковых образующих (точки А, В, С, D). Для нахождения точки А на очерковой образующей, обозначенной точкой 1, через нее проводим вспомогательную плоскость β^П2. Затем строим линию пересечения вспомогательной плоскости β с заданной плоскостью α(f ∩ h ) – это прямая 2-3. Образующая 1 и прямая 2-3 пересекаются в искомой точке А(А1, А2) (рис. 263).
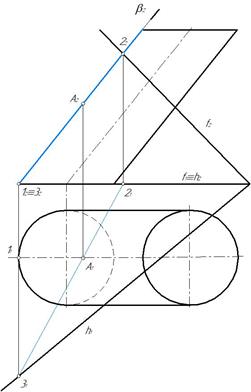
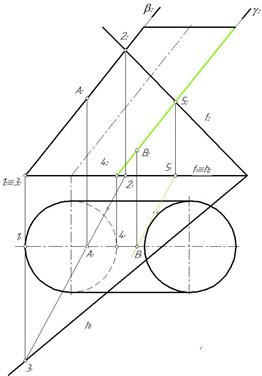
Рис. 263 Рис. 264
Аналогично строим остальные точки линии персечения. На рис. 263 показано построение точки В. При построении горизонтальной проекции линии пересечения вспомогательной плоскости γ с плоскостью α(f ∩ h) пользуемся тем, что фронтальная проекция прямой 2-3 параллельна фронтальной проекции прямой 4-5, значит параллельны и горизонтальные проекции этих прямых. На рис. 265 показано построение точек С и D.
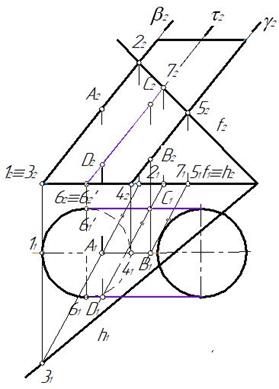
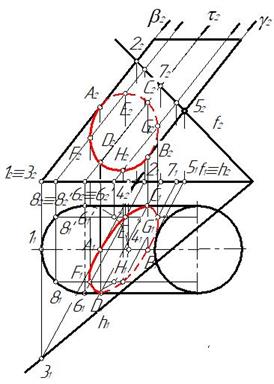
Рис. 265 Рис. 266
Строим также промежуточные точки E, F, G, H на произвольных образующих. Полученные точки соединяем плавной кривой с учетом видимости. Видимость линии пересечения устанавливаем по видимости одной точки, например F, лежащей на образующей 8, которая видима как относительно плоскости проекций П1, так относительно плоскости проекций П2. В точках касания эллипса с очерковыми образующими видимость эллипса изменяется (рис. 266).
Пример 2. Построить линию пересечения конуса с плоскостью α(f ∩ h )(рис. 267.)
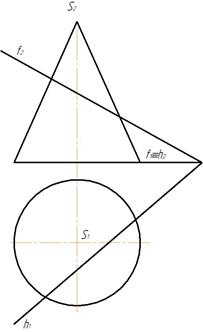
Рис. 267
Заданная плоскость общего положения. Линией пересечения будет часть эллипса, ограниченная прямой. Поскольку основание и горизонталь находятся на горизонтальной плоскости проекций отметим общие точки их пересечения – А и В. Найдем точку пересечения очерковой образующей с заданной плоскостью α. Для этого проводим через точку 1 фронталь в заданной плоскости α . Фронталь пересекает очерковую образующую в точке С (рис. 268)
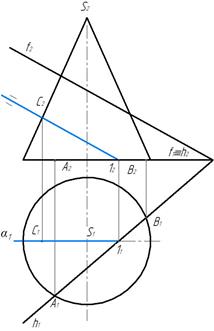
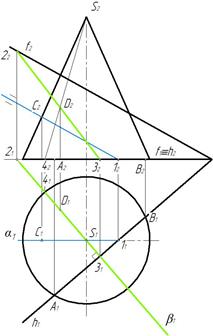
Рис. 268 Рис. 269
Для нахождения самой высокой точки линии пересечения проведем вспомогательную плоскость β перпендикулярную горизонтали h плоскости α .Образующая S 5 в точке D пресекается с прямой 3-4, являющейся линией пресечения плоскостей α и β (рис. 269).
Для нахождения промежуточных точек линии пересечения проведем вспомогательную горизонтальную плоскость γ. Плоскость γ пересекает конус по окружности, а плоскость α по горизонтали,проходящей через точку 6. В месте пересечения горизонтали и окружности отмечаем точки Е и F.
Полученные точки АЕСD FB соединяем с учетом видимости (рис. 270).
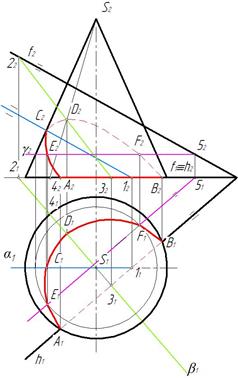
Рис. 270
Задача 11. Построить линию пересечения призмы с конусом (рис. 271).
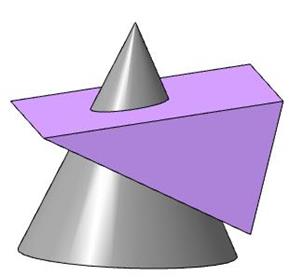
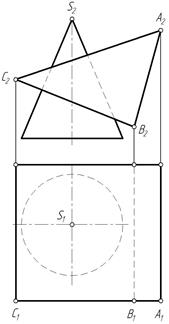
Рис. 271
Поверхность призмы занимает фронтально-проецирующее положение. Грань АВ не пересекает конус.
Грани АС и ВС призмы пересекут конус по эллипсам. Для построения эллипсов надо взять ряд точек на грани и построить их горизонтальные проекции. Точки 1 и 2, 9 и 10 отмечены на очерковых образующих конуса, остальные находятся на окружностях, проведенных на поверхности конуса (рис. 272, 273).
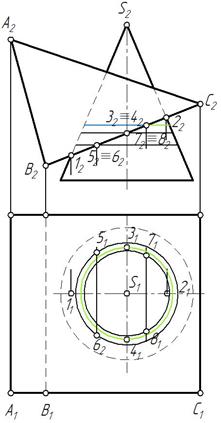
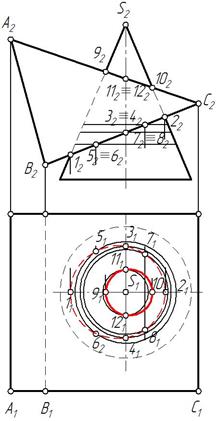
Рис. 272 Рис. 273
Полученные точки соединяем плавными кривыми. Видимость эллипсов определяется видимостью граней. Грань АС видима относительно плоскости проекций П1, следовательно, эллипс 91-111-101-121 видим. Грань призмы ВС невидима относительно плоскости П1, следовательно, эллипс 11-51-31-71-21-81-41-61-11 не видим (рис. 273). Определена также видимость очерков поверхностей.
Задача 12
Пример 1. Построить три проекции выреза на конусе (рис. 274).
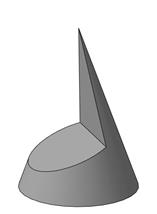
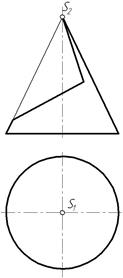
Рис. 274
Вырез произведен двумя фронтально-проецирующими плоскостями. Плоскость α проходит через вершину конуса и пересечет его поверхность по образующим – двум прямым. Вторая плоскость β – фронтально-проецирующая, линия пересечения – часть эллипса, ограниченная прямой принадлежащей линии пересечения плоскостей α и β – CN (рис. 275).
Отметим фронтальные проекции характерных точек для построения выреза – А 2, В 2, С 2, M 2, N 2 (рис. 275).
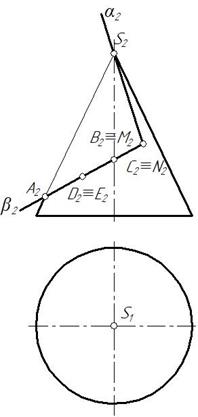
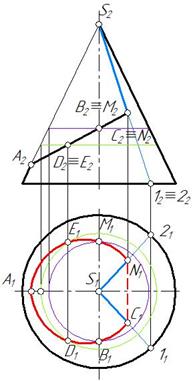
Рис. 275 Рис. 276
Точки D и Е выбираем произвольно для построения эллипса, так как линия среза от А до С N представляет собой часть эллипса.
Находим горизонтальные проекции точек А, В, С, D , Е, N. Точки находятся на поверхности конуса, а значит, они лежат линиях, принадлежащих поверхности конуса. Горизонтальные проекции точек М и В, D и E находим на окружностях, принадлежащих поверхности конуса. Точки С и N – на образующих S 1 и S 2.
Соединяем полученные горизонтальные проекции. S 1 С 1 и S 1 N 1 – прямые C 1, B 1, D 1, A 1, E 1, M 1, N 1 – кривая линия-часть эллипса (рис. 276).
Строим профильную проекцию конуса и профильные проекции точек. Соединяем их (рис. 277). Очерковая образующая удалена отМ3 до S3.
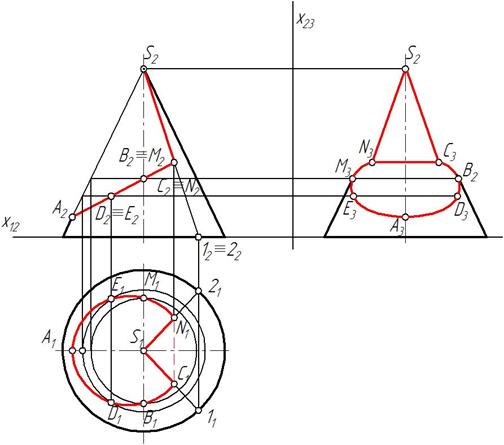
Рис. 277
Пример 2. Построить горизонтальную проекцию выреза на наклонной пирамиде (рис. 278).
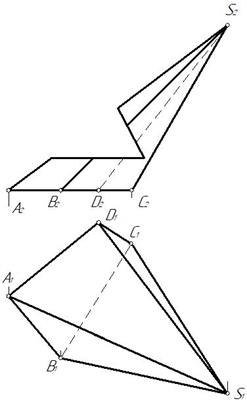
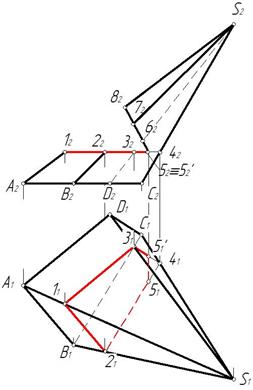
Рис. 278 Рис. 279
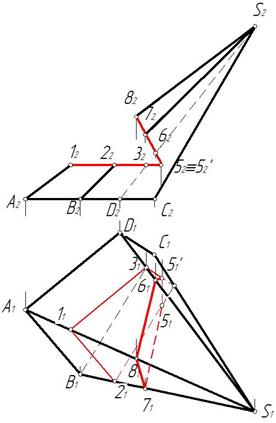
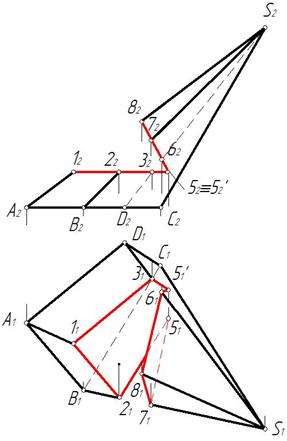
Рис. 280 Рис. 281
Поэтапное решение показано на рис. 279–281.
Пример 3. Построить горизонтальную проекцию выреза на цилиндре (рис. 282).
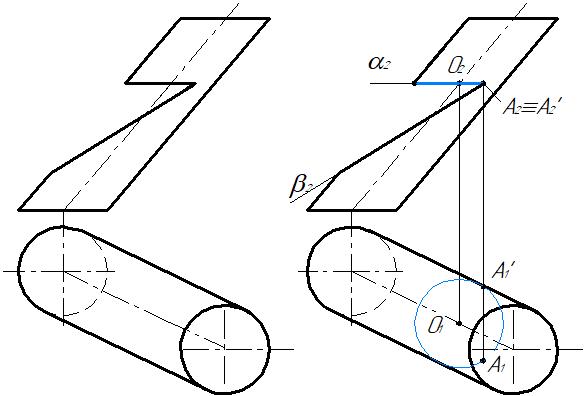
Рис. 282 Рис. 283
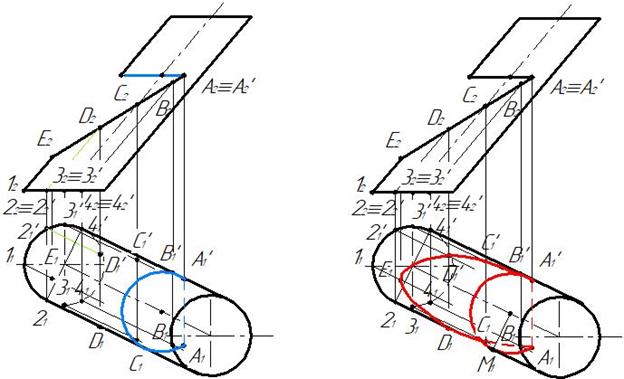
Рис. 284 Рис. 285
Список литературы
1. Гордон В. О. Курс начертательной геометрии / В. О. Гордон, М. А. Семенцов-Огиевский. – М. : Наука, 2000. – 272 с.
2. Крылов Н. Н. Начертательная геометрия / Н. Н. Крылов. – М. : Высшая школа, 2007. – 224 с.
3. Локтев О. В. Краткий курс начертательной геометрии / О. В. Локтев – М. : Высшая школа, 2001. – 130 с.
4. Фролов С. А. Начертательная геометрия / С. А. Фролов – М. : Машиностроение, 1983. – 240 с.
Приложение
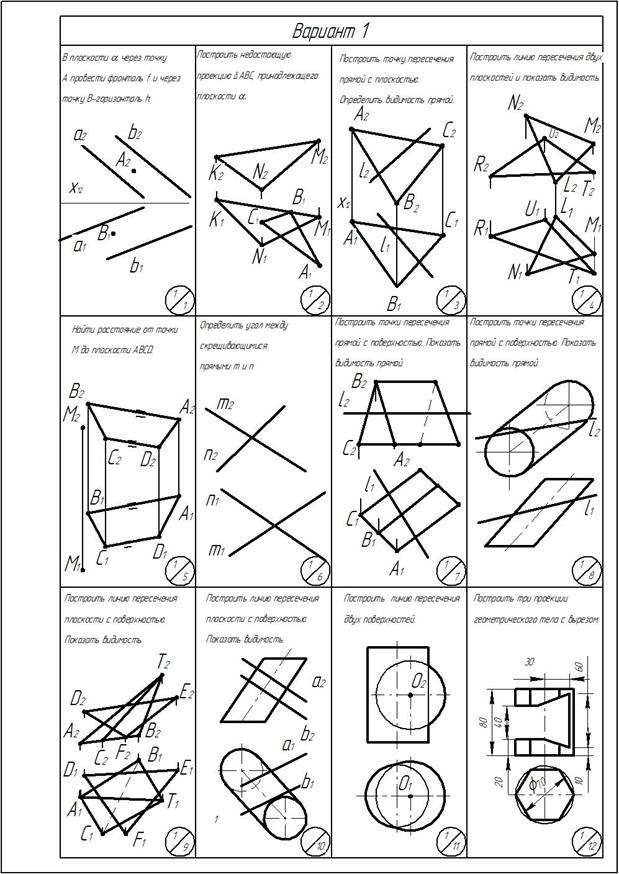
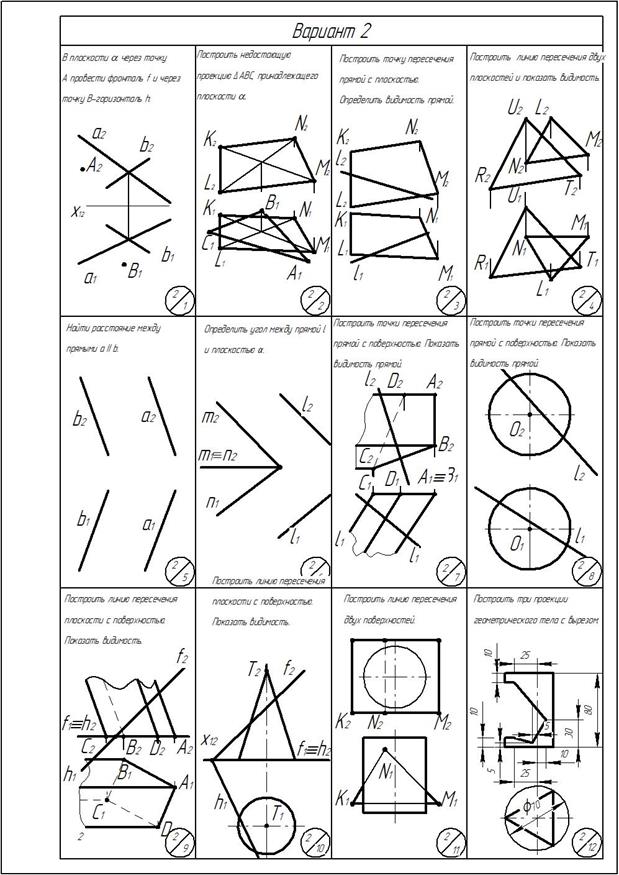
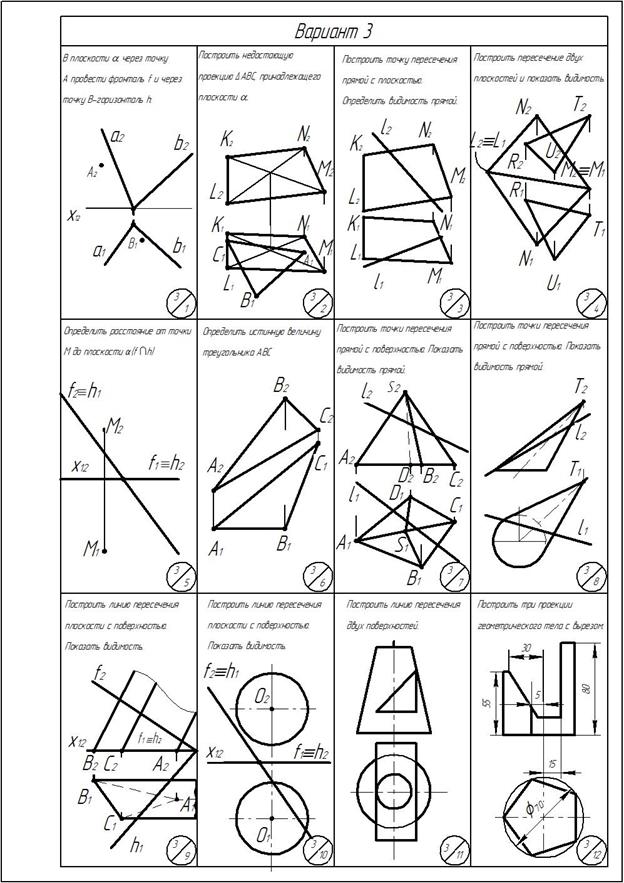
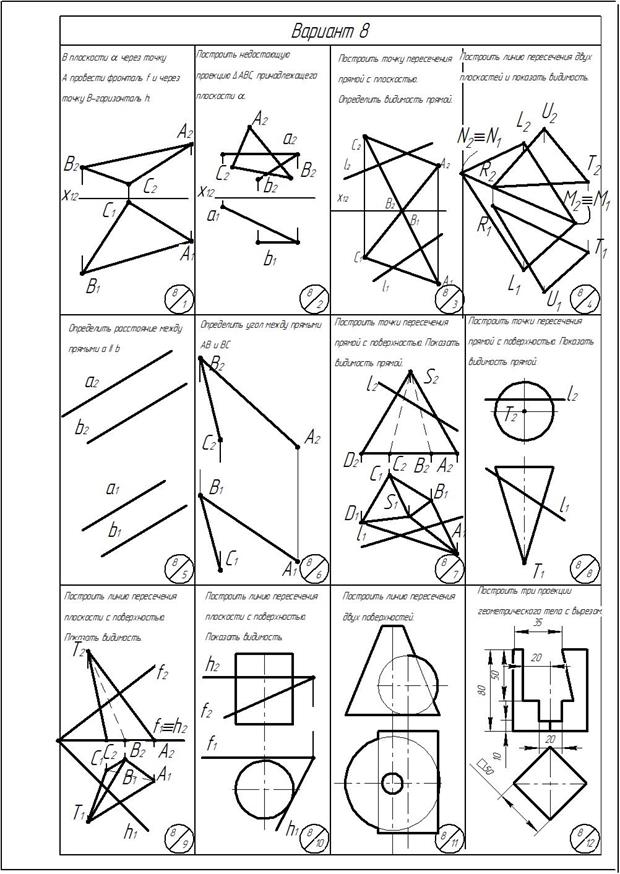
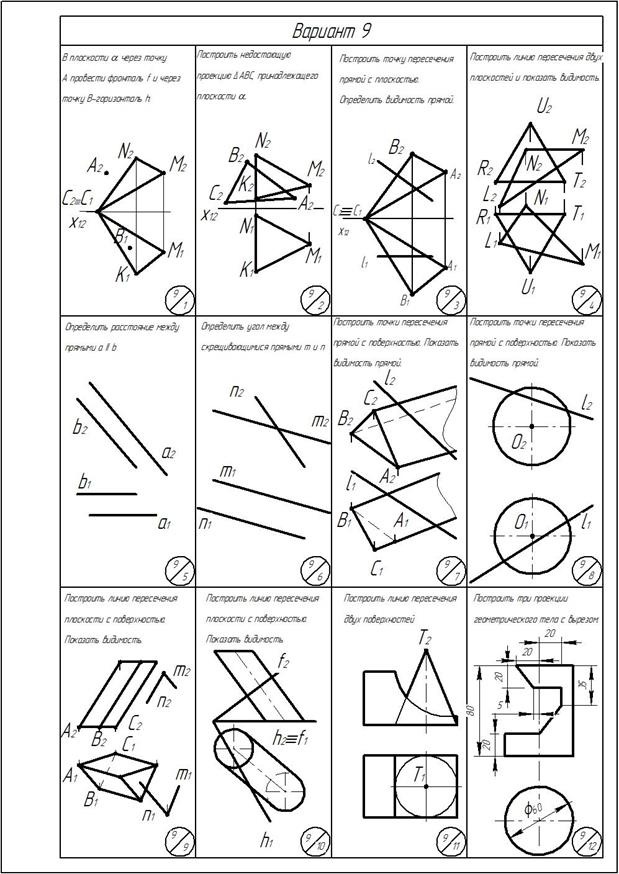
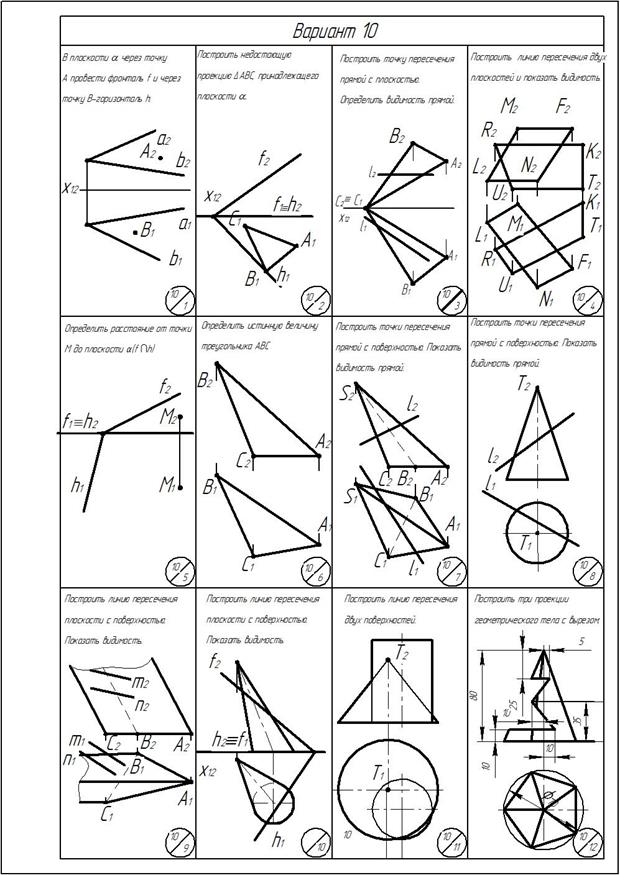
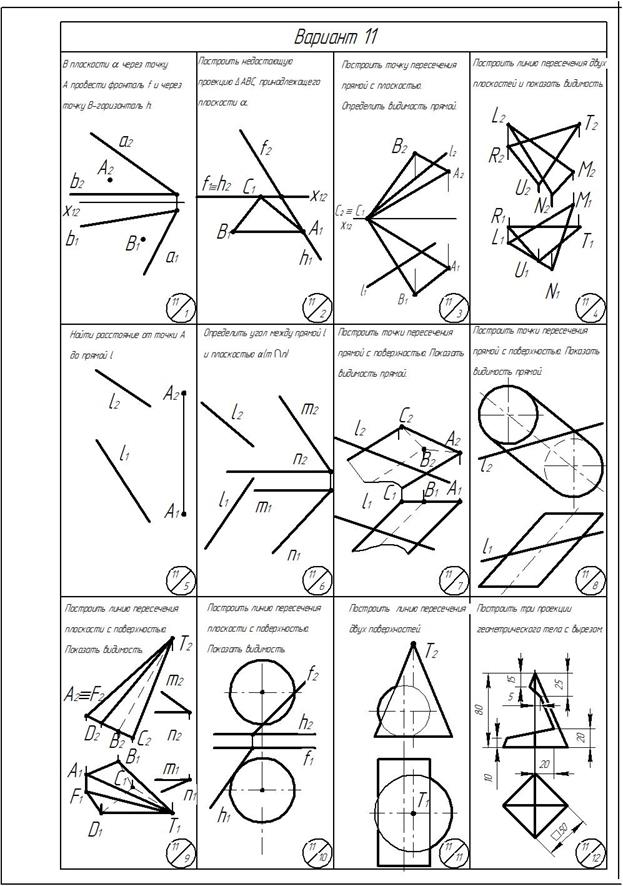
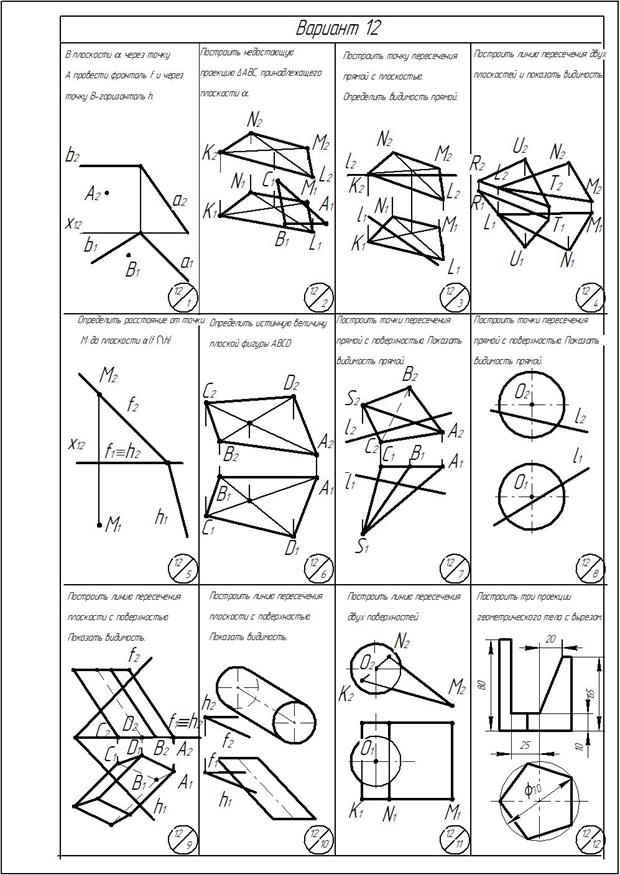
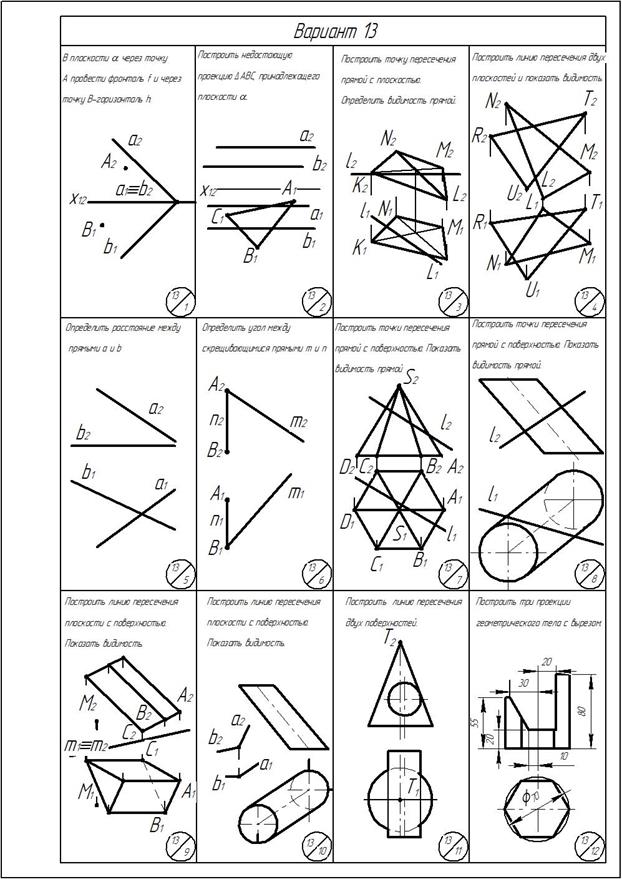
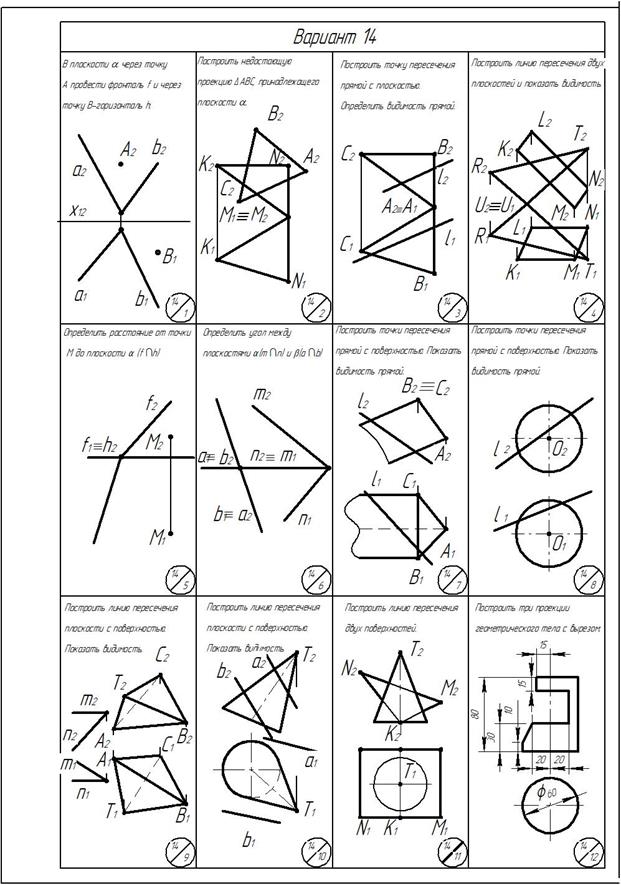
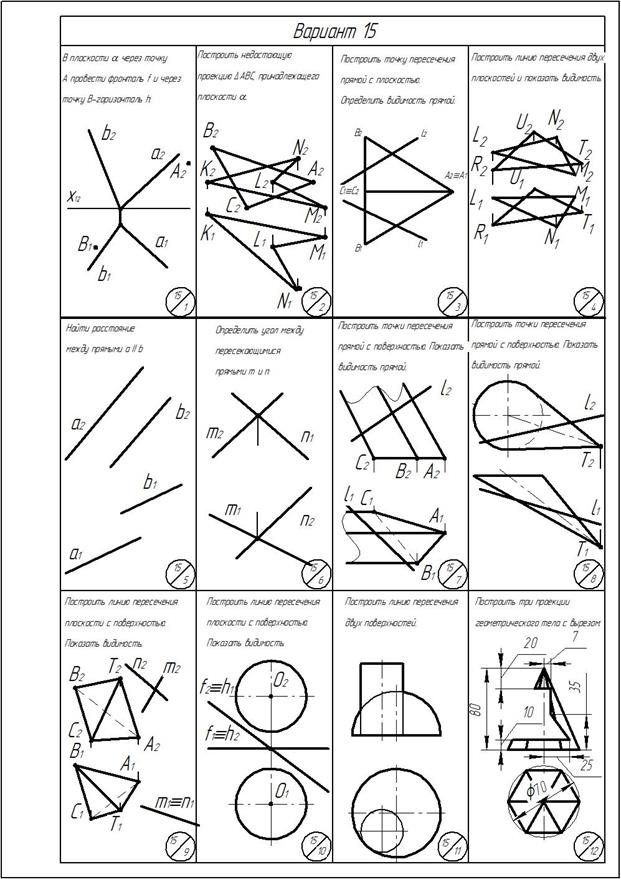
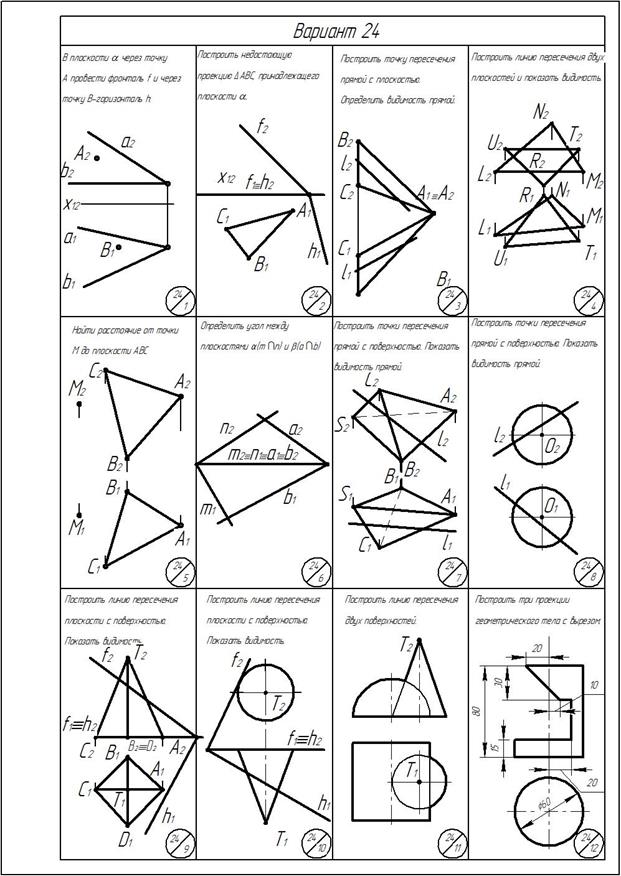
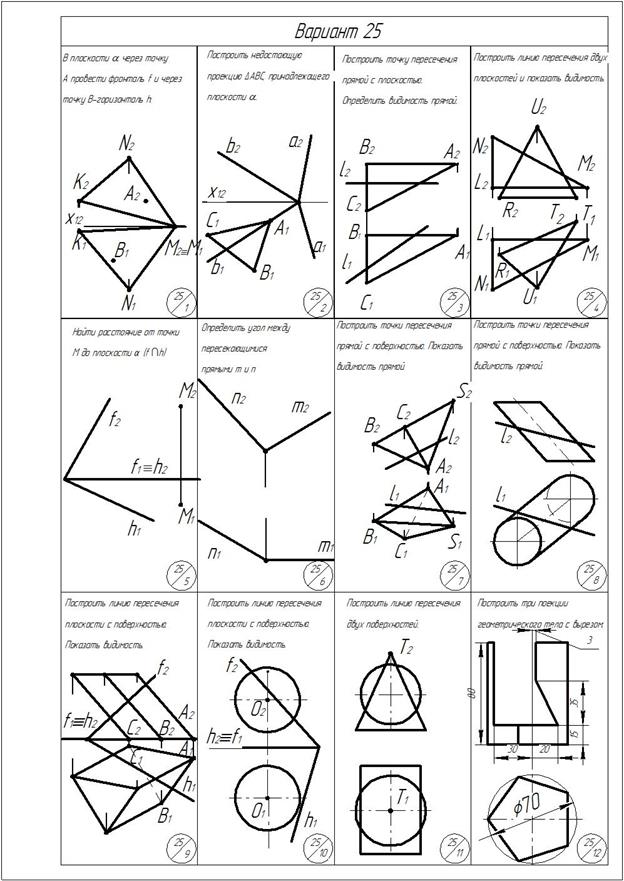
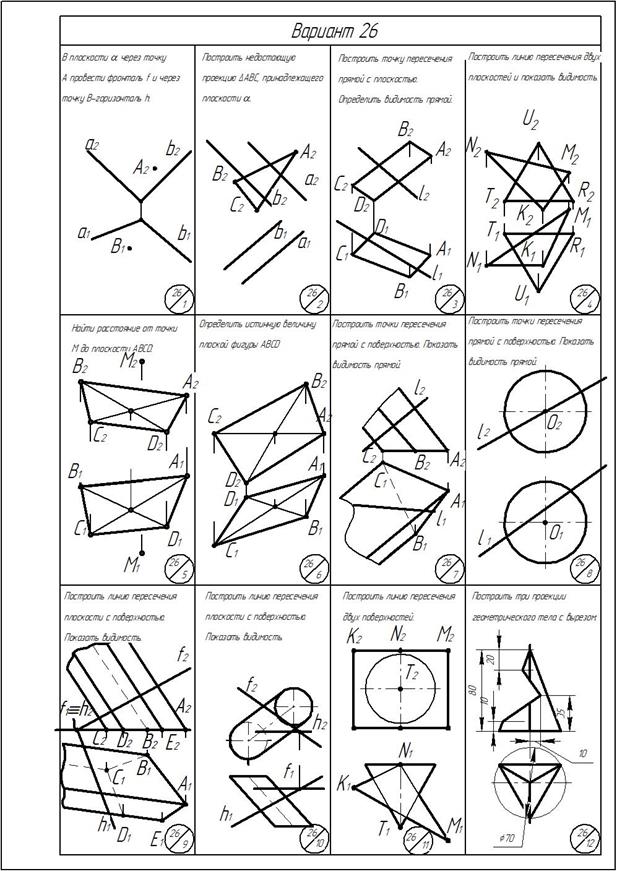
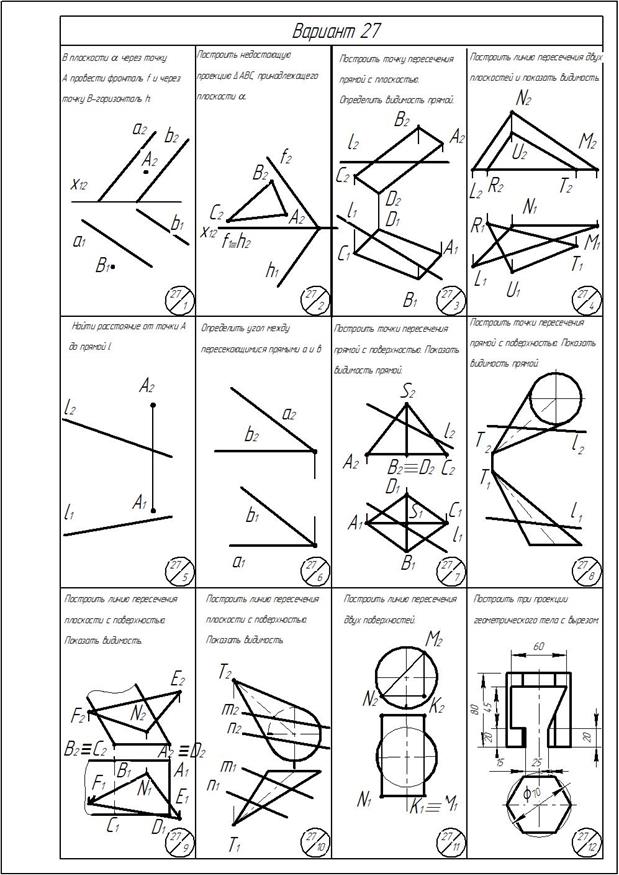
ОГЛАВЛЕНИЕ
Учебное издание
Леонова Ольга Николаевна,
Разумнова Елена Александровна
НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ.
Решение типовых задач
Учебное пособие
Редактор
Корректор
Компьютерная верстка
Подписано к печати .2018. Формат 60´84 1/16. Бум. офсетная.
Усл. печ. л. . Тираж 100 экз. Заказ . «С» .
Санкт-Петербургский государственный архитектурно-строительный университет.
Дата добавления: 2019-09-13; просмотров: 969; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
