Параллельность прямой и плоскости

Прямая параллельна плоскости, если она параллельна одной из прямых, лежащих в этой плоскости (рис. 59).

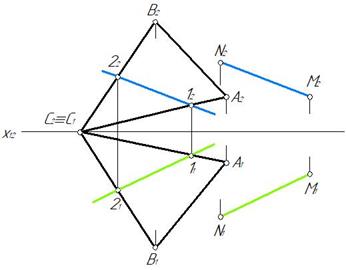
Рис. 59

 

Прямая М N параллельна плоскости α(ΔАВС), так как она параллельна прямой 1-2, принадлежащей плоскости ΔАВС. У параллельных прямых М N и 1-2 параллельны одноименные проекции.

Прямая параллельна плоскости частного положения, если одна из проекций проведенной прямой параллельна одноименной проекции плоскости, а вторая проекция прямой проводится произвольно (рис. 60).

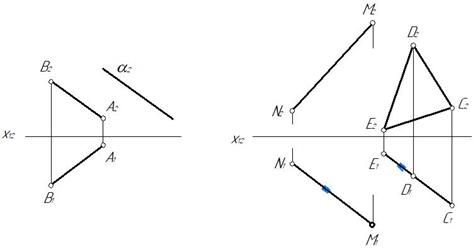
Рис. 60

 

Пример. Через точку А провести прямую d параллельную каждой из двух пересекающихся плоскостей α(f ∩ h) и β(m ∩ n) (рис. 61).

 

 

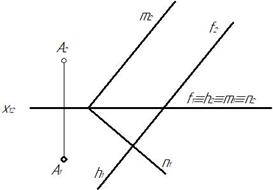
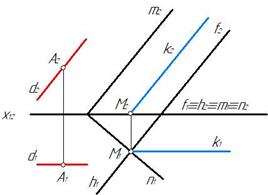
Рис. 61                                            Рис. 62

 

Две плоскости общего положения с параллельными фронталями пересекаются по фронтальной прямой, параллельной этим фронталям. Отмечаем общую точку М₁ на пересечении горизонталей h ₁ и n ₁, принадлежащих плоскости проекций П₁. По линии связи находим точку М₂ и через нее параллельно фронтальным проекциям фронталей f ₂ и m₂ строим фронталь k ₂. Горизонтальная проекция фронтали k ₁ проведена параллельно оси х₁₂. Через точку А проводим прямую d‖k (рис. 62).

 

 

Параллельность плоскостей

Если две пересекающиеся прямые одной плоскости параллельны двум пересекающимся прямым другой плоскости, то эти плоскости параллельны (рис. 63).

 

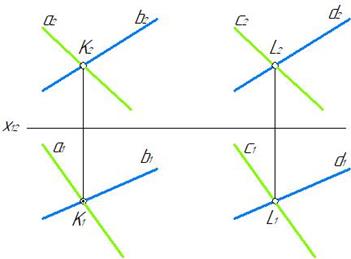
Рис. 63

 

У параллельных плоскостей параллельны горизонтали и фронтали.

Пример. Через точку N построить плоскость β параллельную плоскости α(АВ‖С D) (рис. 64).

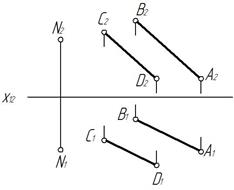
Рис. 64

 

Проводим в плоскости α(АВ‖С D) прямую k. Прямая АС пересекается с АВ. Затем через точку N проводим прямую а‖АВ и прямую b‖k. Плоскость β определена двумя пересекающимися прямыми a и b (рис. 65).

 

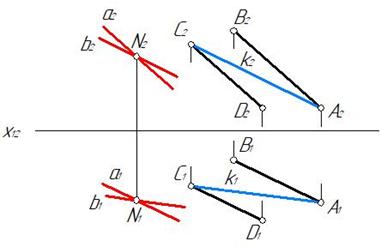
Рис. 65

 

 

Поверхности

 

Геометрическая форма отдельных предметов представляет собой сочетание простых геометрических тел, ограниченных гранными и кривыми поверхностями.

Из гранных поверхностей наиболее часто встречаются призматические и пирамидальные.

Большое распространение получили и кривые поверхности. Они входят в очертания многих деталей машиностроения и строительных конструкций. 

В начертательной геометрии поверхность рассматривается как совокупность последовательных положений линии, движущейся в пространстве по определенному закону. Линия, формирующая своим движением поверхность, называется образующей. Образующая может быть прямой или кривой линией.

Неподвижные линии, по которым движется образующая, называются направляющими.

Гранные поверхности

 

Гранные поверхности – поверхности, образованные перемещением прямолинейной образующей по ломаной линии.

 

          а)                                                                         б)

 

 

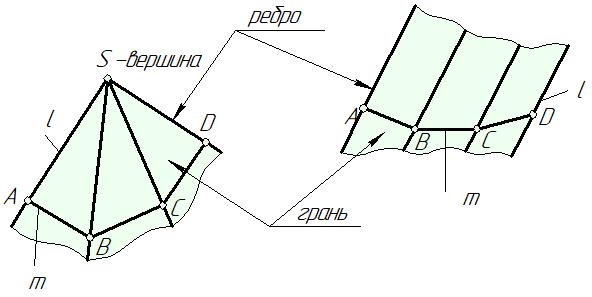
Рис. 66

 

Пирамидальная поверхность (рис. 66, а) – поверхность, образованная движением прямолинейной образующей по ломаной направляющей, при этом одна точка образующей – S неподвижна. Элементы пирамидальной поверхности: l – образующая, m – направляющая, S – вершина, ASB – грань, SA – ребро.

Призматическая поверхность (рис. 66, б) образована движением прямолинейной образующей по ломаной направляющей, при этом образующая перемещается параллельно некоторому наперед заданному направлению. Элементы призматической поверхности аналогичны элементам пирамидальной поверхности (вершина S находится в бесконечности).

Геометрическое тело, ограниченное гранной поверхностью, называется многогранником. Плоскости таких поверхностей называются гранями, общие соприкасающиеся стороны смежных граней называются ребрами.

Точка принадлежит поверхности, если она располагается на линии принадлежащей этой поверхности. Для построения точки, лежащей на грани пирамиды в плоскости этой грани проводится прямая, обычно проходящая через вершину пирамиды. На рис. 67 проведена прямая S 1 и на ней отмечена точка М.

                                

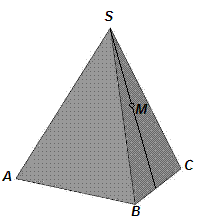
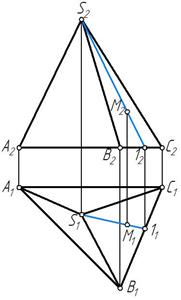
Рис. 67

       

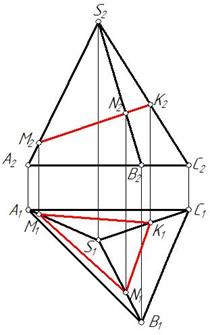
Рис. 68

 

На рис. 68 построена линия MNK, принадлежащая поверхности пирамиды.

Для построения точки, лежащей на грани наклонной призмы, в плоскости этой грани выбирается прямая, обычно параллельная ребрам призмы, и на ней строится точка. На рис. 69 в плоскости грани ВС построена прямая, параллельная ребрам и на прямой – точка М.

                 

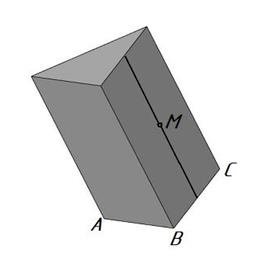
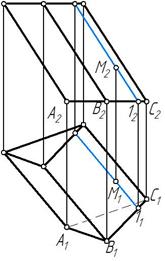
Рис. 69

 

 

Кривые поверхности

 

В зависимости от вида образующих все кривые поверхности можно подразделить на два класса:

1. Поверхность, у которой образующей является прямая линия – линейчатая поверхность.

2.  Поверхность, образующая которой кривая линия – нелинейчатая поверхность.

Из простейших линейчатых поверхностей мы рассмотрим цилиндрическую и коническую.

---

Дата добавления: 2019-09-13; просмотров: 598; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!