Пересечение прямой с плоскостью

 

Для построения точки пересечения прямой с плоскостью общего положения необходимо:

1. Через прямую провестивспомогательную плоскость (в качестве вспомогательной плоскости следует выбирать плоскости частного положения).

2. Найти линию пересечения вспомогательной плоскости с заданной плоскостью.

3. Отметить точку пересечения заданной прямой с линией пересечения плоскостей.

Пример 1. Найти точку пересечения прямой EF c плоскостью α(ΔАВС) (рис.53).

 

 

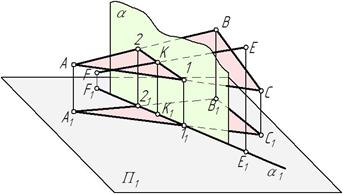
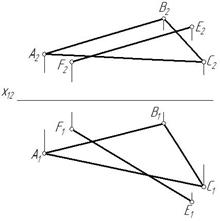
Рис. 53

 

Через прямую EF проводим вспомогательную плоскость, в качестве которой воспользуемся горизонтально-проецирующей плоскостью α. Если α⊥П₁, то на плоскость проекций П₁ плоскость α проецируется в прямую α₁, совпадающую с E₁F _1.

Строим прямую пересечения 1-2 проецирующей плоскости α с плоскостью ΔАВС. Прямая 1-2 и заданная прямая EF лежат в одной плоскости α и пересекаются в точке K. Построение на эпюре показано на рис. 54.

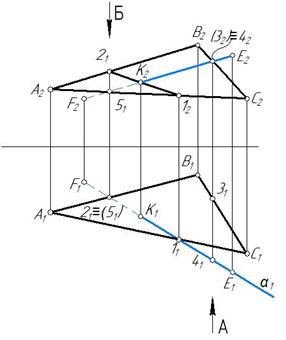
Рис. 54

 

Определяем видимость прямой EF. Для определения видимости на П₂ отметим точки 3 и 4, у которых совпадают фронтальные проекции. Направление взгляда А указано стрелкой. Горизонтальная проекция 4₁ находится ближе к наблюдателю, чем 3₁. Точка 4 принадлежит EF. Следовательно, E₂K₂ видима, в точке K₂ видимость прямой меняется. За очертаниями треугольника прямая всегда видима.

Для определения видимости на П₁ отметим точки 2 и 5, у которых совпадают горизонтальные проекции. Направление взгляда Б на П₁ показано стрелкой. Точка 2₂ находится выше, чем точка 5₂. Точка 2 принадлежит прямой АВ треугольника ΔАВС. Следовательно, прямая ЕF находится под плоскостью ΔАВС и на участке 2₁ K₁ невидима до точки K₁. В точкеK₁ видимость прямой меняется.

Пример 2. Найти точку пересечения прямой l с плоскостью α(Δ АВС). Определить видимость прямой l (рис. 55).

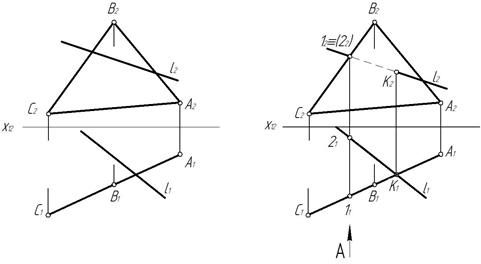
Рис. 55                                                     Рис. 56

 

Плоскость α(ΔАВС) является горизонтально-проецирующей. На пересечении горизонтальной проекции l ₁ прямой l и горизонтальной проекции плоскости А₁В₁С₁ отмечаем горизонтальную проекцию K₁ точки K. Фронтальную проекцию K₂ точки K отмечаем на фронтальной проекции прямой l. Для определения видимости рассмотрена видимость точек 1 и 2 относительно плоскости проекций П₂. Так как горизонтальная проекция 1₁ точки 1 находится перед горизонтальной проекцией 2₁ точки 2, точка 1 видима относительно фронтальной плоскости проекций. Точка 1 принадлежит плоскости треугольника, значит, справа прямая l закрыта треугольником (не видима). В точке K₂ видимость меняется (рис. 56).

Пример 3. Найти точку пересечения прямой l плоскостью α(f∩h) (рис. 57).

 

                    

 

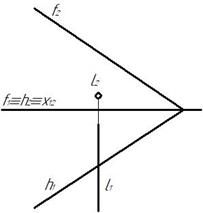
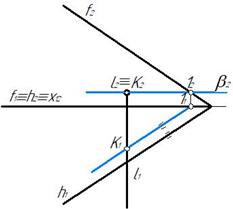
Рис. 57                                                                               Рис. 58

 

Плоскость α является плоскостью общего положения, прямая l^П₂. Для решения задачи воспользуемся общим алгоритмом нахождения точки пересечения прямой с плоскостью общего положения. Для этого через прямую l проводим вспомогательную плоскость частного положения β‖П₁. Затем строим линию пересечения плоскости α и β – горизонталь параллельную h и отмечаем точку K₁ (рис. 58). Фронтальная проекция K₂ совпадает с фронтальной проекцией прямой l ₂. Видимость прямой l отмечать не будем.

---

Дата добавления: 2019-09-13; просмотров: 730; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!