Точка на прямой. Деление отрезка на части
Если точка лежит на прямой, то проекции этой точки лежат на одноименных проекциях прямой (рис. 16)
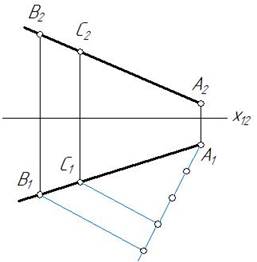
Рис. 16
Если точка делит проекцию отрезка прямой в определенном отношении, то проекции этой точки делят проекции отрезка в том же отношении. На рис.16 показано деление отрезка АВ в отношении АС:СВ=3:1. Деление отрезка выполняется на основе теоремы Фалеса. Через А1 проводят прямую под произвольным углом. На вспомогательной прямой откладывают 4 отрезка (всего 4 части). Конец последнего отрезка соединяют с точкой В1 и параллельно этой прямой проводят прямую, отсчитав одну часть. Точка С делит отрезок в отношении 3:1.
Пример 1. Построить фронтальную проекцию отрезка АВ параллельного горизонтальной плоскости проекций П1 и отстоящего от нее на 30 мм. Найти на АВ точку С, удаленную от плоскости проекций П2 на 20 мм (рис. 17).

Рис. 17
Фронтальная проекция горизонтальной прямой всегда параллельна оси х12. Откладываем от оси х12 30 мм вверх и параллельно оси строим А2В2.

Рис. 18
Точку С строим так, чтобы фронтальная проекция С2 располагалась на фронтальной проекции А2В2 прямой АВ, а горизонтальная С1 на горизонтальной проекции А1В1. Откладываем 20 мм вниз от оси х12 и отмечаем С1. Затем проводим линию проекционной связи и отмечаем С2 (рис. 18).
Пример 2. Построить через точку А отрезок длиной 20 мм.
1) АВ^ П1; 2) АС^П3 (рис. 19).

Рис. 19
Строим отрезок АВ^П1. Фронтальная проекция горизонтально-проецирующего отрезка прямой перпендикулярна оси х12 и отрезок проецируется на плоскость проекций П2 в натуральную величину.
|
|
|
Таким образом, откладываем 20 мм на вертикальной прямой и получим фронтальную проекцию А2В2 отрезка АВ. Горизонтальная проекция отрезка есть точка.
Строим отрезок АС^П3. Фронтальная и горизонтальная проекция отрезка профильно-проецирующей прямой параллельна оси х12 и на плоскости П1 и П2 отрезок проецируется в натуральную величину. Откладываем отрезок А1С1 и А2С2 длиной 20 мм (рис. 20).
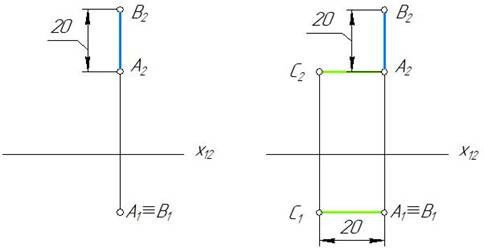
Рис. 20
Пример 3. Через точку А провести отрезок АВ длиной 30 мм, параллельный фронтальной плоскости проекций П2 и наклоненный к плоскости проекций П1 под углом 45° (рис. 21).

Рис. 21
Отрезок фронтальной прямой с проецируется в натуральную величину на плоскость проекций П2. Строим фронтальную проекцию отрезка А2В2 длиной 30 мм под углом 45° к оси х12. Горизонтальная проекция фронтальной прямой всегда параллельна оси х12 (рис. 21).
Взаимное положение прямых
Пересекающиеся прямые
Пересекающиеся прямые имеют общую точку. Проекции этой точки должны принадлежать одноименным проекциям обеих прямых. Из этого следует, что точки пересечения одноименных проекций пересекающихся прямых лежат на одной линии связи. На рис. 22 изображены пересекающиеся в точке D прямые m и n.
|
|
|

Рис. 22
Параллельные прямы е
У параллельных прямых параллельны одноименные проекции. На рис. 23 изображены параллельные прямые m и n.
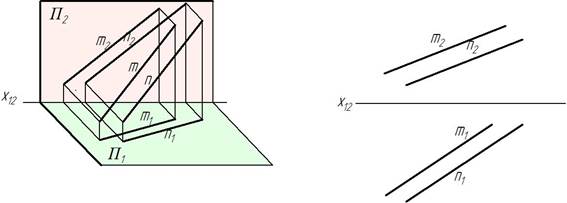
Рис. 23
Скрещивающиеся прямые
Скрещивающиеся прямые не имеют общей точки. Следовательно, точка пересечения одноименных проекций таких прямых (например, m и n, рис. 24) не лежит на одной линии связи, так как каждая из них является изображением двух разных точек (точки 1, 2 и 3, 4).

Рис. 24
Пример. Определить взаимное положение прямых. Определить видимость точек, расположенных на скрещивающихся прямых (рис. 25).

Рис. 25
Прямые m и n находятся в одной плоскости (совпадают их горизонтальные проекции) и имеют общую точку K. Прямые m и n пересекающиеся.
Прямые a и b скрещиваются и не имеют общей точки. В месте пересечения фронтальных проекций отмечаем две точка А и В. Фронтальная проекция точки В не видима относительно плоскости проекций П2, так как горизонтальная проекция А1 находится ближе к наблюдателю при взгляде по направлению А. Невидимую проекцию В2 закрываем в скобки (рис. 26).
|
|
|

Рис. 26
Прямые c и d также скрещиваются. Точку пересечения фронтальных и горизонтальных проекций нельзя соединить одним перпендикуляром к оси х12. Скрещивающиеся прямые не имеют общей точки. Поэтому в месте пересечения фронтальных и горизонтальных проекций прямых с и d отмечаем две точки и определяем их видимость относительно плоскостей проекций. Невидимые точки закрыты в скобки (рис. 26).
Дата добавления: 2019-09-13; просмотров: 590; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
