Пересечение поверхности плоскостью

Плоскость пересекает поверхность по плоской линии, вид которой зависит от формы поверхности. Линия пересечения плоскости с поверхностью многогранника – ломаная линия, с кривой поверхностью – обычно кривая линия.

 

Конические сечения

 

При пересечении конуса плоскостью получаются следующие плоские кривые:

1) окружность (рис. 82)или эллипс (рис. 83) – если плоскость пресекает все образующие;

        

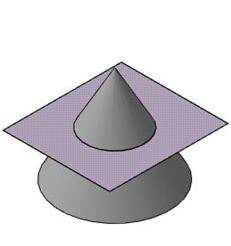
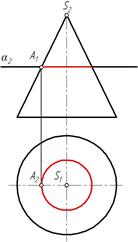
Рис. 82

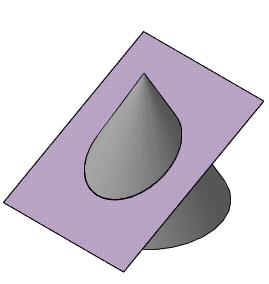
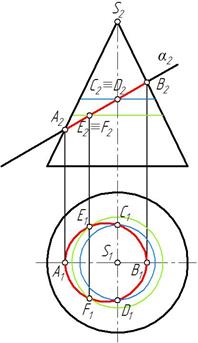
Рис. 83

 

2) парабола (рис. 84) – если плоскость параллельна одной образующей;

    

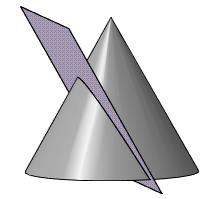
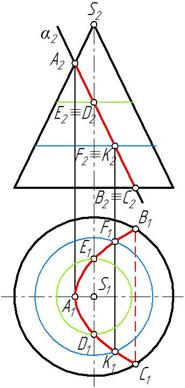
Рис. 84

 

3) гипербола (рис. 85) – если плоскость параллельна двум образующим;

 

   

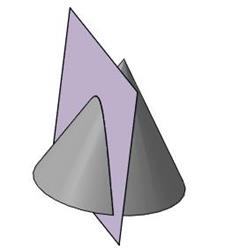
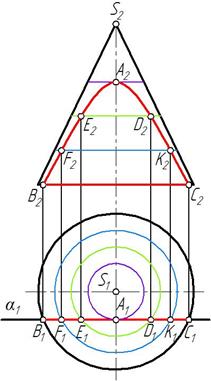
Рис. 85

 

4) две образующие (рис. 86) – если плоскость проходит через вершину конуса.

                

 

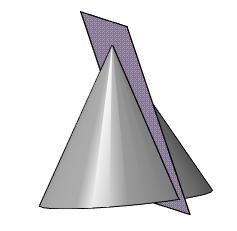
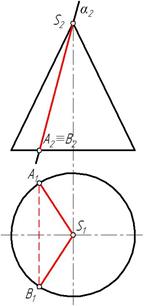
Рис. 86

 

Пример. Построить линию пересечения наклонного конуса с плоскостью частного положения α(α₂) (рис. 87).

 

 

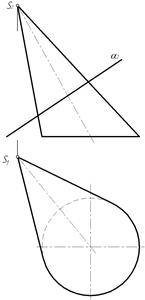
Рис. 87

 

Линией пересечения фронтально-проецирующей плоскости с поверхностью наклонного конуса будет эллипс, точки которого расположены на образующих конуса. Поскольку плоскость фронтально-проецирующая, фронтальные проекции точек пересечения располагаются на фронтальной проекции плоскости α₂. Точки А и В отмечаем на фронтальных проекциях очерковых образующих конуса. Отмечаем характерные точки С и D линии пересечения, находящиеся на горизонтальных проекциях образующих S 3 и S 4, в которых будет меняться видимость эллипса (рис. 88). Точка М выбрана произвольно.Построены ее проекции (рис. 89).

               

 

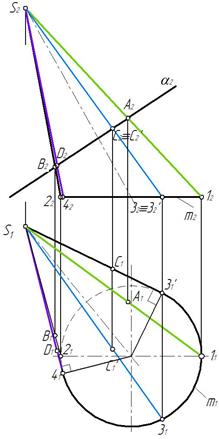
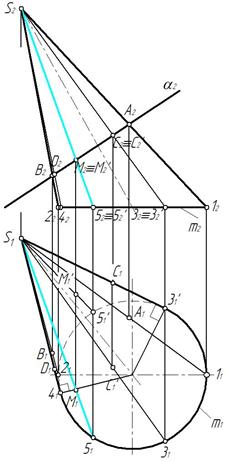
Рис. 88                                               Рис. 89

 

Построив горизонтальные проекции точек на соответствующих горизонтальных проекциях образующих, соединяем их с учетом видимости (рис. 90). Видимость меняется в точках С₁ и D ₁ на очерковых образующих конуса.

 

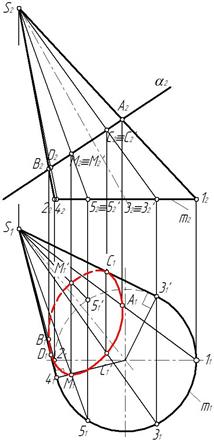
Рис. 90

 

Пересечение сферы плоскостью

Линия пересечения сферы с плоскостью представляет собой окружность.

     

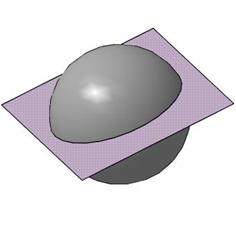
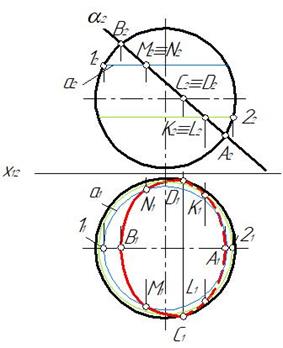
Рис. 91

 

Если окружность находится в наклонной плоскости, то она проецируется в виде эллипса. На рис. 91 фронтальная проекция линии пересечения совпадает с фронтальной проекцией плоскости α, а горизонтальная – эллипс. Построим его по точкам. Отмечаем характерные точки, находящиеся на экваторе и главном меридиане – А, В, С, D. Для нахождения других точек, например М и N, проводим по поверхности сферы линию а, горизонтальная проекция которой является окружностью и отмечаем на ней проекции этих точек. Аналогично строим точки K и L. Горизонтальные проекции полученных точек соединяем плавной линией с учетом видимости. Точки, находящиеся ниже экватора – А₁, K ₁, L ₁ не видимы относительно плоскости проекций П₁. В точках C₁ и D ₁ на экваторе меняется видимость эллипса.

Пример. Построить линию пересечения сферы плоскостью ψ(a∩b) (рис. 92).

 

 

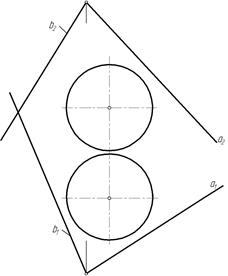
Рис. 92

 

Заданная плоскость является плоскостью общего положения.

Плоскость пересекает сферу по окружности,проекции которой в общем случае на ортогональном чертеже изобразятся эллипсами. Точки пересечения плоскости со сферой можно рассматривать как точки пересечения окружностей сферы с плоскостью. Для построенияя линии пересечения плоскости со сферой определим характерные точки.проекции которых лежат на очерках сферы.

Для нахождения точек А и В на экваторе сферы через экватор проводим вспомогательную горизонтальную плоскость α, которая пересечет заданную плоскость ψ(а∩b) по горизонтали 1-2. Взаимное пересечение горизонтальных проекций экватора и горизонтали 1-2 определяет горизонтальные проекции А₁ и В₁ точек А и В. Фронталные проекции этих точек отмечены в проекционной связи (рис. 93).

Для нахождения точек С и D на главном меридиане через него проводим вспомогательную фронтальную плоскость β, которая пересечет заданную плоскость ψ(а∩b) по фронтали 3-4. Взаимное пересечение фронтальных проекций главного меридиана и фронтали 3-4 определяет фронтальные проекции С₂ и D₂ точек C и D. Горизонтальные проекции этих точек отмечены в проекционной связи (рис. 94).

Для нахождения других точек проводится вспомогательная горизонтальная плоскость, например, γ. Плоскость γ пересекает поверхность сферы по окружности, а заданную плоскость ψ(а∩b) по горизонтали 5-6. Взаимное пересечение горизонтальных проекций этих линий определяет горизонтальные проекции точек M и N (рис. 95). Аналогично строим точки K и L.

 

 

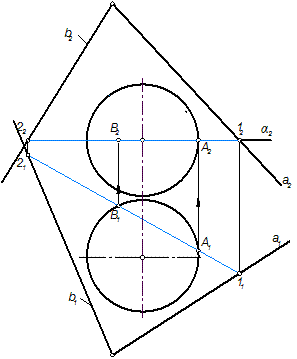
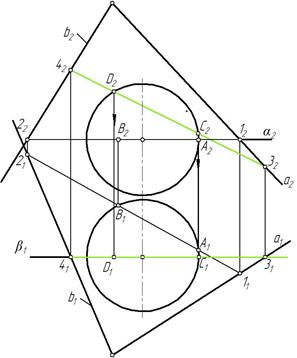
Рис. 93                                                   Рис. 94

 

Полученные точки А, В, С, D, M, N, K, L соединяем плавной кривой с учетом видимости. Горизонтальные проекции точек А и В отделяют видимую на П₁ часть кривой от невидимой. Фронтальные проекции точек С и D отделяют видимую на П₂ часть кривой от невидимой (рис. 96).

 

                   

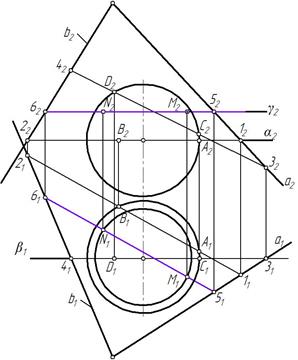
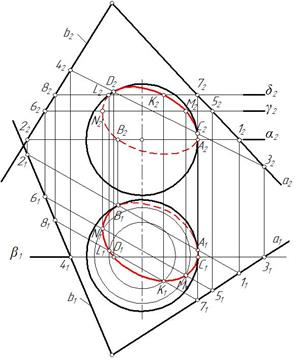
Рис. 95                                                                         Рис. 96

---

Дата добавления: 2019-09-13; просмотров: 508; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!