Построение линии пересечения поверхностей способом вспомогательных

Концентрических сфер

Рис. 134

Способ вспомогательных сфер применяется для построения линии пересечения двух поверхностей вращения при условии, что оси поверхностей пересекаются и параллельны одной из плоскостей проекций. Этот способ основан на следующем. Известно, что сфера пересекается по окружности с любой поверхностью вращения, если ось поверхности вращения через центр сферы. На рис. 134 изображена одна фронтальная проекция, причем общая ось поверхностей расположена параллельно фронтальной плоскости. Поэтому окружности, получаемые при пересечении одной поверхности другой, проецируются на фронтальную плоскость в виде прямолинейных отрезков (пересечение сферы с цилиндром, усеченного конуса со сферой и двух сфер).

Пример 1. Построить линию пересечения двух цилиндров (рис. 135)

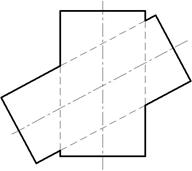
Рис. 135

Оси цилиндров пересекаются в точке О и параллельны плоскости проекций П₂. Для построения линии пересечения можно применить метод вспомогательных концентрических сфер, которые пересекут цилиндры по окружностям, а последние спроецируются на плоскость П₂ в виде отрезков прямых.

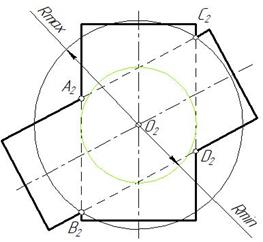
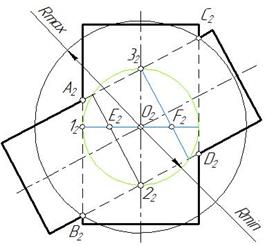
Рис. 136 Рис. 137

Отмечаем характерные точки линии пересечения А, В, С, D фронтальные проекции которых находятся на пересечении очерковых образующих цилиндров. На рис. 136 показана вспомогательная сфера с наибольшим радиусом. Радиус R_max равен расстоянию наиболее удаленной точки пересечения очерковых образующих заданных поверхностей от точки пересечения их осей. Радиус наименьшей сферы R_min равен радиусу большей сферы, которую можно вписать в заданные цилиндры.

Сфера с минимальным радиусом пересечет прямой цилиндр по окружности, которая проецируется в виде отрезка, проходящего через точку 1₂. Наклонный цилиндр сфера с минимальным радиусом пересечет по окружностям, которые проецируются в виде отрезков прямых ,проходящих через точки 2₂ и 3₂. На персечении отрезков отмечаем точки Е₂ и F ₂ (рис. 137).

Затем проведем сферу произвольного радиуса. Эта сфера пересекает прямой цилиндр в точке 4₂ по окружности, которая проецируется в виде отрезка. Наклонный цилиндр эта сфера пересекает в точке 5₂ по окружности, которая также проецируется в виде отрезка. На пересечении этих отрезков отмечена точка N ₂. Аналогично можно получить точку М₂ (рис. 138).

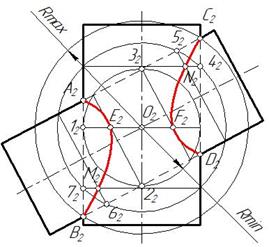
Рис. 138 Рис. 139

Полученные точки соединяем плавной линией.. Линия пересечения распадается на две части (рис. 139).

Пример 2. Построить линию пересечения двух цилиндров (рис. 140).

Рис. 140

В данном примере в заданные цилиндры можно вписать сферу. Поэтому она решается по теореме Монжа: если две поверхности второго порядка описаны около третьей или вписаны в нее, то линия пересечения распадается на две плоские кривые второго порядка (рис. 140).

Линией пересечения являются два эллипса.

Пример 3. Построить линию пересечения двух цилиндров (рис. 141).

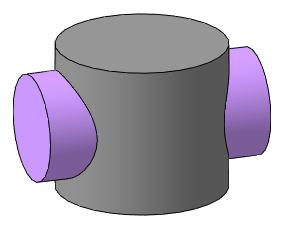
Рис. 141

Оси цилиндров пересекаются в точке O и параллельны плоскости проекций П₂. Для решения задачи применим метод концентрических сфер. На рис. 142 показано определение максимального и минимального радиуса вспомогательных сфер. Так же отмечены характерные точки А₂, В₂, С₂, D ₂ на пересечении фронтальных очерков цилиндров. Сфера минимального радиуса пресекает заданные цилиндры по окружностям, проходящим через точки 1₂ и 2₂. Эти окружности проецируются в виде отрезков прямых и в пересечении этих отрезков отмечаем точки Е₂ и F ₂. Аналогично определяем точки М₂ и N ₂_.

Рис. 142 Рис. 143

Для определения промежуточных точек проводим сферу произвольного радиуса, но меньшую чем максимального радиуса. Проекции окружностей, по которым сфера произвольного радиуса пересечет оба цилиндра – отрезки прямых. Попарно пересекаясь, эти прямые определяют фронтальные проекции точек искомой линии. Полученные точки соединяем плавной кривой (рис. 143).

Пример 4. Построить линию пересечения конуса и цилиндра (рис. 144).

Рис. 144

В заданные поверхности можно вписать сферу, следовательно задача решается по теореме Монжа. Линия пересечения конуса и сферы распадается на две плоские кривые m и n, которые являются эллипсами (рис. 145). На фронтальной проекции эти эллипсы изображаются отрезками А₂ D ₂ и В₂С₂. Для построения горизонтальных проекций эллипсов необходимо найти точки на поверхности конуса и соединить их с учетом видимости (рис. 146).

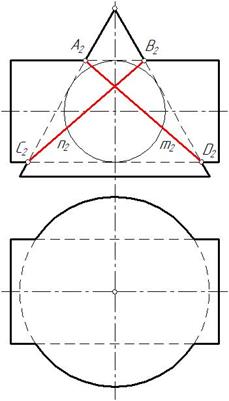
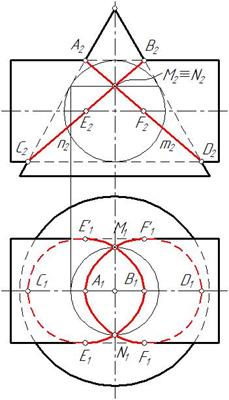
Рис. 145 Рис. 146

Дата добавления: 2019-09-13; просмотров: 738; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 8 9 10 11 12 131415 16 17 Следующая ⇒

Мы поможем в написании ваших работ!