Пересечение цилиндра плоскостью

Линией пересечения поверхности цилиндра плоскостью может быть окружность, две образующие, эллипс.

Пример 1. Построить линию пересечения цилиндра плоскостью α(f∩h) (рис. 97).

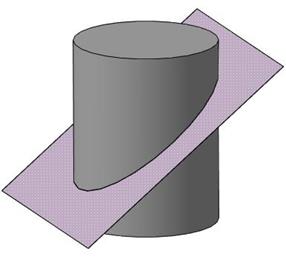
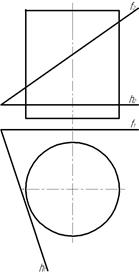
Рис. 97

Линией пересечения прямой круговой цилиндрической поверхности плоскостью общего положения является эллипс. Данная цилиндрическая поверхность является горизонтально-проецирующей, так как ее образующие перпендикулярны горизонтальной плоскости проекций. Следовательно, линия пересечения, как принадлежащая такой поверхности, на горизонтальную плоскость проекций проецируется в виде очерка этой поверхности, т. е. в виде окружности. На фронтальную плоскость проекций линия пересечения проецируется в виде эллипса.

Точки эллипса построены по принадлежности их плоскости α(h∩f) при помощи фронталей. Фронтальные проекции точек С и K отделяют видимую часть эллипса от невидимой части (рис. 98).

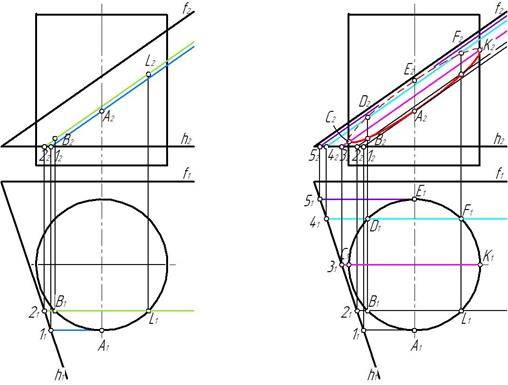
Рис. 98

Пример 2. Построить линию пересечения наклонного цилиндра с фронтально-проецирующей плоскостью ψ( ψ₂) (рис. 99).

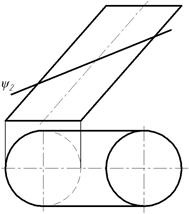
Рис. 99

Линией пересечения плоскости ψ с поверхностью цилиндра будет эллипс. Фронтальная проекция эллипса совпадает с фронтальной проекцией плоскости ψ₂.

Горизонтальную проекцию эллипса построим по точкам. Определяем проекции характерных точек, находящихся на очерковых образующих.

Это проекции точек А', В', С', D' (рис. 100). Затем отмечаем две произвольные точки 1' и 2', принадлежащие образующим цилиндра 1 и 2 и плоскости ψ, а также точки 3 и 4. Полученные точки соединяем плавной кривой с учетом видимости. Точки 1'₁, 2'₁, В'₁, С'₁, D '₁ принадлежат видимым образующим, следовательно они видимы. На очерковых образующих в точках С'₁ и D '₁ меняется видимость, т. е. эллипс становится невидимым (рис. 101).

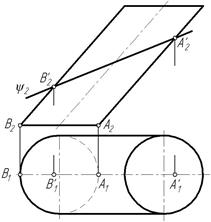
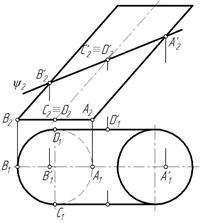
Рис. 100

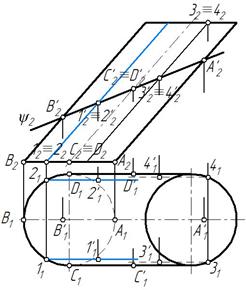
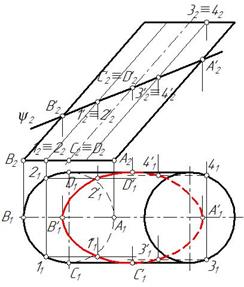
Рис. 101

Пересечение пирамиды плоскостью

Линия пересечения поверхности многогранника плоскостью будет плоская ломаная линия,состоящая из звеньев прямых.

Пример 1. Построить линию пересечения пирамиды фронтально-проецирующей плоскостью α(α₂) (рис. 102).

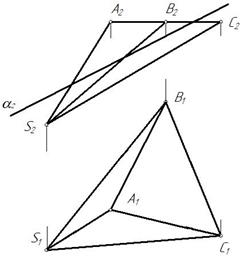
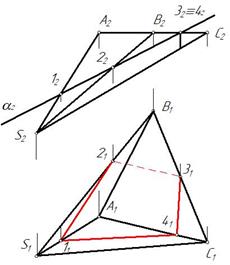
Рис. 102 Рис. 103

Фронтально-проецирующая плоскость пересекает основание пирамиды АВС в точках 3 и 4. Ребра SА и SB плоскость пересекает в точках 1 и 2 соответственно. Строим проекции точек 1, 2,3 и 4 и соединяем их горизонтальные проекции с учетом видимости. Грань ВSС невидима относительно плоскости проекций П₁, следовательно, прямая 2₁ 3₁ невидима (рис. 103).

Пример 2. Построить линию пересечения пирамиды плоскостью α(f∩h) (рис. 104).

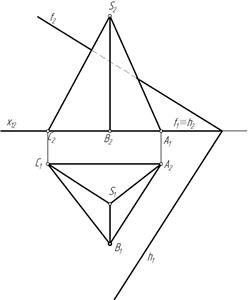
Рис. 104

Линией пересечения трехгранной пирамиды с плоскостью будет треугольник,точки которого принадлежат ребрам пирамиды. Поскольку ребро SA является профильной прямой задачу целесообразно решать при помощи дополнительного ортогонального проецирования.

Преобразуем плоскость α(h∩f) из общего положения в частное, для этого построим дополнительную ортогональную проекцию плоскости α на плоскость ей перпендикулярную. П₄^α и П₄^П₁(рис. 105). Проводим ось х₁₄^ h₁и строим дополнительную проекцию плоскости и пирамиды.

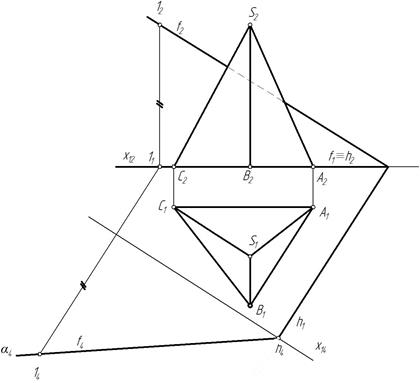
Рис. 105

На фронтали отмечаем произвольную точку 1, строим дополнительную проекцию 1₄, горизонталь спроецируется в точку. Плоскость спроецируется в прямую α₄. Строим также дополнительную ортогональную проекцию пирамиды. На пересечении с проекциями ребер пирамиды отмечаем дополнительные проекции точек М₄, N_4, K₄ (рис. 106).

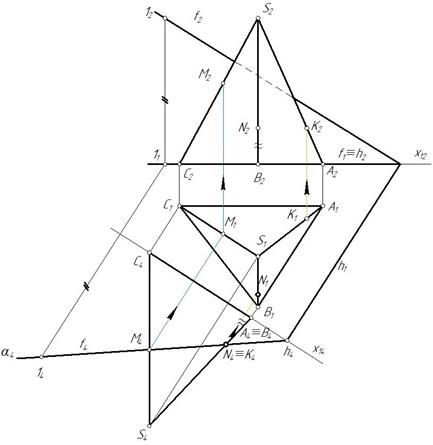
Рис. 106

Затем находим горизонтальные и фронтальные проекции этих точек и соединяем их с учетом видимости (рис. 107). Грань АSC не видима относительно плоскости проекций П₂, прямая K ₂ М₂ не видима.

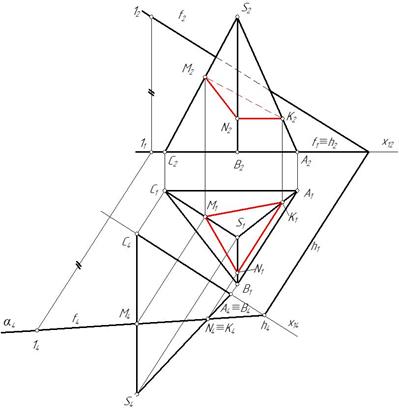
Рис. 107

Дата добавления: 2019-09-13; просмотров: 3004; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 6 7 8 9 101112 13 14 15 Следующая ⇒

Мы поможем в написании ваших работ!