Пересечение кривой поверхности с поверхностью многогранника
Грани многогранника, вобщем случае, пересекают кривую поверхность по плоским кривым линиям, пересекающимся между собой в точках, лежащих на ребрах многогранника.
Пример. Построить линию пересечения конуса и трехгранной призмы (рис. 122).
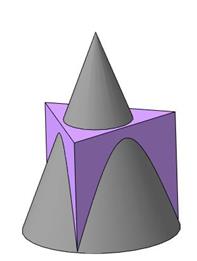

Рис. 122
Верхннее основание призмы пересекает поверхность конуса по окружности. Боковые грани призмы пересекаются с поверхностью конуса по гиперболам. Определим самые высокие точки гипербол. Для этого на горизонтальной проекции проводим окружность, касающуюся граней призмы и опускаем перпендикуляры, чтобы определить точки касания D 1 и Е1. Эта окружность на фронтальной плоскости проекций спроецируется как отрезок, параллельный основанию конуса.
Отметим характерные точки K и F, находящиеся на очерковых образующих конуса. Фронтальные проекции K2 и F 2 будут определять границы видимости линий пересечения на гранях АС и ВС (рис. 123).


Рис. 123 Рис. 124
Для нахождения промежуточных точек гипербол строим еще окружность и отмечаемм точки 11, 21, 31, 41, 51, 61. Фронтальные проекции этих точек определяем по линии связи на фронтальной проекции этой окружности. Полученные точки соединяем плвавной кривой с учетом видимости. Фронтальная проекция гиперболы на грани АВ невидима, так как грань АВ невидима относительно плоскости проекций П2 (рис. 124). Определяем также видимость очерков.
|
|
|
Пересечение кривых поверхностей
Кривые поверхности пересекаются в общем случае по пространственной кривой линии, проекции которой строятся обычно по точкам.
Пример 1. Построить линию пересечения цилиндра и усеченного конуса (рис. 125).
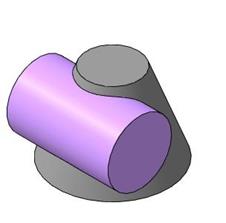

Рис. 125
Две кривые поверхности пересекаются по пространственной кривой.
Цилиндрическая поверхность является фронтально-проецирующей. Следовательно, фронтальная проекция линии пересечения совпадает с фронтальным очерком цилиндра – окружностью. Построим горизонтальную проекцию, исходя из условия принадлежности точек этой линии, поверхности усеченного конуса. Отмечаем характерные точки – фронтальные проекции точек А2 и Т2 на пересечении фронтальных очерков цилиндра и усеченного конуса (рис. 126).
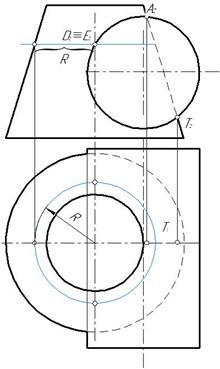

Рис. 126 Рис. 127
Отметим фронтальные проекции M 2, N 2,в которых будет меняться видимость линии пересечения на горизонтальной плоскости проекций. Точки K 2, L 2 – низшие точки линии пересечения. Точки D 2, E 2, G 2 , H 2 – точки изменения видимости на профильной плоскости проекций. В2, С2 – выбраны произвольно на фронтальном очерке цилиндра.
|
|
|
Горизонтальные проекции точек, принадлежащих поверхности усеченного конуса, находим на окружностях соответствующего радиуса. Соединяем полученные точки плавной линией с учетом видимости. Точки, принадлежащие видимой части поверхности цилиндра относительно горизонтальной плоскости проекций, соединяем сплошной линией. В точках М1, N 1 происходит изменение видимости. Определяем видимость горизонтальных и фронтальных очерков цилиндра, и усеченного конуса (рис. 127).
Пример 2. Построить линию пересечения тора с цилиндром (рис. 128).


Рис. 128
Цилиндр занимает горизонтально-проецирующее положение. Горизонтальная проекция линии пересечения совпадает с горизонтальным очерком цилиндра.


Рис. 129 Рис. 130
Фронтальную проекцию линии пересечения находим как линию, принадлежащую тору. Точки А2 и В2 отмечаем на пересечении фронтальных очерков тора и цилиндра (рис. 129).
Для нахождения фронтальной проекции С2 проводим по поверхности тора линию а (а1, а2), которая на фронтальную плоскость проекций спроецируется в виде дуги окружности радиуса R. На этой дуге отмечаем фронтальную проекцию С2 и D 2 (проекция точки D, находящаяся на невидимой части цилиндра). Затем найдем произвольные точки М, N, E, F. Для этого строим на поверхности тора линию b. Фронтальная проекция b 2 – дуга окружности радиуса R 1. Полученные точки соединяем плавной линией (рис. 130). Определяем видимость очерков поверхностей.
|
|
|
Пример 3. Построить линию пересечения сферы с конусом (рис. 131).


Рис. 131
Заданы две поверхности общего вида. У этих поверхностей имеется общая плоскость симметрии, поэтому линия пересечения будет симметрична относительно этой плоскости. Обе поверхности второго порядка, следовательно, линия их пересечения пространственная кривая четвертого порядка.
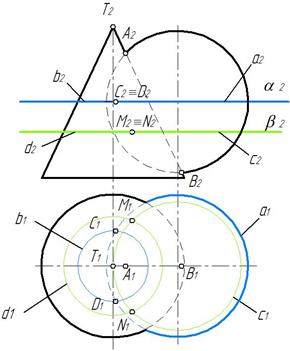
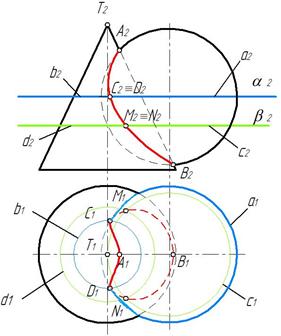
Рис. 132 Рис. 133
Отметим характерные точки линии пересечения. Точки А и В лежат на пересечении фронтальных очерков. Точки С и D находим на пересечении экватора сферы a и окружности b поверхности конуса, лежащих в одной горизонтальной плоскости α. Аналогично находим и другие точки линии пересечения. Так точки М и N строим как пересечение окружностей c и d, принадлежащих одной горизонтальной плоскости β (рис. 132).
|
|
|
Полученные точки соединяем плавной кривой с учетом видимости. При установлении видимости следует помнить, что эта линия будет видима, если она принадлежит как поверхности сферы, так и конуса. Точки А и В отделяют видимую относительно фронтальной плоскости часть линии пересечения (она проходит через точки А, С, М, В) от невидимой. В данной задаче фронтальные проекции видимой и невидимой части линии пересечения совпадают.
Точки С и D отделяют видимую относительно горизонтальной плоскости часть линии пересечения от невидимой. Точка А видима относительно горизонтальной плоскости проекций, так как лежит выше экватора сферы. Следовательно, линия, проходящая через точки А, С, D – видима, остальная часть линии невидима. Определяем видимость очерков поверхности конуса и сферы (рис. 133).
Дата добавления: 2019-09-13; просмотров: 584; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
