Перпендикулярность прямой и плоскости

⇐ ПредыдущаяСтр 16 из 17Следующая ⇒

Из геометрии известно, что прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым, лежащим в этой плоскости (рис.163).

Рис. 163

Если прямые а и b будут прямыми общего положения, то прямой угол к ним ни на одной плоскости проекций не спроецируется в натуральную величину. Согласно теореме о проецировании прямого угла, прямой угол спроецируется в натуральную величину на плоскость проекций, если одна сторона прямого угла будет параллельной этой плоскости проекций. Поэтому, в качестве прямых надо взять горизонталь h и фронталь f. Тогда прямой угол между перпендикуляром n и h спроецируется в натуральную величину на П₁, а прямой угол между n и f – на П₂. На рис. 164 в точке K, принадлежащей плоскости α(а‖b), построен перпендикуляр n к плоскости.

Рис. 164

Пример 1. Из точки А провести перпендикуляр к плоскости и найти его основание (рис. 165).

Прямая m является фронталью, а прямая n – горизонталью. Строим фронтальную проекцию перпендикуляра p перпендикулярно фронтальной проекции фронтали. А горизонтальную проекцию перпендикуляра p проводим перпендикулярно к горизонтальной проекции горизонтали. Символически это можно записать так: р₂^m ₂; p ₁ ^n ₁.

Рис. 165 Рис. 166

Находим основание перпендикуляра. Для этого решаем задачу на пересечение прямой с плоскостью. Через перпендикуляр проводим вспомогательную плоскость β ^П₂.

Затем строим линию пересечения вспомогательной плоскости с заданной, это прямая 1-2. На пересечении перпендикуляра с прямой 1-2 будет искомая точка K (рис. 166).

Пример 2. Через точку А провести плоскость перпендикулярную прямой l (рис. 167).

Рис. 167 Рис. 168

Проводим через точку А фронталь f искомой плоскости так, чтобы f ₂^l ₂. Строим горизонталь так, чтобы h₁^ l ₁. Искомая плоскость определена двумя пересекающимися прямыми α(f∩h) (рис. 168).

Пример 3. Через точку А провести прямую, перпендикулярную плоскости α^П₂ (рис. 169).

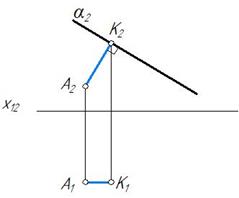
Рис. 169 Рис. 170

Плоскость α фронтально-проецирующая. Строим перпендикуляр к фронтальной проекции плоскости. Горизонтальная проекция перпендикуляра А₁K₁ параллельна оси х₁₂, так как АK является фронталью (рис. 170).

Перпендикулярность плоскостей

Из геометрии известно, что всякая плоскость, проходящая через перпендикуляр к другой плоскости, перпендикулярна этой плоскости. Через заданную точку можно провести бесконечное множество плоскостей, перпендикулярных к данной плоскости. Для этого нужно провести через точку прямую, перпендикулярную к плоскости. Все искомые плоскости пройдут через эту прямую.

Пример 1. Через заданную точку А провести плоскость β, перпендикулярную плоскости α(f∩h) (рис. 171).

Рис. 171 Рис. 172

Через заданную точку А строим прямую m, перпендикулярную заданной плоскости, для этого строим m ₂^f ₂ и m ₁^h ₁. Плоскость зададим двумя пересекающимися прямыми. Вторая прямая n будет, например, профильно-проецирующая. Искомая плоскость β(m∩n). Через точку можно провести бесконечное множество плоскостей, перпендикулярных заданной плоскости (рис. 172).

Пример 2. Через заданную АВ провести плоскость, перпендикулярную α(ΔС DE) (рис. 173).

Если плоскость содержит в себе перпендикуляр к плоскости, то эти плоскости перпендикулярны.

Рис. 173 Рис. 174

Чтобы через прямую АВ провести плоскость надо, например, через точку В провести перпендикуляр к данной плоскости α(ΔС D Е). Сторона С D является фронталью, а сторона СЕ – горизонталью. Проекции перпендикуляра l ₂ и l ₁ проводим соответственно перпендикулярно проекции фронтали и горизонтали данной плоскости. Искомая плоскость определена β(АВ∩l) (рис. 174).

Определение расстояний

Пример 1. Найти длину отрезка АВ (рис. 175).

Рис. 175

Чтобы найти длину отрезка занимающего в пространстве общее положение относительно плоскостей П₁ и П₂, надо построить дополнительную ортогональную проекцию отрезка АВ на плоскость П₄ ему параллельную (П₄‖АВ) и П₄^П₁ (рис. 175).

Поэтапное решение задачи на эпюре показано на рис. 176.

Рис. 176

Пример 2. Построить дополнительную ортогональную проекцию прямой общего положения на плоскость ей перпендикулярную (рис. 177).

Рис. 177

Cтроим дополнительную ортогональную проекцию прямой АВ на плоскость ей параллельную (П₄‖АВ) и П₄^П₁. Ось х₁₄ построена параллельно А₁В₁. Прямая АВ из общего положения переходит в прямую уровня. Затем строим дополнительную ортогональную проекцию прямой АВ на плоскость П₅ ей перпендикулярную (П₅^ АВ) и П₅^П₄. Ось х₄₅ построена перпендикулярно А₄В₄. На плоскости П₅прямая будет точкой. Рещение задачи на эпюре показано на рис. 178.

Рис. 178

Пример 3. Определить расстояние от точки А до прямой l (рис. 179).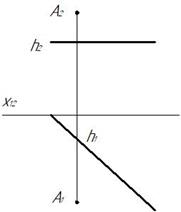

Рис. 179 Рис.180 Рис.181

Расстояние от точки до прямой определяется длиной отрезка перпендикуляра, опущенного из точки на прямую.

На эпюре проекции перпендикуляра к прямой можно построить, если прямая параллельна плоскости проекций. Заданная прямая h является горизонталью, она параллельна плоскости проекций П₁. Поэтому по теореме о проекциях прямого угла опускаем перпендикуляр на горизонтальной плоскости проекций(А₁ K ₁^h ₁) (рис. 180). Отрезок перпендикуляра А K является отрезком общего положения, поэтому найдем его натуральную величину. Для этого построим дополнительную ортогональную проекцию отрезка А K на плоскость П₄, проходящую через него и П₄^П₁ ,на этой плоскости отрезок изобразится в натуральную величину. При этом ось х₁₄ проходит через А₁ K ₁ Отрезок А₄_K₄определяет расстояние от точки А до прямой h (рис. 181).

Пример 4. Определить расстояние между двумя параллельными прямыми m и n (рис. 182).

Перпендикуляр, опущенный из любой точки одной прямой на другую, определяет расстояние между прямыми.

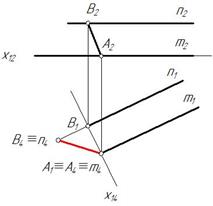
Рис. 182 Рис. 183

Обе параллельные прямые m и n параллельны плоскости П₁. Задаем любую точку А на прямой m и опускаем из этой точки А перпендикуляр на прямую n по теореме о проекциях прямого угла А₁В₁^n ₁. Отрезок АВ является отрезком общего положения. Находим его натуральную величину. Для этого проводим через него плоскость П₄ и П₄^П₁. Новая ось х₁₄ проведена через горизонтальную проекцию А₁В₁. На линиях связи от новой оси х₁₄ откладываем отрезки, равные расстояниям от А₂ и В₂ до оси х₁₂.Расстояние между А₄ и В₄ будет искомым (рис. 183).

Пример 5.Определить расстояние между скрещивающимися прямыми l и m, l^П₁ и m – прямая общего положения (рис. 184).

Под расстоянием между скрещивающимися прямыми понимается длина отрезка перпендикуляра, общего для обеих прямых.

Рис. 184 Рис. 185

Если одна из скрещивающихся прямых lперпендикулярна к плоскости проекций П₁, то их общий перпендикуляр АВ параллелен плоскости проекций П₁. При этом прямой угол между перпендикуляром и прямой m проецируется на плоскости П₁ в прямой угол, и проекция отрезка перпендикуляра А₁В₁ между прямыми l и m определяет расстояние между ними (рис. 185).

Пример 6.Определить расстояние между скрещивающимися прямыми l и m (обе общегоположения) (рис. 186).

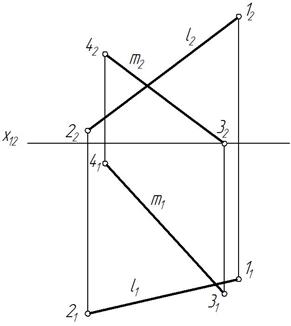
Рис. 186

Расстояние между скрещивающимися прямыми представляет собой длину отрезка, перпендикулярного обеим прямым. В данной задаче обе прямые l иm занимают общее положение, значит необходимо одну из прямых, пусть это будет прямая l, преобразовать в проецирующую.

Рис. 187

Строим дополнительную ортогональную проекцию прямойl (на ней заданы точки 1 и 2) и прямой m (на ней заданы точки 3 и 4) на плоскости П₄, параллельной прямой l и перпендикулярной к П₁ (П₄‖ l и П₄^П₁).При этом осьx ₁₄ параллельна l ₁ (x ₁₄ ‖ l ₁) (рис. 187).

Рис. 188

Рис. 189

Затем строим дополнительную ортогональную проекцию прямойl и прямой m на плоскости П₅, перпендикулярной к прямойl и перпендикулярной к П₄ (П₅^l и П₅^П₄; x ₄₅^ l ₄) (рис. 188).

На плоскости П₅ определяем искомое расстояние между скрещивающимися прямыми l иm, опустив перпендикуляр из точки l ₅ на проекциюm ₅ (M ₅ N ₅^m _5, MN = M ₅ N ₅).

Строим остальные проекции отрезка MN, при этом M ₄ N₄^l ₄ согласно теореме о проекциях прямого угла (рис. 189).

Пример 7. Построить дополнительную ортогональную проекцию плоскости общего положения α(ΔАВС) на плоскости П₄, перпендикулярной к плоскости α и к плоскости П₁.

Из геометрии известно, что две плоскости взаимноперпендикулярны, если одна из них содержит прямую, перпендикулярную другой плоскости. В данном примере перпендикуляром к плоскости П₄ является горизонталь h (рис. 190).

Рис. 190

Исходя из этого, ось х₁₄ проведена перпендикулярно горизонтальной проекции h₁ горизонтали h плоскости ΔАВС (рис. 191). По отношению к плоскости П₄ плоскость ΔАВС является проецирующей и изображается на ней в виде прямой А₄В₄С₄.

Рис. 191

Пример 8. Определить расстояние от точки М до плоскости α(ΔАВС) (рис. 192).

Рис. 192 Рис. 193

Расстоянием от точки до плоскости является длина отрезка перпендикуляра, опущенного из точки на плоскость.

Заданная плоскость α занимает горизонтально-проецирующее положение. Проводим горизонтальную проекцию М₁K₁ под прямым углом к А₁В₁С₁. Фронтальная проекция перпендикуляра М₂K₂ проводим параллельно оси х₁₂, так как отрезок МK параллелен плоскости проекций П₁. Отрезок М₁K₁ есть искомое расстояние от точки М до плоскости α (рис. 193).

Пример 9. Определить расстояние от точки А до плоскости α(ΔВС D) (рис. 194).

Рис. 194

Если плоскость является проецирующей, то перпендикуляр к ней параллелен плоскости проекций и длина проекции его отрезка на этой плоскости проекций равна искомому расстоянию. Заданная плоскость α является плоскостью общего положения. Преобразуем ее в частное положение. Для этого построим дополнительную ортогональную проекцию плоскости α и точки А на плоскости, перпендикулярной к плоскости α и к плоскости П₁.

Рис. 195

Плоскость П₄ будет перпендикулярна к плоскости α, если она перпендикулярна к горизонтали этой плоскости. При этом ось х₁₄ перпендикулярна к горизонтальной проекции h ₁ горизонтали h плоскости α. Дополнительной ортогональной проекцией плоскости α на плоскость П₄ является прямая B ₄ C ₄ D ₄ (рис. 195)

Из точки А₄опускаем перпендикуляр А₄ K ₄ на прямую B ₄ C ₄ D ₄ . Длина отрезка А₄ K ₄ равна расстоянию от точки А до плоскости α(ΔBCD). Строим проекции отрезка АK. Горизонтальная проекция А₁K ₁ параллельна оси х₁₄, так как отрезок АK параллелен плоскости П₄, и перпендикулярна к горизонтальной проекции h ₁ горизонтали h плоскости α. Фронтальную проекцию K ₂ точки K строим по двум ее проекциям K ₁ и K ₄ (рис. 196).

Рис. 196

На основании решения рассмотренной задачи можно определить расстояние между параллельными прямой и плоскостью, между двумя параллельными плоскостями.

Пример 10. Определить расстояние от точки А до плоскости α(h∩f ) (рис. 197).

Рис. 197

Преобразуем плоскость α(h∩f) из общего положения в проецирующее. Для этого необходимо построить дополнительную ортогональную проекцию плоскостиα(h∩f) на плоскость ей перпендикулярную. При этом дополнительная плоскость проекций П₄ должна быть одновременно перпендикулярна и к плоскости α, и к одной из двух исходных плоскостей проекций, например, плоскости П₁, т. е. П₄^α и П₄^П₁. На эпюре это условие соблюдается в том, что осьx₁₄ проведена перпендикулярно к горизонтальной проекцииh ₁ горизонталиh плоскостиα, что следует из того, что плоскостьП₄ будет перпендикулярна к плоскости α, если она перпендикулярна к горизонтали этой плоскости. Дополнительной ортогональной проекцией плоскости α на плоскостьП₄является прямая линияα₄. Точка 1 отмечена произвольно на фронтали f (рис. 198).

Рис. 198 Рис. 199

Затем строим дополнительную ортогональную проекциюА₄ точкиА на плоскость П₄и из точки А₄ опускаем перпендикуляр на прямую α₄. Длина отрезка А₄ K ₄ равна искомому расстоянию от точки А до плоскости α(h∩f),т. е. А₄ K ₄ =А K. Горизонтальная проекция А₁ K ₁ параллельна осиx₁₄, так как отрезок А K параллелен плоскости П₄, и перпендикулярна к горизонтальной проекцииh₁ горизонталиh плоскости α. Фронтальная проекцияА₂ K ₂построена перпендикулярно f₂(рис. 199).

Пример 11. Определить расстояние между прямой EF и плоскостью α(ABCD) ей параллельной (рис. 200).

Рис. 200

Расстояние измеряется длиной перпендикуляра, опущенного из произвольной точки, принадлежащей прямой Е F на плоскость ей параллельную. Таким образом, задача сводится к задаче на определение расстояния от точки до плоскости. В данном примере прямая А D является горизонталью плоскости, поэтому для преобразования плоскости α(ABCD) из общего положения в частное ось х₁₄ строим перпендикулярно h ₁. Плоскость П₄^α(ABCD) и П₄^П₁. Плоскость спроецируется в прямую. Затем из произвольной точки М₄, принадлежащей прямой Е₄ F ₄, проводим перпендикуляр М₄ N ₄ на дополнительную проекцию плоскости. Отрезок М₄ N ₄ – есть искомое расстояние между прямой и параллельной плоскостью.

Рис. 201

Построены также фронтальная и горизонтальная проекции этого расстояния (рис. 201).

Пример 12. В точке А провести перпендикуляр к плоскости α(ΔАВС) длиной 25 мм (рис. 202).

Рис. 202

Прямая АВ является фронталью, а прямая АС – горизонталью. Строим p₂^А₂В₂ и p ₁^А₁С₁. Перпендикуляр p – это прямая общего положения (рис. 203). Чтобы отложить на перпендикуляре отрезок 25 мм отметим на нем произвольную точку 1. Строим дополнительную ортогональную проекцию отрезка А1 на плоскость, проходящую через него и П₄^П₁^. На П₄ отрезок спроецируется в натуральную величину. Отложим от А₄ 25 мм, получим K₄. Потом строим K₁ и K₂ (рис. 204).

Рис. 203 Рис. 204

Пример 13. Опрелелить размеры треугольника АВС, перпендикулярного горизонтальной плоскости проекций П₁ (рис. 205).

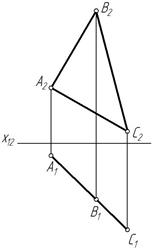
Рис. 205 Рис. 206

Для определения размеров треугольника (натуральной величины) надо построить его дополнительную ортогональную проекцию на плоскость ему паралельную. Для этого плоскость П₄‖ΔАВС и П₄^П₁. Новую ось х₁₄ проводим параллельно А₁В₁С₁. Измерим расстояние от фронтальных проекций точек до оси х₁₂ и отложим его на плоскости П₄ от оси х₁₄. Дополнительная проекция А₄В₄С₄ является натуральной величиной ΔАВС (рис. 206).

Пример 14. Определить размеры треугольника АВС (рис. 207).

Рис. 207

Чтобы найти величину ΔАВС, являющегося плоскостью общего положения, надо построить его дополнительную ортогональную проекцию на плоскость ему параллельную. Для этого надо сначала построить дополнительную ортогональную проекцию плоскости общего положения α(ΔАВС) на плоскости П₄, перпендикулярной к плоскости α(ΔАВС) и к плоскости П₁ (см. пример). А затем построить его дополнительную ортогональную проекцию на плоскость П₅ ему параллельную (П₅‖ΔАВС) и П₅^П₄ (рис. 207). Решение задачи на эпюре показано на рис. 208.

Рис. 208

Определение углов

Истинную величину угла, истинную величину плоской фигуры можно определять способом вращения вокруг линии уровня (горизонтали или фронтали). Этот способ используется для преобразования плоскости общего положения в плоскость уровня.

Линия уровня, вокруг которой поворачивается плоскость общего положения, должна принадлежать этой плоскости. В этом случае поворот плоскости сводится к повороту только одной точки, не принадлежащей оси вращения.

Рассмотрим процесс совмещения точки В с горизонтальной плоскостью Δ путем вращения ее вокруг горизонталиh, принадлежащей этой плоскости (рис. 209).

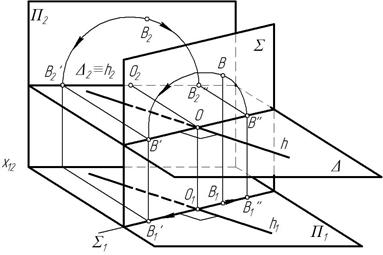
Рис. 209

Точка В, вращаясь вокруг горизонталиh, будет описывать окружность, расположенную в плоскости Σ^h. Центр О этой окружности является точкой пересечения оси вращения h с плоскостьюΣ. Радиус окружности равен расстоянию от точки В до осиh(R_В= OB).

Так как плоскостьΣ перпендикулярнаh, аh параллельна П₁, то Σ перпендикулярна П₁, ее горизонтальная проекция изображается прямойΣ_1┴h₁. Следовательно, окружность, описываемая точкой В, будет проецироваться на плоскостьП₁ в отрезок прямой, совпадающий с прямойΣ₁. Проекцией этой окружности на плоскостьП₂ будет эллипс, так как плоскостиΣ иП₂ не параллельны.

Таким образом, при вращении точки В вокруг горизонтали ее горизонтальная проекцияВ₁ перемещается по прямой Σ₁^h ₁. Направление перемещения зависит от направления вращения точки В (на рис. 209 показано стрелками). В то время, когда точка В совместится с плоскостьюΔ и займет одно из положений В′ или В″, ее горизонтальная проекцияВ₁, переместившись по прямойΣ₁, соответственно займет положение В₁′ илиВ₁″.

Рис. 210

На эпюре (рис. 210) построения выполняются в следующей последовательности:

1) через горизонтальную проекциюВ₁ точкиВ проводим перпендикуляр к горизонтальной проекцииh₁ горизонталиh – оси вращения точки В;

2) определяем проекции О₁ и О₂ точки О – центра вращения точки В вокруг горизонталиh;

3) находим длину отрезка OB – радиуса вращения точки В вокруг горизонталиh методом дополнительного ортогонального проецирования OB = O ₄ B ₄ = R_В;

4) из точкиО₁, как из центра, описываем окружность радиусаR_В и отмечаем точкиВ₁′ и В₁″пересечения ее с прямойΣ₁;

5) точкиВ₁′ и В₁″являются горизонтальными проекциями соответственно точек В′ и В″, фронтальные проекцииВ₂′ и В₂″ определяем по линиям связи на прямой h ₂.

В случае поворота точки вокруг фронтали и совмещения ее с фронтальной плоскостью уровня рассуждения аналогичны.

Пример 1. Определить угол между пересекающимися прямыми l и m. Задачу решить вращением вокруг горизонтали (рис. 211).

Рис. 211

Отмечаем в плоскости a(l ⋂ m) горизонталь h и поворачиваем плоскость вокруг горизонтали h в положение горизонтальной плоскости. При этом точки 1 и 2, принадлежащие горизонтали, остаются неподвижными. Точка А перемещается по окружности, плоскость которой перпендикулярна к горизонтали. На плоскость П₁ окружность проецируется в отрезок прямой, перпендикулярной к горизонтальной проекции h ₁ горизонтали h. Проводим через горизонтальную проекцию А₁ точки А прямую, перпендикулярную к h₁, и отмечаем точку О₁, в которой она пересекает h ₁. Точка О₁ – горизонтальная проекция центра О окружности, по которой перемещается точка А. Его фронтальная проекция О₂ принадлежит h ₂. Отрезки О₁A₁ и О₂А₂ – горизонтальная и фронтальная проекции радиуса R_A указанной окружности. Отрезок ОА является отрезком общего положения.

Рис. 212

Находим длину радиуса R_A, для чего строим дополнительную ортогональную проекции О₄А₄ отрезка ОА на плоскости П₄, проведенный через отрезок ОА и перпендикулярной к П₁. Отложив отрезок О₄А₄ на прямой О₁А₁ и от точки О₁, находим горизонтальную проекцию А¢₁ точки А после поворота. Соединив точку А¢₁ с точками 1₁ и 2₁, получаем проекции l¢₁ и m¢₁ прямых l и m после поворота. Угол j между ними равен искомому углу (рис. 212).

Угол между скрещивающимися прямыми равен углу между пересекающимися прямыми проведенными параллельно заданным скрещивающимся.

Пример 2. Определить угол между плоскостями a(а ⋂ b) и β(с ⋂ d) (рис. 213).

Рис. 213

Угол между двумя плоскостями равен углу между перпендикулярами к этим плоскостям.

Из произвольной точки пространства K (K₁, K₂) проводим перпендикуляры t (t ₁^a ₁, t ₂^b ₂) к плоскости a(а⋂b) и q(q ₁^c ₁_, q ₂^d ₂) к плоскости β(с⋂d) (рис. 214).

Рис. 214

Плоскость перпендикуляров t и q поворачиваем вокруг фронтали f(f₁, f₂) до положения фронтальной плоскости. Фронтальные проекции t¢₂ и q¢₂повернутых перпендикуляров t и q образуют угол j, равный искомому углу между двумя плоскостями a и β (рис. 215).

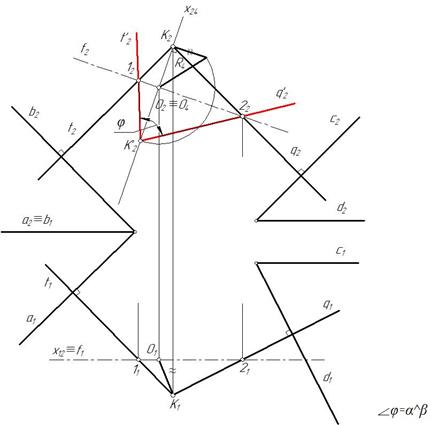
Рис. 215

Величину угла между перпендикулярами можно найти способом дополнительного ортогонального проецирования (рис. 216).

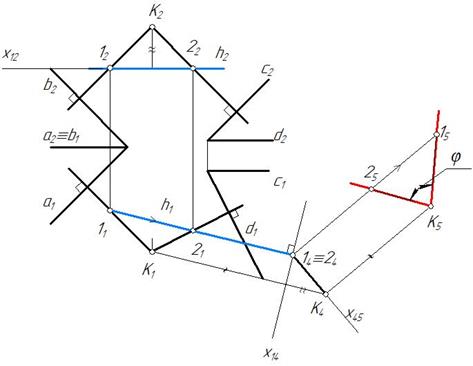
Рис. 216

Пример 3. Определить угол между прямой l и плоскостью a(h ⋂ f) (рис. 217).

Рис. 217

Углом между прямой и плоскостью является угол между этой прямой и её ортогональной проекцией на эту плоскость. Исходя из этого, решение задачи может быть следующим. Из произвольной точки М прямой l опускаем перпендикуляр n на плоскости a. Находим точку пересечения этого перпендикуляра с плоскостью (точка М_a) и точку K пересечения прямой l с плоскостью a. Через точки K и М_a проводим прямую l_a – проекцию прямой l на плоскости a. Угол j между прямыми l и l_a – искомый угол.

Решение задачи упрощается, если определить угол ω (угол между прямой l и перпендикуляром n). Зная угол ω, определим искомый угол j = 90°– ω. Для построения перпендикуляра n, на эпюре n ₁ строится перпендикулярно к h ₁, а n ₂ строится перпендикулярно к f ₂ (рис. 218).

Рис. 218

Угол ω между прямой l и перпендикуляром определяется поворотом плоскости этого угла вокруг горизонтали h*. Угол j получается дополнением угла ω до 90°(рис. 219).

Рис. 219

Пример 4. Определить угол наклона плоскости α(а‖b) к горизонтальной плоскости проекций (рис. 220).

Рис. 220 Рис. 221

Для определения угла наклона плоскости общего положения α(а‖b) к горизонтальной плоскости проекций необходимо преобразовать ее в плоскость частного положения перпендикулярную дополнительной плоскости проекций П₄^П₁. Плоскость П₄должна также быть перпендикулярна плоскости α(а‖b). Из геометрии известно, что две плоскости взаимно перпендикулярны, если одна из них содержит прямую перпендикулярную к другой плоскости. На основании этого проводим в плоскости α(а‖b) горизонталь h и перпендикулярно h ₁ построим ось x ₁₄. Строим дополнительную ортогональную проекцию горизонтали h ₄, которая спроецируется в точку. Затем строим дополнительную проекцию произвольной точки А, принадлежащей плоскости α. Через точки А₄ и h ₄ проходит дополнительная проекция плоскости α₄. Угол наклона φ между осью х₁₄ и α₄ есть искомый угол наклона плоскости α к горизонтальной плоскости проекций (рис. 221).

Пример 5. Определить величину двугранного угла между пересекающимися плоскостями АВС и АВD (рис. 222).

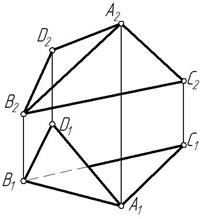
Рис. 222

Углу между двумя плоскостями соответствует линейный угол между прямыми, по которым данные плоскости пересекаются третьей плоскостью, перпендикулярной к линии их пересечения.

Линия пересечения ΔАВС и ΔАВD известна, это прямая АВ. Прямая АВ –общего положения. Строим дополнительную ортогональную проекцию этой прямой на плоскость ей параллельную: П₄‖АВ и П₄^П₁. Ось х₁₄ проводим параллельно А₁В₁, ось х₁₂ проводим через В₂ (рис. 223). Строим дополнительные проекции остальных точек.

Рис. 223

Затем строим дополнительную проекцию прямой АВ на плоскость ей перпендикулярную: П₅^АВ и П₅^П₄. Для этого ось х₄₅проводим перпендикулярно А₄В₄. Прямая АВ спроецируется в точку на плоскости П₅, а пересекающиеся плоскости в прямые линии. Линейный угол φ – искомый угол между плоскостями (рис. 224).

Рис. 224

Пример 6. Определить истинную величину треугольника. Задачу решить вращением вокруг линии уровня (рис. 225).

Рис. 225

Повернем плоскость треугольника вокруг горизонтали так, чтобы она стала параллельна горизонтальной плоскости проекций. Тогда треугольник на эту плоскость изобразится в истинную величину.

Проводим горизонталь h через точку А, так как точки расположенные на оси вращения остаются неподвижными. Поворачиваться будут вершины треугольника С и В. Повернем точку С вокруг горизонтали h .

Точка С будет поворачиваться в плоскости δ^h (δ₁^h ₁) по окружности радиуса ОС. Радиус ОС является отрезком общего положения. Определяем его истинную величину. Для этого строим плоскость П₄ через ОС и П₄^П₁. Положение осей х₁₂ и х₁₄ показано на рис. 226.

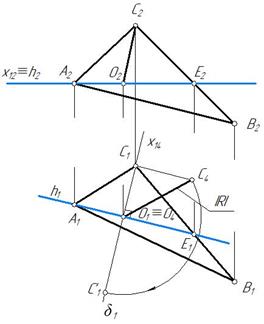
Рис. 226 Рис. 227

Отрезок О₄С₄ – истинная величина отрезка ОС. Полученную истинную величину откладываем в плоскости δ и получим повернутое положение точки С–С ' ₁.

Рис. 228

Точка В поворачивается в плоскости γ^П₁(γ₁^h ₁). Находить истинную величину радиуса вращения ОВ нет необходимости. Проводим через неподвижную горизонтальную проекцию Е₁ неподвижной точки Е прямуюС ' ₁ Е₁ и в пересечении с плоскостью γ(γ₁) отмечаем повернутое положение точки В-В ' ₁. Соединяем полученные точки В ' ₁ и С ' ₁ с неподвижной вершиной А ' ₁(рис. 228).

Эта проекция и определяет истинную величину ∆АВС. Фронтальная проекция треугольника окажется преобразованной в прямую, которая совпадает с фронтальной проекцией горизонтали.

Дата добавления: 2019-09-13; просмотров: 845; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 8 9 10 11 12 13 14 151617 Следующая ⇒

Мы поможем в написании ваших работ!