Р абота при адиабатном изменении объема газа
Найдем выражение для работы, совершаемой газом в адиабатном процессе. Запишем первый закон термодинамики для адиабатного процесса 
, так как 
тогда
.
Знак минус означает, что если газ адиабатно расширяется от объёма V1 до V2, то его температура падает от Т1 до Т2. Чтобы получить полную работу, надо проинтегрировать последнее выражение вдоль процесса перехода газа из состояния 1 в состояние 2.
|
Согласно формуле Майера и коэффициента Пуассона:
.
Подставим в (6.3.1) или с учетом уравнения 
и уравнения Менделеева – Клапейрона 
.
.
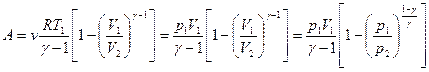Сравним работы, совершаемые газом в адиабатическом и изотермическом процессах при одном и том изменении объема от V1 до V2. Это сравнение удобнее всего провести графически (рис. 6.3.1).
Исходное состояние газа одинаковое – точка 1. Из графика видно, что работа расширения газа от V1 до V2 (заштрихованная площадь под кривыми) больше работы расширения газа в изотермическом процессе – она совершается за счет получения энергии извне. В адиабатическом процессе нет притока энергии извне – работа расширения газа совершается за счет изменения внутренней энергии.
При адиабатическом сжатии работа, совершаемая внешними силами, оказывается больше чем работа при изотермическом сжатии. Следовательно, выгоднее сжимать газ изотермически.
П олитропические процессы
Практические процессы не носят строго адиабатического или строго изотермического характера, т.к. невозможно осуществить ни полной термической изоляции, ни идеального обмена теплом. Реальные процессы носят характер средний между изотермическим и адиабатическим, они относятся к более общим политропическим процессам.
|
|
|
Политропическими называются процессы, при которых теплоемкость тела С остается постоянной.
Найдем уравнение политропы для идеального газа (вывод аналогичен выводу уравнения адиабаты). Для этого напишем уравнение первого начала термодинамики, подставив значения
и 
;
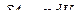. (6.4.1)
Далее запишем уравнение состояния:
,
дифференцирование которого дает:
,
откуда
.
Подставив это значение dT в уравнение (6.4.1) и произведя приведение подобных членов, получим
.
Поскольку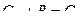 
, разделив обе части последнего выражения на произведение р V, придем к дифференциальному уравнению:
.
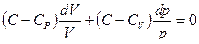В случае если 
, то, разделив на 
, получим
.
Обозначим через 
, получим 
.
Так как для данного газа n = const, то после интегрирования получим
;
Потенцируя, получим
.
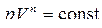Это уравнение – есть искомое уравнение политропы идеального газа. Величина n называется показателем политропы.
|
|
|
Решив уравнение 
относительно С, получим формулу для теплоемкости идеального газа при политропическом процессе:
.
Все рассмотренные ранее процессы являются частными случаями политропического процесса в зависимости от значения показателя политропы n. При n = 1 уравнение 
дает 
, т.е. уравнение изотермического процесса.
Согласно выражению подстановка n = 1 дает значение 
. Это объясняется тем, что в изотермическом процессе 
, тогда как 
.
При 
дает уравнение адиабатического процесса 
, а выражение 
обращается в нуль 
. Действительно, теплоемкость идеального газа при адиабатическом процессе равна нулю, так как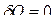 
, в то время как 
.
При n = 0 из уравнения политропы получаем р = const, а это условие изобарного процесса, и из формулы получаем, что C = CP.
И, наконец, рассмотрим случай 
. Извлекая корень n–й степени из общих частей уравнения политропы, получаем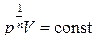 
. Т.к. 
, то получаем V = const, т.е. условие изохорического процесса, тогда из формулы получаем, что C = CV.
Можно опытным путем определить значение показателя политропы n и установить, к какому процессу близок данный реальный процесс.
Для этого по экспериментальной зависимости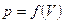 
определяют значения параметров 
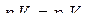для двух произвольных точек; составляют уравнение:
|
|
|
,
откуда находят n:
.
Лекция 7
Дата добавления: 2019-09-13; просмотров: 447; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!