С корость, ускорение и энергия
Гармонического колебания
Определим скорость гармонического колебания. Для этого продифференцируем уравнение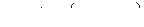 
по времени. После выполнения дифференцирования, получаем
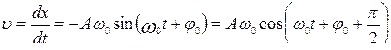. (9.2.1)
Таким образом, скорость маятника тоже изменяется по гармоническому закону, но по фазе опережает смещение х на угол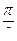 
.
Это видно на рис. 9.2.1, где приведены графики смещения и скорости.
Продифференцировав последнее выражение еще раз по времени, найдем выражение для ускорения:
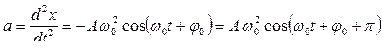. (9.2.2)
Рис. 9.2.1
Из последнего выражения видно, что ускорение а и смещение х находятся в противофазе (рис. 9.2.1).
Амплитуды скорости и ускорения соответственно:
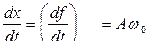; (9.2.3)
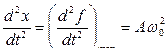. (9.2.4)
Фаза скорости отличается от фазы величины смещения на 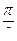, а фаза ускорения отличается от фазы величины x на p, т.е. меняется в противофазе. Следовательно, в момент времени, когда x = 0, скорость 
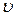приобретает наибольшее значение, когда же смещение x достигает максимального отрицательного значения, то ускорение 
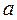приобретает наибольшее положительное значение.
Определим, как изменится во времени потенциальная и кинетическая энергия маятника. Потенциальная энергия измеряется работой внешних сил, которая совершена для того, чтобы вызвать определенное смещение x.
dА = F × dx ; F = -kx; dА = -kxdx.
|
|
|
Полная работа определяется интегрированием:
.
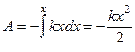Работа совершается за счет уменьшения потенциальной энергии:
; 
.
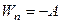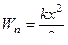Подставив в эту формулу значение х из (9.1.5) получаем
.
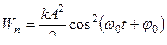Для вычисления кинетической энергии воспользуемся формулой
.
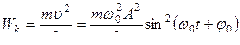Учитывая, что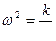 
, можно записать
.
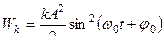Полная энергия колеблющейся системы в любой момент времени оказывается постоянной:
.
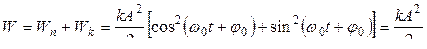Таким образом, полная энергия колеблющейся системы прямо пропорциональна квадрату амплитуды колебания и не зависит от времени.
Можно показать, что среднее значение:
.
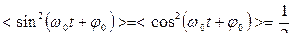Действительно, графики функций синуса и косинуса отличаются лишь сдвигом по фазе, вследствие чего их средние значения должны быть равны. Из равенства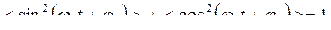 
следует, что их средние значения равны ½. Используя это соотношение, получаем
.
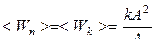Таким образом, при гармонических колебаниях средние по времени значения потенциальной и кинетической энергий равны друг другу.
Полная энергия незатухающего гармонического колебания:
.
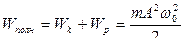Из последних формул следует, что Wk и Wp изменяются с частотой 2w 0, т.е. частотой, которая в два раза превышает частоту собственных колебаний (рис. 9.2.2).
В то же время, когда Wp максимальна (в положении наибольшего отклонения х = А) Wk = 0 и наоборот в положении равновесия (х = 0) Wp = 0, а Wk – максимальна.
|
|
|
Т.к.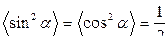 
, то из последних формул вытекает, что
.
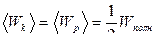Если полная энергия гармонического колебания не зависит от времени (W = const), то такие колебания называются незатухающими.
Полная энергия гармонического колебательного движения прямопропорциональна квадрату амплитуды и квадрату частоты колебания и не зависит от времени.
Итак: гармонические колебания, возникающие в системе, устойчивы и продолжаются сколь угодно долго, если на систему не действуют внешние силы и в системе отсутствуют силы трения и другие, которые могли бы привести к рассеянию энергии.
Лекция 10
Дата добавления: 2019-09-13; просмотров: 196; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!